例談多元變量最值問題求解策略*

四川省成都市第十八中學 (610072) 向 城 安 邦內江師范學院數學與信息科學學院 (641100) 劉成龍

多元變量(二元或以上)的最值(范圍)問題是中學數學教學的難點，同時是高考、自主招生、數學競賽命題的熱點.如何應對該類問題呢？我們認為減元是核心.而減元過程中選取恰當的工具或策略是非常關鍵的.研究表明，重要不等式法、待定系數法、三角換元法、幾何意義法、先猜后證法等在解決多元變量最值(范圍)問題上有強大的功能，文中以2019年高考、自主招生和競賽中的多元變量最值(范圍)問題為例加以說明.

策略1重要不等式法

點評:當條件中出現和為定值，而又不能直接運用基本不等式時，可考慮運用“1”的代換，構造出滿足運用基本不等式的條件，達到減元目的.

分析:利用平面幾何知識，將ΔBDF的面積用題目中的x，y，z表示出來，問題就轉化為求三元函數的最大值.

圖1

點評:得到目標函數為三元函數，觀察可發現x出現兩次，y，z各出現一次，且結合已知條件有y+z=1+x，利用二元基本不等式消元將三元函數轉化為一元函數，此處利用三元基本不等式整體消元得到最大值，也可從函數角度求得最大值.

例3 (2019年全國卷Ⅰ理科23題)已知a，b，c是正數，且abc=1.證明:

(Ⅱ)(a+b)3+(b+c)3+(c+a)3≥24.

(Ⅱ)因為a，b，c是正數，且abc=1，故有(a+b)3+(b+c)3+(c+a)3≥3·

策略2待定系數法

分析:目標函數為三元齊次式，呈現的是積與平方和之間的關系，考慮用待定系數法將平方和轉化為“積”的形式.

解析:顯然xy+2yz>0時才能取得最大值.設x2+y2+z2=(x2+λy2)+[(1-λ)y2+z2]≥

策略3三角換元法

分析:可行域x2+(y-2)2≤1表示的是一個圓盤，考慮用三角換元.

策略4幾何意義法

例7 (2019年全國卷Ⅲ理科23題)設x，y，z∈R，且x+y+z=1.

(Ⅰ)求(x-1)2+(y+1)2+(z+1)2的最小值；

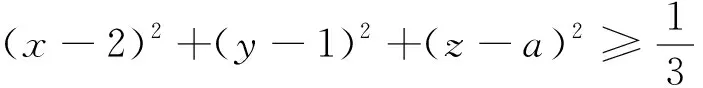
策略5先猜后證法

評析：牛頓說：“沒有大膽的猜想，就沒有偉大的發現”．波利亞說：“先猜后證——這是大多數的發現之道”．本例正是通過猜想，得到了λ的最大值，將原問題轉化為了證明一個具體的結論，實現了問題的簡化.

人的智慧取決于元認知能力.心理學研究表明，反思和總結是開發元認知的有效途徑.因此，反思和總結不僅能幫助教師進行高效的教學，也能有助于激活學生的數學直覺思維、邏輯思維、發散思維、創新思維等.同時，注意總結也是單墫教授提出的12條解題要訣之一.文中正是通過對多元變量最值(范圍)問題的求解策略進行總結和反思，以期讀者對這一類問題有深刻認識.