微專題在中考數學復習中的應用

陳晚珍

摘要：微專題復習具有“因微而準、因微而細、因微而深”的特點，不僅更加具有針對性，還可以有效鍛煉學生的思維能力，尤其是對于中考的數學復習而言，由于數學難度的增加很多學生都會呈現出厭學的狀態，而微專題復習教學手段的運用就不同了，既可以提高學生的學習效率，又可以讓知識得到深度的拓展。為此，本文就微專題在中考數學復習中的應用價值和策略進行了探究分析。

關鍵詞：微專題;中考數學復習;應用

中圖分類號：G633.6 ???????????文獻標識碼：A文章編號：1992-7711（2020）10-019-1

“微專題”是指立足學情、教情、考情，選擇一些切口較小、角度新、針對性強的復習專題進行學習，可以單獨研究的知識體系，或者某種數學思想方法，根據學生不同學習階段具有一定彈性，又稱“小專題”;“微專題”教學是指針對某一具體知識點，從該知識的基本概念、基本原理、基本規律入手，內化知識，構建結構進行知識遷移，整合并運用基本概念和原理解決實際問題的一種“小切口”教學方法。它可以鞏固學生學習基礎知識的同時，幫助學生形成良好的認知結構，活化知識的運用。對于中考而言，微專題復習手段的運用既縮小了學生的學習范圍，又能讓學生的復習更加具有針對性。

一、微專題在中考數學復習中的價值

專題復習可以說是教師教學、學生復習階段的重要組成部分，而微專題的利用更是學生數學學習能力提升的有效途徑：

第一，微專題的復習范圍相對專題復習而言比較小，這也就說明學生在進行數學知識系統學習的時候更加具有針對性，同時也有利于學生結合數學知識進行學習計劃的制定，在提升學生學習效率的同時加深學生對數學知識的理解能力。

第二，微專題的復習方法可以將重難點進行有效凸出。這樣可以避免學生盲目學習，在重難點顯現的過程中使得學生對數學復習有一個科學的學習過程，在進行知識搭建的時候進行重點復習、難點鞏固，最終使得學生達到舉一反三的學習效果。

由此可見，微專題在中考復習中的運用價值所在。為此，教師一定要重視微專題的教學模式。通過教學內容、教學模式的創新，使得學生在微專題的復習中得到數學學習能力的綜合提升。

二、微專題在中考數學復習中的運用策略

1.利用微專題，立足學情教育提高學生的復習水平

在初三數學教學中，作為學生學習、教師教學的重要階段，采用微專題進行中考數學復習，教師就要結合學生的學習情況，在了解學生整體水平的過程中實現學生數學復習學習興趣的激發。例如，教師以“一元一次方程”作為微專題進行復習的時候，可以結合層次遞進的復習模式，例如，教師可以利用回眸教材知識：以等式的性質、一元一次方程的概念和性質為引導，然后結合中考考向為學生展示以下微專題：

例1：某商店若將某型號彩電按照標價的八折出售，則此時每臺彩電的利潤為5%，已知該型號彩電的進價為4000元，求該型號彩電的標價

例2：某種商品每件的標價是330元，按照標價的八折銷售仍然可獲利10%，則這種商品的每件進價為（ ）

A 240元? B 250元? C 280元? D 300元

在微專題的設置、層次性的引導以及知識變形分析，使得學生在復習階段得到思維能力的鍛煉。

2.利用微專題，整合教學內容鍛煉學生的復習思維

微專題復習方法的運用，是為了讓學生在學習知識的時候可以探索到學習技巧，進行基礎知識夯實、重難點鞏固。為此，教師可以利用教學內容進行整體分析，通過教材的研讀，使得微專題的設置更加科學化。例如，在復習“一次函數及其圖像”這一內容時，可以凝練以下復習題型：

例1：已知一次函數y=（3a+2）x-（4-b），問實數a、b取何值時，使得：

（1）y隨x的增大而減小;

（2）圖像經過二、三、四象限;

（3）圖像與y軸的焦點在x軸上方;

（4）圖像經過原點。

例2：在直角坐標系內，直線y=kx+b經過三點，A（2，0）B（0，2） C（m，3）求：

（1）求這條直線的函數解析式;

（2）求m的值和AC的長度;

（3）求∠OCA的正弦值。

在這一微專題中，可以明顯看出例1考察了一次函數的定義、圖像和性質等基礎知識，而例2 既考察了函數解析式，也考驗了學生數形結合的思維，同時還結合了三角函數的知識點，不僅讓知識更加具有綜合性，還有效鍛煉了學生的數學綜合能力。

3.利用微專題，創優教學理念提高學生的復習質量

在利用微專題的時候，教師不僅要讓學生得到數學知識的掌握，還要讓學生得到數學能力的培養。在教學理念的創新中實現復習質量的提升，利用微專題讓學生進行復習評價、學習檢測。例如，在復習“解決函數最值問題”這一數學內容時，教師可以為學生開展這一微專題訓練，如：

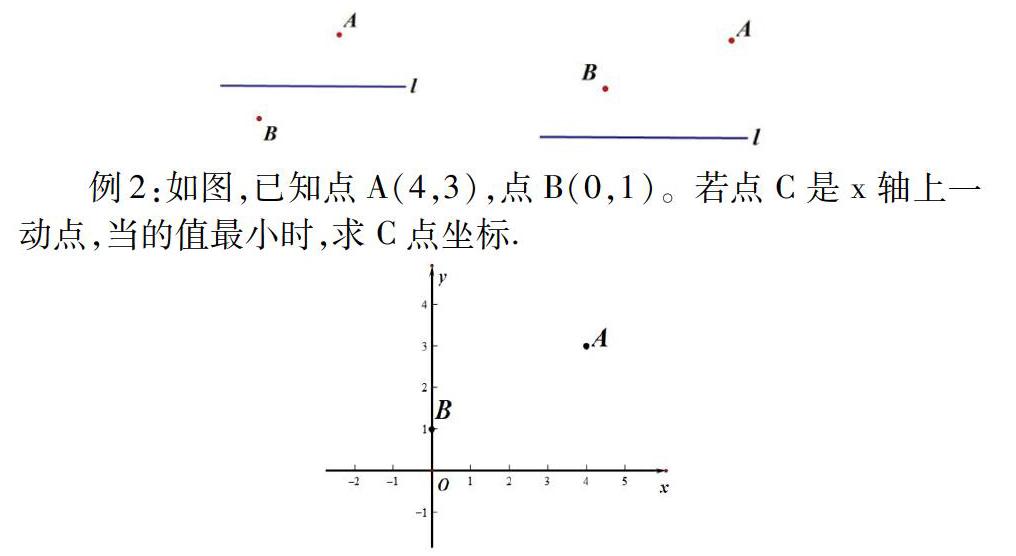
例1：如圖，要在燃氣管道l上修建一個泵站，分別向A，B兩城鎮供氣.泵站修在什么地方，可使所用的輸氣管線最短？

例2：如圖，已知點A（4，3），點B（0，1）。若點C是x軸上一動點，當的值最小時，求C點坐標.

在微專題的解一次函數最值問題的設置中，通過由點（動點）定線（對稱軸）→定對稱點→求解析式→求動點坐標的一個復習學習過程中，使得學生的解題思路得到優化，從而發揮微專題的育人價值，提高學生的數學復習質量。

三、結語

利用微專題進行中考數學復習，教師要做到科學設置，讓每一個例題都具有針對性、教育性，從而使得學生在微專題的學習中得到數學思維能力、數學解題能力、數學理解能力得到綜合能力的提升，使得中考數學復習教學得到教學水平和教學質量的共同發展。

[參考文獻]

[1]朱炎芳.微專題在中考數學復習中的應用[J].數理化解題研究，2019（29）.

[2]顧大權.數學教學中“微專題”復習的開展與運用[J].教學與管理，2018（31）：56-58.

（作者單位：桂林市平樂縣平樂中學，廣西 桂林 542400）