兒童空間觀念的發展策略

杭菁

摘 要：“空間觀念”作為新課標十個核心概念之一，高度凸顯了其內涵特征和價值，兒童空間觀念的培養需要我們重新考查衡量圖形幾何教學的實質，讓學生形成獨特的思維方式。本文從作圖教學、聯結遷移兩個方面，對兒童空間觀念的發展策略展開闡述。

關鍵詞：空間觀念 發展策略

在幾何課程中，空間觀念被認為是數學能力中的重要部分，兒童空間觀念的發展，對于幫助他們理解、解釋和欣賞我們現實的幾何世界是十分關鍵的，也能為今后進一步系統學習幾何知識打下良好的基礎。下文從兩個方面對兒童空間觀念的發展策略展開闡述。

一、作圖教學：鋪好空間觀念發展的奠基石

美國數學家斯蒂思曾指出，如果一個特定的問題可以轉化為一個圖形，那么就整體地把握了問題，并且能創造性地思考問題的解法。因此，學會作圖是學生的空間觀念、解決問題能力得以發展的基本途徑 ，我們要幫助學生建立“畫圖是一種發現問題、分析問題、解決問題的策略”的意識，將作圖教學貫穿始終，使學生形成用圖說話，用圖推理，用圖解決問題的良好習慣。

1.培養讀圖能力

縱觀教材我們可以發現圖文并茂是一大特點，無論是例題還是練習的設計，都需要學生去閱讀、發現、理解圖中隱含的線索，因此，提高學生的讀圖能力刻不容緩。

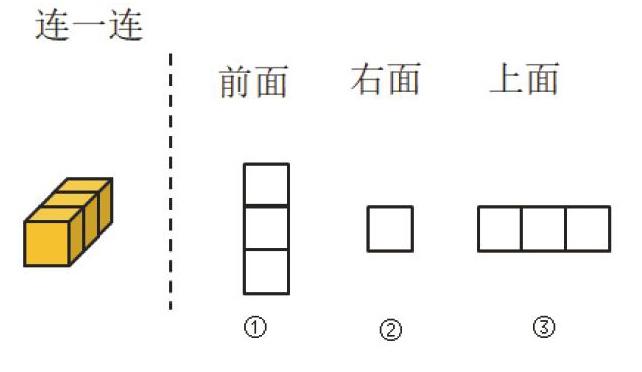
如：《觀察物體》中的習題

教學中應引導學生觀察：①和③雖然都是三個正方形，但由于方向不同，①是豎著的，③是橫著的，因此①是從上面看到的形狀，而③是從右面看到的形狀。

小學生的思維模式，以感性思維比較多，也是向抽象思維過渡的一個階段，這個階段可以以讀圖為起點，配合實物或者模型操作，圖形結合、化虛為實，給學生帶來真實、豐盈的感知，積累大量的表象，建立起圖像與立體圖形的空間聯系，形成“空間知覺”。

2.示范作圖方法

兒童模仿能力強，他們的作圖習慣、作圖方法、作圖能力往往是從教師的作圖示范中模仿學來的。因此，教師的言傳身教極為

重要。

例如在教授畫一定長度的線段時，教師應一邊示范，一邊講解：先確定線段的一個端點，再將直尺的0刻度線對齊這個端點，再從左往右根據線段長度確定另一個端點并畫出線段。雖然這些內容看起來很細小，但卻是學生作圖能力后續發展的基礎。

3.體會作圖價值

要讓學生心甘情愿作圖，那就首先要讓學生體會作圖價值：圖形特點越畫越鮮明，數量關系越畫越清晰，思維越畫越順暢，思考越畫越深入。激發了學生運用作圖解決問題的意識，他們才會產生作圖的意愿。

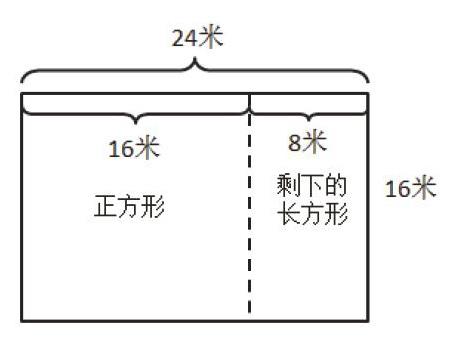
以《長方形的周長》一課中的習題為例：一塊長方形木板，長24米，寬16米，鋸下一個最大的正方形，正方形的周長是多少米？剩下木板的周長是多少？這一題如果讓學生想象，空間思維好的學生能想象出來，但對于基礎較差，空間思維較薄弱的孩子來說肯定有一定難度，如果畫畫圖，這道題的難度就大大降低了。

這張圖將鋸下的正方形和剩下的長方形特征直觀表現出來，文字信息縮減了，卻更明了了，既能幫助孩子解題，又能讓孩子在想象的基礎上將所想表達出來。有了這樣的成功體驗，相信學生會更愿意畫圖。

二、聯結遷移：降低空間觀念發展的難度

蘇教版教材注重對各個板塊內容之間的銜接，各個知識點前后都有關聯。如果將看起來分散的知識點編織成一張知識網，形成知識的點上開放、線上關聯、整體建構，可使兒童的思維向長度、深度和廣度延展，那將大大降低空間發展觀念的難度。

1.知識聯結

在教學中，教師應引領兒童理清知識的來龍去脈，整體、系統、聯系地把握知識的結構，達到同類知識在兒童知識體系中自然生長的狀態。

比如，以《多邊形的面積》教學為例，長方形、正方形、平行四邊形、三角形、梯形等平面圖形的公式，如果將它們看作獨立內容，那么學生要記憶的是五個又難記又易混淆的公式，這對本就有記憶障礙的孩子來說無疑雪上加霜。其實它們看似獨立實則關聯。

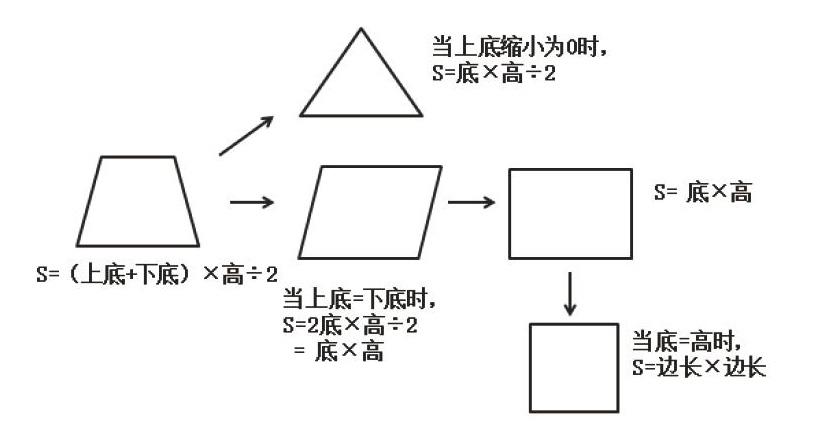
如果以梯形的面積計算公式為中心，向外發散：把梯形的上底縮小為0，成為一個三角形，三角形的面積=底×高÷2;如果上下底變成一樣長，就變成了平行四邊形或長方形，平行四邊形（長方形）=底×高;如果將底和高變成一樣長，就是一個正方形，正方形面積=邊長×邊長。如此，一個公式關聯著四個公式，降低了記憶難度，也能讓學生知道圖形之間的關系。

看來，知識聯結可以化多為少，化繁為簡，降低空間觀念的發展難度。

2.方法聯結

在知識學習過程中，方法遷移能正向指引學生在遇到新問題時的思考方向。

比如，在“圖形和幾何”這一部分內容中，“轉化”策略貫穿前后，不管是推導平面圖形的面積：平行四邊形轉化成長方形、三角形（梯形）轉化成平行四邊形、圓轉化成長方形……還是推導立體圖形的體積：圓柱轉化成長方體……都會發現是“轉化”這種思想起著鏈接的橋梁作用。

在教學中經常會發現，只要題目稍稍一變，有的學生就不會做了，究其原因就是思維的斷鏈：就題論題，沒有想到題目不同，但思想方法是相通的。看來，小學數學教學中思想方法的滲透是必然與要求，提煉和感悟數學思想方法是發展空間觀念的精神橋梁。

總之，空間觀念的培養和提高，不是“一朝一夕，一招一式”之事。在教學中，我們應根據教學目標、教學內容合理選擇教學手段和方法，更有效地促進學生數學素養的發展。