高中階段面向計算思維的編程教學模式的實踐與思考
賈金元 武小龍
摘? 要 闡述計算思維的內涵,對面向計算思維的高中編程培養教學模式及教學案例進行分析,給出面向計算思維的高中編程培養路徑;通過讓學生了解和掌握編程知識和基本的C++語言算法,提高學生的信息素養,有效培養學生的計算思維。
關鍵詞 計算思維;C++;編程教學;信息技術;校本課程;任務驅動
中圖分類號:G632? ? 文獻標識碼:B
文章編號:1671-489X(2020)03-0106-03
1 前言
隨著大數據時代的到來,計算思維作為一種解決問題、設計系統、理解人類行為的綜合思維模式,受到社會各界的關注,對計算思維的培養和探索也成為當前基礎教育關注的熱點。教育部發布的《關于全面深化課程改革 落實立德樹人根本任務的意見》指出,信息網絡技術突飛猛進,時代和社會發展需要進一步提高國民的綜合素質,培養創新人才[1]。從教育部在2018年頒布的信息技術新課程標準中可以看到,信息技術課程從內容上已大幅減少基本軟件的教授,而是緊跟信息技術的發展,提出要培養學生的信息意識、計算思維、數字化學習與創新及信息社會責任,同時開設人工智能、開源硬件、3D打印等選修課程。
在高中階段開展編程教育,培養計算思維,在各大重點高中相對比較受重視,這從每年參加NOIP的人數和進入國家集訓隊的數量上就可以看出來。高中階段學習C++語言,基本是以校本課程的形式存在,學生大部分是準備去參加信息學競賽。目前市面上的教材可大體分為兩類:一類是專門供程序員學習的語法參考書,教授程序設計思想;另一類是側重于信息學競賽的教材。大部分所選編程實例用于語法規則的驗證和偏重于數學知識方面,兩者之間沒有很好地銜接。高中生由于數學基礎較薄弱,往往吃不透、用不活,知道語法規則但是無法解決問題,究其原因是教學過程中不關注計算思維的培養。
基于此,筆者提出在高中開設編程課程,一方面可以教給學生基礎程序設計語言的語法知識,另一方面可幫助學生提高算法設計能力。
2 相關概念
計算思維? 2006年,美國卡內基·梅隆大學的周以真教授在Communications of the ACM雜志上首次提出計算思維的概念。他認為計算思維是運用計算機科學的基礎概念,求解問題、設計系統和理解人類行為的一系列思維活動,其本質是抽象和自動化[2]。2012年,美國麻省理工學院媒體實驗室提出計算思維的三維框架,包括計算概念、計算實踐和計算觀念三個維度,引發了計算思維實踐層面的研究和評價[3]。因此,高中階段對學有余力的學生進行C++編程教學,具體要從培養學生問題求解思路、創新思維和對問題的形式化描述上入手。
編程教學? 為什么要選擇C++作為編程教學的語言?因為C++語言更接近于底層,語法雖然比較復雜,但對于已初步具備高階思維的高中生而言,C++學習可以為將來以后的語言(Python、Java等)學習打下良好的基礎;通過編程教學,逐步領會算法在程序設計中的重要作用。培養學生計算思維的目的是讓學生養成以計算思維的角度來思考并解決問題,可以采用多種方式培養學生的計算思維能力。
在傳統的教學模式中,教師會先講授基本語法,然后讓學生通過上機進行相關知識點的練習;學生往往感到學習難度較大,難以入門,甚至導致喪失學習的積極性,不利于培養自主學習和自主思維能力。用計算思維的理念重新審視編程教學,利用現有的課程,讓學生掌握程序設計背后蘊含的計算思維。編程教學的最終目的是讓學生掌握解決現實生活中真實問題的方法,編程能力則是計算思維和能力運用的綜合體現。
3 面向計算思維的高中編程教學模式及教學案例分析
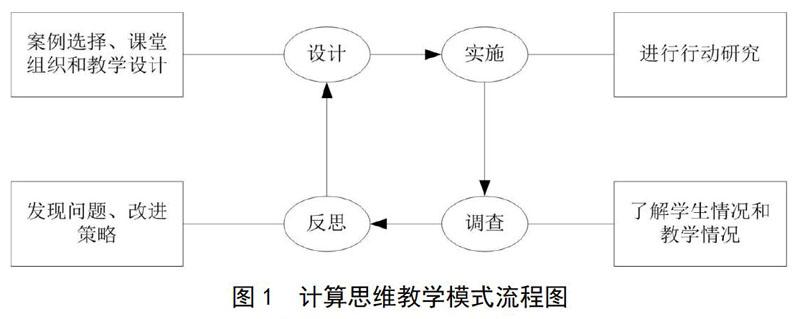
計算思維教學模式流程圖如圖1所示。面向計算思維的高中編程教學模式的教學流程及任務設計主要包括課堂教學環節及各環節教學任務設計兩部分。高中階段開設C++校本課程,對訓練學生計算思維很有幫助。在教學過程中,通過設計案例,采用任務驅動式教學方法,讓學生發現問
題;在講授的時候把算法與計算思維緊密結合起來,給學生講清楚實際問題中蘊含的計算思維及算法。比如利用棧的數據結構來處理車廂調度問題,利用弗洛伊德算法解決最短路徑問題等,把計算思維融入解決實際生活問題的過程中,讓學生不再是從理論上學習,而是更多地將注意力集中在分解問題和解決問題的過程中,并結合數學學科知識如數論、圖論等進行學習。
教學內容? C++程序中的for語句和while語句。
教學目標? 了解循環的概念,理解為什么循環是編程中的一種重要控制結構;學習如何使用C++中的for和while語句來編寫循環,以及每一個語句類型的使用時機,掌握常用的循環模式;找出循環規律并設計算法,利用循環語句解決實際程序問題,進一步訓練邏輯思維、計算思維能力。
教學設計
1)課程導入。帶領學生回顧上一節課學習的選擇結構程序設計,在猜商品價格的游戲案例中,利用if語句實現判斷猜測數字是大了、小了還是對了,和學生一起,邊講邊寫出利用if語句的猜數字程序。但是程序只能猜一次就結束,如果想重復猜測該數字,直到猜對價格為止,用程序如何實現呢?
2)介紹循環的概念,循環其實就是需要有限次重復執行的程序段,如日夜更迭、四季交替等大自然中的循環。以操場上一圈一圈跑步為例,引導學生寫出程序(略)。
3)分步點評學生寫出的程序,分析for語句循環示例,找出循環的規律和要素。
4)重點講解while語句的語法結構,讓學生明白,編寫循環語句,類似做填空題,要把循環要素填到相應的位置。在程序演示環境下,逐步找出循環體,結合while語句語法,寫出下面程序,設置while的循環條件為空,讓學生來填:
#include
using namespace std;
int main()
{
int truePrice,caiPrice=0,i=0;
cout<<”請輸入一個數,這個數字是商品的真實價格”< cin>>truePrice; cout<<”請輸入你猜的數”< while(讓學生來填) { i++; cout<<”參與者”; cin>>caiPrice; if(caiPrice>truePrice) { cout<<”大了”< } else if(caiPrice { cout<<”小了”< } else { cout<<”恭喜你,猜對了,共猜了”< endl; } } return 0; } 通過猜商品價格,可以激發學生的學習興趣,讓他們有種躍躍欲試的感覺,最終得出答案,循環條件是:truePrice!=caiPrice。 5)引導反思:如果每人最多可以猜7次,超過就算輸,如何修改程序? 4 面向計算思維的高中編程培養路徑 創設情境,分層教學? 在教學過程中,針對有些比較難掌握的概念,教師可以創設情境、分層教學。比如有個關于循環語句的訓練題:假設所有的燈都是關著的,編號為1的人走過來,把是1的倍數的燈全部打開;編號為2的人把是2的倍數的燈全部關上;編號為3的人又把是3的倍數的燈開的關上,關的開起來……直到第N個人為止。現在問:如果給定一個數N,那么在N輪之后,還有哪些燈是開著的? 這樣的題目讓很多學生感到無從下手,因為如果N是個位數,還可以手動算,教師可以讓10個學生手拉手排成一排,模擬這個算法的運行。編號為i的燈只會被它的約數所操作,而它最后是開著的,所以說一定被操作了奇數次。只有一個數是完全平方數,其約數才是奇數,所以只要輸出i到N中的完全平方數就可以。通過這樣的教學,部分學習程度較好的學生已經可以寫出來,然后讓這幾個學生講解一下算法,全班進行點評。 加大對實驗程序調試的指導力度? 編程教學最重要的是能夠上機并調試出正確的程序。因此,要指導學生切勿眼高手低,在剛開始學習的時候一定要多上機,只有通過上機,才能發現問題。比如對于小數點位數的輸出,C和C++輸出語句不同,都可能導致程序調試不通過。因此,對實驗內容進行分組,設立基本組、提高組,利用一些在線OJ網站,讓學生多做題。一方面,教師可以實時觀察到學生的進度;另一方面,這些網站上有相應的題解,學生可以實時進行對比和分析。 思維風暴,多種解題方法匯聚? 問題的解決方法有多種,筆者在教學中發現,對于同一個題目,往往有很多種算法可以實現。比如“最大公約數”的問題,就有枚舉法、輾轉相除法、輾轉相減法等多種解法。通過一題多解,可以開拓學生思路,引導學生積極進行算法求解,使學生印象深刻,豁然開朗。 創新課堂教學? 每個學生都是學習的主人。筆者所在的班級每周都有一個學生課堂,就是學生選擇一個自己學習過的最拿手的算法進行講解。這樣既促進了學生對算法的理解,也加深了其他學生的認識,在講授的過程中還可以發現問題。比如遞歸算法的基本思想是什么?實際上就是把規模大的、難解決的問題變成規模小的、容易解決的同一問題,規模較小的問題又變成規模更小的問題,當問題小到一定程度時,可以直接得出它的解,從而得到原來問題的解。 5 結語 “人工智能+教育”時代背景下,計算思維的重要性日益凸顯。如何在信息技術教學中培養學生的計算思維,使學生具備數字化時代的創新素養,是信息技術教師面臨的重大課題。本文就在高中開設C++編程教學的特點和目前普遍存在的問題展開論述,提出把計算思維融入整個教學環節,通過實際教學,效果良好。在高中開展面向計算思維的編程教學,可以為高中生提供一個與大學課程銜接的機會,也可以進一步推動信息技術與課程教學的深度融合。因此,在高中階段推廣編程教學、研究編程教育意義重大。 參考文獻 [1]教育部關于全面深化課程改革 落實立德樹人根本任務的意見[EB/OL].http://old.moe.gov.cn/publicfiles/business/htmlfiles/moe/s7054/201404/167226.html. [2]Wing J M. Computational Thinking[J].Communicationsof the ACM,2006(3):33-35. [3]Brennan K, Resnick M. New frameworks for studying and assessing the development of computational thin-king[M]//Vancouver, Canada: Proceedings of the 2012 Annual Meeting of the American Educational Research Association.2012:1-25.

