數學教學改革實踐案例探討

陳彩華

摘要：為轉變學生的學習方式，圍繞“學為中心”的教學觀，踐行睿智數學教學主張，文章結合教學實踐，對一次函數的一個最值問題進行了拓展與應用研究。文章從一個問題、兩種解法、三類變式、四點思考四方面展開分析，對學生發現問題和分析問題能力的培養做了嘗試。

關鍵詞：教學改革 函數 最值問題

通過圖表，使學生能從中觀察審視函數，有利于更好地認識函數，提高學生對一次函數斜率的幾何直觀認識。“沒有思路就沒有出路”，培養學生解決問題的過程實質上在于引導他們找出解決問題的有效方式與方法，使學生能從動態與靜態角度來觀察審視函數，這有利于學生更好地認識函數。

一、問題

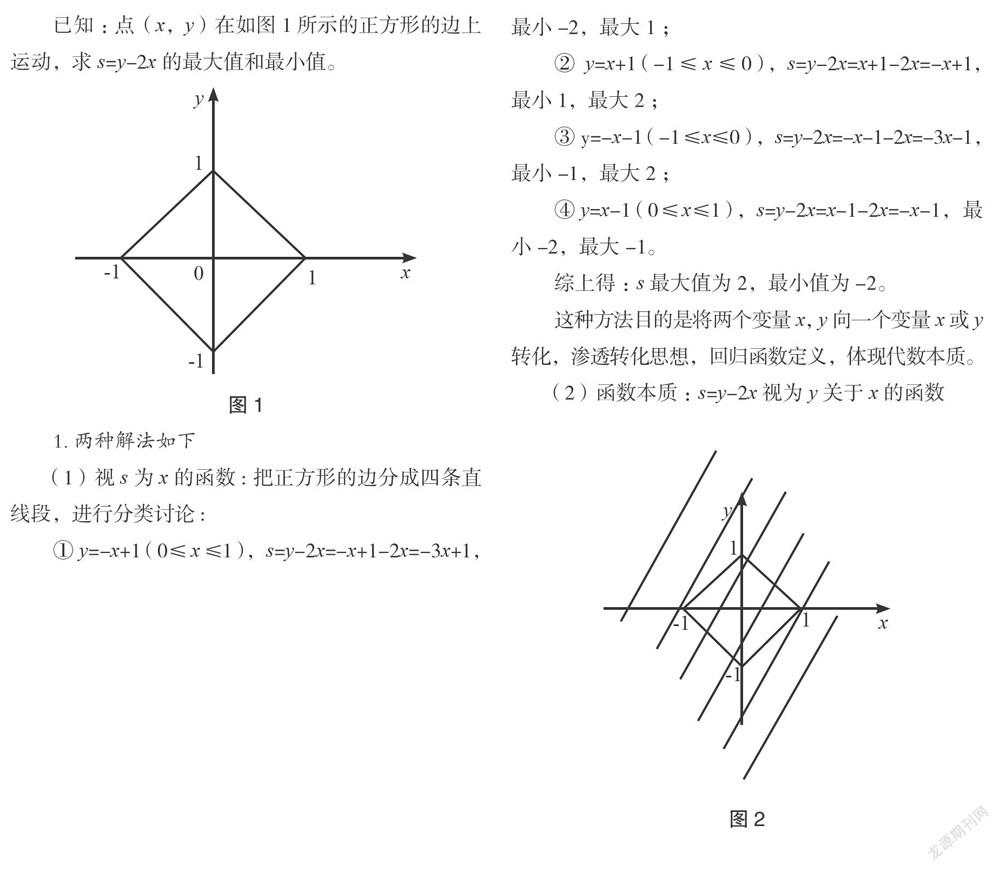
已知：點（x，y）在如圖1所示的正方形的邊上運動，求s=y-2x的最大值和最小值。

旨在激發學生換位思考，讓學生明白任何一個代數式子的背后往往有它的幾何意義存在。

如果我們暫時將s當作常數來認識，那么s在一次函數中起到截距的作用。現在我們又讓它還原本色，s是一個可變化的截距，看會在什么范圍內變化。

這種方法旨在滲透數形結合思想，強化數型結合，讓學生感受s變化的規律，體悟代數式背后的幾何意義。

對于y=kx+b，當k不變時，與6對應的所有直線都相互平行。所以我們通過畫圖可以看出，當直線y=2x+s經過點（-1，0），（1，0）時，相應的截距分別達到最大值和最小值（如圖2）。所以我們直接將點（-1，0），（1，0）代入直線y=2x+s解析式，就可以求得s的最大值與最小值。

2.二類變式如下

（1）變式一

讓學生能通過改變點（x，y）的路徑，編制一個類似的問題。

學生提供的問題：

①點（x，y）在菱形的邊上運動，求s=y-2x的最大值和最小值。

（其他學生還補充了平行四邊形、矩形）

②點（x，y）在等腰梯形的邊上運動，求s=y-3x的最大值和最小值。

③點（x，y）在線段上運動，求s=y-x的最大值和最小值。

④把線段改成雙曲線段，其余不變。

⑤把線段改成拋物線段，其余不變。

⑥把線段改成圓，其余不變。

（針對學生可能對端值上取到最大值或最小值存在誤區，筆者又設置了兩個問題）

（2）變式二

教師給一個問題引領：

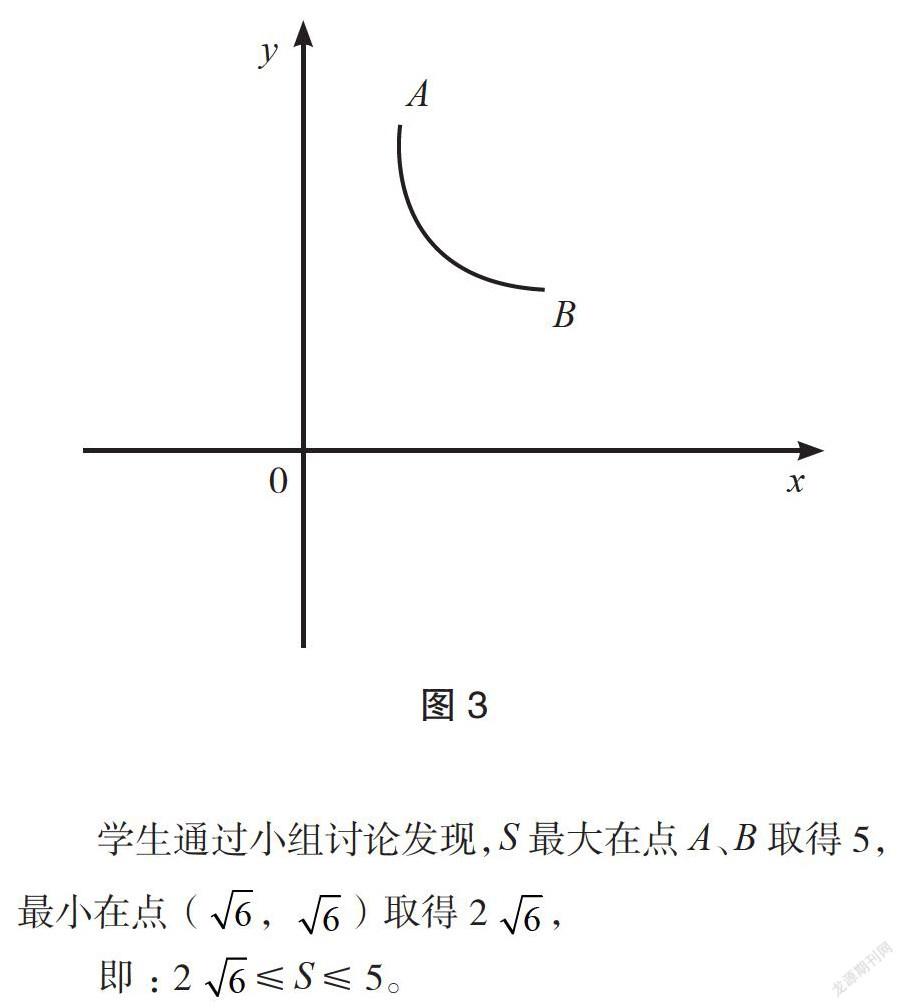
點（x，y）在如圖3所示的雙曲線段上運動，其中A（2，3），B（3，2），求s=y+x的最大值和最小值。

學生討論給出類似問題：

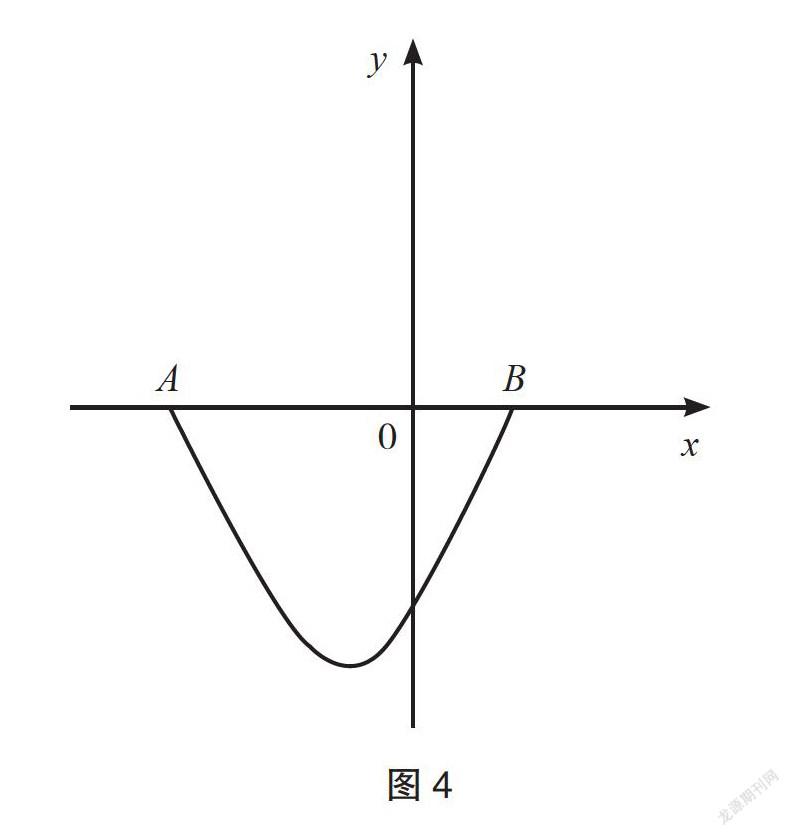
①點（x，y）在如圖4所示的拋物線段上運動，其中A（-3，0），B（1，0），拋物線段頂點縱坐標為-4，求s=y+2x的最大值和最小值。

學生通過小組討論發現，S最大在點B取得2，最小在點（-2，-3）取得-7，

即：-7≤S≤2。

提出問題：你能歸納出何時一定在端點取得最值，何時有最值不在端點取得嗎？

②點在線段上運動時，最值在端點取得，點在曲線上運動時往往有一個最值通常不在端點上。

教師說明：其實學生提出來的點在圓上運動與雙曲線、拋物線一樣可求，待我們到高中進一步學習。

設計意圖：讓學生對端值取值的情況重新做了認識，點在曲線上運動時，端值未必取到最值。

歸納：這類問題通常有兩種解法：一是代數方法：化歸函數，即已知自變量范圍，求函數的取值范圍或最值;二是幾何方法，即經過換位思考，視s為截距，轉化為在給定條件下求s的取值范圍或最值。

二、四點思考

教育家陶行知說過：“創造始于問題，有了問題才會思考，有了思考，才有解決問題的方法，才有找到獨立思路的可能。”通過對案例實踐的反思，筆者認為培養學生發現問題和分析問題的能力可以從以下四方面著手：

1.引導學生重視數學思想，掌握思維方法

案例中學生的回答就是根據式子和圖形的特點，運用分類討論的思想和轉化思想，對問題有初步的思考方法。將s與兩個變量x，y的關系轉化為s與x或者s與y的一次函數關系，回歸函數定義，為問題的解決提供關鍵性的一步。

數學思想在人的實踐活動中產生，并且成為人們認識世界和改造世界極為重要的工具，是問題解決的靈魂。所以要培養學生用數學思想方法去分析、思考、發現，這樣解決問題更有針對性和實效性。

2.引導學生善編善變，促進靈活多變

案例中，當學生回答完畢后，筆者有意識地讓學生自己編題，目標是改變點（x，y）的路徑，編制類似的問題，使學生對問題的本質有更深刻的理解，實現做一題懂一類的目的，大大提高學習效率。

所以讓學生自己參與問題的設計，或改變條件，或改變結論，從而更好地挖掘問題的生長點，獲得問題解決的通性通法，可以促進學生發現問題、分析問題和解決問題能力的進一步提升。

3.引導學生換位思考，突破思維定式

平時教學中，我們可以有意識地適當調整視角，使問題中的元素進行“角色換位”，讓學生從不同角度審視問題，實現已知與未知、常量與變量、相等與不等、特殊與一般、局部與整體、數式與圖形、運動與靜止等的轉換，突破思維定式，獲得新的解決問題的思路和方法。換位思考也有利于教學內容的深化和延伸，有利于培養學生的探究意識和創新能力。

4.給學生創造自主發揮的機會

在“學為中心”教學理念指引下，在案例最后筆者設計學生自己編題一環，方向是s為定值、k可變的一類題型，并由學生自己解答，完成后進行小組交流共享。根據學生的學習能力等情況，成立合作小組，把學習主動權交給學生，讓學生互相合作交流，在自主環境中有更多時間和空間盡情暢想。

三、總結

在培養學生問題分析能力的過程中，我們應該努力做到“六讓”：特征讓學生觀察，思路讓學生探索，方法讓學生尋找，意義讓學生概括，結論讓學生驗證，規律讓學生發現。只有這樣，學生的數學思維能力才會不斷得到強化，從而有效發現問題并解決問題，逐漸接近數學問題發現、分析與思考的最高境界。