怎樣使學生初步形成建模思想




【學科難點解讀】
方程、不等式和函數都是人們刻畫客觀世界的重要數學模型。結合一元一次方程、一元一次不等式、二元一次方程組與一次函數之間的關系,構建完整的知識網絡,培養學生數學建模的思想,是此學段的難點所在。
用建模的思想看一元一次方程,使學生不僅能加深對方程的理解,提高認識問題的水平,還能借用數形結合的思想分析和解釋“一維”空間中出現的比較復雜的變化過程。如何構建對應的圖形闡釋數量關系是學生學習數學的一個難點,也是數形結合思想形成的重要階段。這一類問題基本上要經歷以下幾個環節:⑴建立研究問題的平臺(如恰當的幾何圖形、平面直角坐標系等);⑵確立數與形之間的對應關系;⑶結合圖形的特點尋求相應的數量關系;⑷探索解決問題的合理途徑。通過多角度、多途徑解決同一類數學問題,體現出數學建模的靈活性。
案例:動態演繹、靜態結合──在一元一次方程應用的行程問題中利用數形結合的思想建構數學模型闡釋數量關系
【教學設計及說明】
在列代數式和解一元一次方程的基礎上,本節課的內容是以行程問題中的追及問題、相遇問題為依托,體現一題多解、多題歸一,形成知識的鏈式結構,不僅使學生明白知識本身的內涵,也要清楚知識的外延。繼絕對值后又一次體會數軸上點與數的對應及其位置間的關系,為平面直角坐標系及函數的學習做以鋪設;將算術、方程和函數三者統一起來,體會數學知識生成的必然性。
教學活動以“畫線段圖”為主線,以實現將復雜的數量關系變得直觀明了;通過用“點與點的位置關系”展現行程問題中的數量關系,初步形成數形結合的思想,培養簡單的表達能力,使數學知識簡單化。由學生在直線(或線段)上設計“線段圖”,展現行程問題中路程間的數量關系;在數軸上設計“線段圖”,展現這個動點的運動路徑,實現把抽象的思維變成一種直觀的判斷,實現從實際問題抽象到數學模型的課堂設計。本節課借助變式教學,對數學內容進行不同角度、不同背景的變式,以凸顯問題的本質特征,揭示不同知識點間的內在聯系,使一題多用,多題重組,常給人以新鮮感,以點帶面促使其產生主動參與的動力,使學生由學會,變為會學、樂學。
【微課實錄】
師:直線上有無數個點,是否可以利用直線上“點與點的位置關系”形象的展現行程問題中路程間的數量關系呢?我們不妨通過下面的問題作一個探究性的嘗試,這是一個回聲定位問題。
問題一:
例1.汽車以72千米/小時的速度在公路上行駛,開向寂靜的山谷,駕駛員按一下喇叭,4s后聽到回聲,已知空氣中聲音的傳播速度以340米/秒。求這時汽車離山谷多遠?
師:請同學們根據題意。畫出線段圖,并尋求數量關系。哪位同學能板演?
生:學生的示意圖:設聽到回聲時汽車到山谷的距離是x米
師:總結:通過剛才的探究,我們發現根據線段的大小比較能夠清晰地呈現路程之間的數量關系,也就是可以把抽象的思維變為一種直觀的判斷。
師:同時我們也關注到:在速度一定時,隨時間的變化,有的點相對于定點的位置發生了變化,也就是這個點到定點的距離隨時間的變化而變化,這就是所謂的動點問題,接下來我們研究一個純數學的動點問題。
問題二:
例2.如圖,線段AB的長為24cm,M、N兩點分別從A、B兩點同時出發,在線段AB上運動,點M由點A運動到點B,速度為1cm/s,點N在點M與點B之間做循環往返運動,速度為2cm/s.
(1)求M、N兩點第一次相遇時的時間.
(2)求當M、N兩點第二次相遇時與A點的距離.
師:通過讀題,請分析M、N究竟做了怎樣的運動?
生:點M、N先做相向而行,共同完成全程24cm,實現了第一次相遇。然后點M繼續前行,因為點N比點M的速度快,此時點N返回至點B的途中他們不會相遇,直至點N調頭才再次和點M相遇。
師:現在你了解N點嗎?那么你能演繹N點嗎?哪位同學能演繹M點呢?
(學生演繹腳本:先關注兩點的運動地點、方向和速度。M同學從A走向B的同時,N同學也從B走向A,在此過程中第一次遇到了M同學,相遇后立即調頭返回到B的過程中N的速度大于M的速度,所以N先到B處后,再調頭迎向M同學直至第二次相遇)
請同學們根據他們的演繹,在練習本上畫線段圖,請借助線段間的大小比較,尋求數量關系。(學生的示意圖)
師:總結:利用數形結合的思想,構建數學模型,可以培養我們簡單的表達能力,使數學知識簡單化。
師:我們知道對于數軸,任給一個數,可以確定一個點的位置,反之,一個位置確定的點,不僅能描述它與其他點之間的距離,還能刻畫一個數的大小。讓我們借助一維數軸,解決動點問題。
問題三:
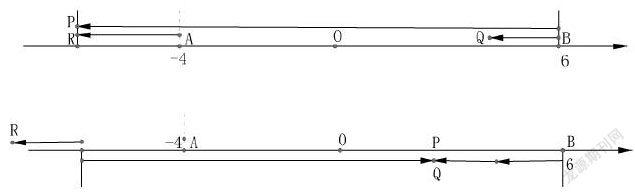
例3.如圖,已知數軸上點A表示的數為6,B是數軸上一點,且AB=10.動點P從點A出發,以每秒6個單位長度的速度沿數軸向左勻速運動,設運動時間為t(t>0)秒.
動點Q從點A出發,以每秒1個單位長度的速度沿數軸向左勻速運動;動點R從點B出發,以每秒個單位長度的速度沿數軸向左勻速運動,若P、Q、R三動點同時出發,當點P遇到點R時,立即返回向點Q運動,遇到點Q后則停止運動.那么點P從開始運動到停止運動,行駛的路程是多少個單位長度?
師:此題信息較多,誰能概括一下它的已知條件。
生:一個定長,三個動點。
師:三個動點是怎么運動的?
生:P、Q同時同地出發,P、R同時異地出發,P追上R后再調頭和Q相遇。
師:現在哪些同學了解了P、Q、R三點?請三位同學真實的再現運動的狀態。
(學生演繹腳本:場景一──整體展示三個點的運動節奏;場景二──片段演繹P、Q和P、R,清晰的呈現追及、相遇的情境)
師:通過如此演繹,主次分明,其中內在的數量關系輕松可以得出。
生:(學生板演示意圖,并講解其中線段間的數量關系。)
師:總結:本節課由靜態圖形到動態圖形,由常量到變量,在思維上有了質的飛躍,為將來的學習創設了條件。
【教學亮點評析】
變化是數學的主要特征,無論是式的變形,還是圖形的變換,都要在變化過程中探究其中的變化規律,判斷相關數量的生成或改變的原因是衡量圖形變化規律的一個重要指標。
本節課為學生創設一個思維發散的空間和知識遷移的途徑,把數形結合的思想巧妙地滲透在探索解決問題方法的過程之中,同時在數學方法的生成、提練的每一個環節中呈現出數形結合的魅力。教學目標是明確的,教學內容是彈性的,學生的思考方向是可選擇的。充分發揮學生的主觀能動性,展現他們的想象力,對于動態與靜態的對立統一的關系有了初步的認識,為最終形成空間觀念和函數思想作了很好的鋪墊。
作者簡介:謝園春(1977-4-22)女,漢族,吉林長春人,碩士學歷,吉林大學附屬中學,教師,數學專業

