基于人工神經網絡的水廠建設項目造價估算方法

王 祺，周 律,*，馬可可，孫 傅，陳宇敏，徐藝星，黃新麗

(1.清華大學環境學院，北京 100084；2.成都環境投資集團有限公司，四川成都 610041)

隨著我國城鎮化建設要求的不斷提高，作為基礎設施的自來水廠工程建設項目新建和改造任務十分艱巨。為提高水廠項目的建設投資效益和社會效益，要求對項目全過程的工程造價進行合理和科學的控制與管理[1]。根據國內外大量的工程實踐，建設項目前期的工程造價控制對項目的成敗起著關鍵作用。如果能夠在項目的前期對工程項目的建設造價和投資進行準確合理的估算，那么項目管理單位對項目造價和投資控制的主動性就越大，項目的風險控制就越有效[2]。

為了實現建設項目造價的快速準確估算，國內外學者提出了多種造價模型或方法，包括第一代的按單位面積的造價估算方法、第二代回歸分析方法及第三代基于現代計算機技術的造價估算模型[2-4]。其中，第三代模型中，人工神經網絡(artificial neural network，ANN)是對數據信息進行處理以及非線性擬合的一種計算方法。通過人工神經網絡構建出的函數，可以揭示所求造價與多個變量間的非線性關系，是一項應用較為廣泛的模型[5]。人工神經網絡可以視為人造大腦，與人腦的神經系統具有類似結構，可提供解決問題的方法。人工神經網絡是通過模擬人腦神經元的信息處理方式，構造大量人造神經元，使其相互聯系在一起的網絡。目前，國內外已有較多學者將人工神經網絡應用建筑工程造價估算領域，且取得了較好的成果[6-16]。人工神經網絡模型目前在自來水廠建設項目造價估算的研究和應用缺乏，這與自來水廠建設內容的復雜性有一定的關系。因此，本研究采用我國西南地區自來水廠建設項目的多組工程造價數據，選取人工神經網絡中的BP算法和RBF算法，進行自來水廠造價模型的構建與優化，并討論不同算法下模型的適用性，以期為類似工程項目的造價估算提供幫助。

1 人工神經網絡模型的構建

模型的功能是結合各種數學手段或計算軟件，確定模型目標值與各類影響因素之間的關系[10]。建立造價模型的第一步，是確定對模型結果有重要影響的相關因素。在人工神經網絡模型中，將模型目標值定義為輸出值，將影響輸出值的相關因素定義為輸入變量[11-16]。本研究選用的數據為收集到的以西南地區為主的18份自來水廠建設項目概預算造價數據，對樣本數據進行分析后，篩選出18個對工程造價的影響因素作為神經網絡的輸入變量，如表1所示。輸出變量確定為2種，分別是自來水廠工程造價(Y1，萬元)及自來水廠噸水造價[Y2，元·(萬m3·d)-1]。

在表1中，編號1～3的變量可以描述自來水廠的基本信息。例如，設計處理規模是自來水廠建設的決定性因素；編號4的價格指數這一變量是用于減小不同年份通貨膨脹帶來的影響，本研究選取國家統計局發布的“建材類工業生產者購進價格指數”，以2018年為基準年，對不同自來水廠的工程造價費用進行調整，盡可能減小通貨膨脹帶來的影響；編號5～18的變量主要為自來水廠的各類生產性和非生產性構筑物，可以針對具有不同工藝路線的自來水廠自由選擇其構筑物種類，選用其建設容積或面積作為變量量化后的數據，即自來水廠選用了6號凈水構筑物，則對該變量輸入體積值，而沒有被選用的7號構筑物則將該變量的體積值輸入為0。

表1 神經網絡輸入變量Tab.1 Input Variables of Neural Network

本研究選用MATLAB軟件中的神經網絡工具箱進行BP和RBF神經網絡模型的構建。首先，將所得的樣本數據按3.5∶1的比例隨機分為訓練組與測試組，即訓練組樣本共14個，測試組樣本4個。

1.1 基于BP算法的模型構建

BP(back propagation)神經網絡是一種前饋神經網絡，網絡由輸入層、輸出層，以及1個或多個隱藏層組成，核心的BP算法依靠誤差逆向傳播的方式，以自學習的方式建立并優化模型。BP人工神經網絡的每一層均由任意個神經元組成，并通過加權連接的方式相互連接。通常可將模型需要預測的值設定為期望輸出值，而與這個預測結果相關的因素定義為輸入層的各個神經元，BP人工神經網絡則是利用算法的不停迭代，擬合出預測結果與相關因素間的最佳關系[8]。

1.1.1 BP神經網絡創建及初始化

調用MATLAB軟件中的newff函數，即可創建出1個BP神經網絡，同時系統將自行對網絡各層的權值和閾值進行初始化。由表1可知，輸入變量為18個，輸出變量為2個，即神經網絡的輸入層共18個神經元，輸出層共2個神經元。同時，還需對BP神經網絡的隱含層層數、各層神經元數量、各層神經網絡激活函數進行設置。本研究根據測試組樣本結果，不斷對網絡結構(即隱含層層數、神經元數量、激活函數)進行調整，以獲取更高準確度的模型。

1.1.2 BP神經網絡訓練和仿真

在完成對BP神經網絡的創建后，導入選定14組樣本數據的輸入變量及輸出變量，利用樣本數據對BP人工神經網絡進行學習訓練。針對不同的神經網絡模型，訓練時需對網絡參數進行適當的設置或調整。表2是神經網絡主要訓練參數及取值。

表2 BP神經網絡主要訓練參數及取值Tab.2 Main Training Parameters and Values of BP Neural Network

對于不同的實際問題，BP神經網絡可選擇不同的訓練函數，本研究選取了常用的Levenberg-Marquardt(trainlm)訓練函數。

1.1.3 確定BP神經網絡的網絡結構

向BP神經網絡中導入表2中的14組訓練樣本數據，通過對樣本數據的學習與訓練，采用默認神經網絡結構的參數，獲得初步的BP神經網絡模型。

然后，使用測試組中的4個樣本數據，對比模型預測值與實際工程造價值的誤差，對模型輸出值的精確度進行校驗。通過不斷調整BP神經網絡的結構，即隱含層層數、神經元數量、激活函數這3項參數，直至模型輸出值與實際工程造價的誤差滿足預期。

本研究中，神經網絡確定了2個輸出值：自來水廠工程造價(Y1)和自來水廠噸水造價(Y2)。因此，本研究對2項輸出值，分別構建具有不同網絡結構的BP神經網絡模型，所得神經網絡模型的網絡結構如表3所示。

表3 BP神經網絡模型結構Tab.3 Structure of BP Neural Network Model

通過MATLAB軟件，構建自來水廠工程造價的BP神經網絡模型，擬合曲線如圖1、圖2所示。其中，虛線代表14組樣本的實際工程工程造價(Y1)或自來水廠噸水造價(Y2)，實線代表基于BP神經網絡模型對14組樣本的預測值。由圖1、圖2可知，2條曲線的重合程度非常高，即代表BP神經模型對樣本數據的擬合程度很好。

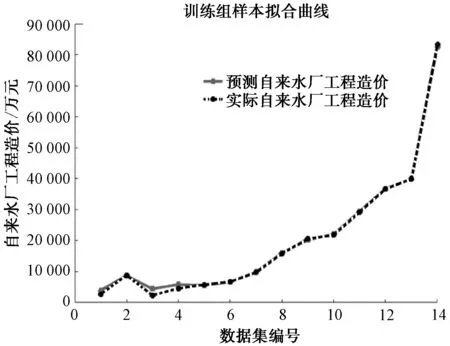
圖1 工程造價(Y1)的BP模型擬合情況Fig.1 Fitting Situation of BP Model for Construction Costs (Y1)

圖2 噸水工程造價(Y2)的BP模型擬合情況Fig.2 Fitting Situation of BP Model for Unit Construction Cost (Y2)

1.2 基于RBF算法的模型構建

RBF(radial base function)神經網絡是一種局部神經網絡，具有結構簡單、訓練簡潔、學習收斂速度快等優點[6]。與BP神經網絡一樣，能夠以任一精確度逼近連續函數。與BP神經網絡相似的是，RBF神經網絡同樣也由3部分組成：第1層是輸入層，神經元數量由輸入變量的個數決定；第2層是隱含層，網絡的激活函數選用的是徑向基函數；第3層為輸出層，采用線性激活函數。

調用MATLAB軟件中的newrb函數，即可創建出1個RBF神經網絡。向RBF神經網絡中導入14組訓練樣本數據，網絡將自動對樣本數據進行反復的學習與訓練，自行確定RBF神經網絡的結構，無需進行如BP神經網絡的參數調整工作，只有1個參數spread需要調整，取默認值1.0。RBF的網絡結構如表4所示。

表4 RBF神經網絡模型結構Tab.4 Structure of RBF Neural Network Model

通過MATLAB軟件構建出的自來水廠工程造價的RBF神經網絡模型，擬合曲線如圖3、圖4所示。其中，虛線代表14組樣本的實際工程造價(Y1)或自來水廠噸水造價(Y2)，實線代表基于RBF神經網絡模型對14組樣本的預測工程造價值，2條曲線的重合程度越高，則代表RBF神經模型對樣本數據的擬合程度越好。由圖3、圖4可知，虛線和實線的重合程度極高，二者幾乎完全重合，即代表RBF神經模型對樣本數據擬合程度高。

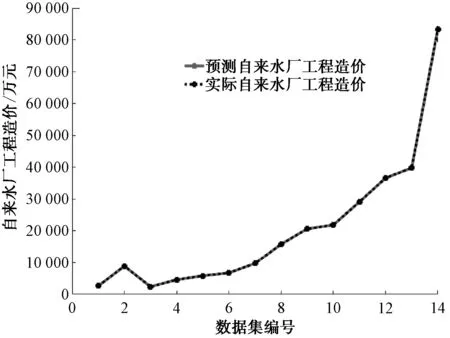
圖3 工程造價(Y1)的RBF模型擬合情況Fig.3 Fitting Situation of RBF Model for Construction Costs (Y1)

圖4 噸水工程造價(Y2)的RBF模型擬合情況Fig.4 Fitting Situation of RBF Model for Unit Construction Cost (Y2)

2 BP與RBF神經網絡模型的校驗與對比評價

2.1 BP與RBF神經網絡模型的實例校驗

使用MATLAB軟件構建的基于BP和RBF的造價模型，是建立于14組訓練樣本之上的一類特殊“經驗”模型，而非理論推導模型，因此，需通過實際案例數據的檢驗，以判斷人工神經網絡模型的準確性。

本研究中使用訓練樣本以外的4組樣本作為測試數據，代入神經網絡模型中，可得到自來水廠工程造價(Y1)和自來水廠噸水造價(Y2)2項輸出值的預測結果，結合工程的實際值可計算模型的預測誤差。校驗結果如圖5、圖6所示。

圖5 水廠項目工程造價(Y1)的模型校驗結果Fig.5 Verification Results of ANN Model (Y1)

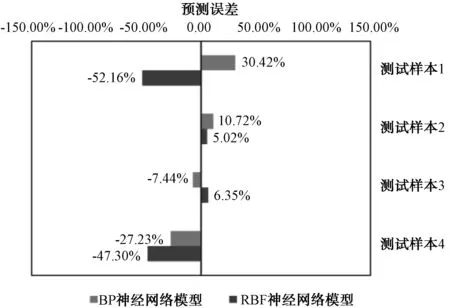
圖6 噸水工程造價(Y2)的模型校驗結果Fig.6 Verification Results of ANN Model (Y2)

由圖5、圖6可知，對于2項指標Y1和Y2，BP神經網絡模型的測試樣本預測誤差均可控制在±30%或更低，且5/8的測試樣本可將誤差控制在±20%，預測效果在項目早期階段，認為是可以接受的；而對于RBF網絡模型，僅有3/8的測試樣本誤差小于±15%，且5/8的測試樣本誤差接近或超過±50%，誤差過大，通常無法接受。

2.2 BP與RBF神經網絡模型的對比評價

由圖1～圖4的模型擬合結果可知，RBF神經網絡模型對于訓練樣本數據的泛化能力要強于BP神經網絡模型，模型預測曲線幾乎完全貼近樣本數據的實際值。但由圖5和圖6的對比結果可知，對于自來水廠工程造價(Y1)和自來水廠噸水工程造價(Y2)2項輸出值，BP神經網絡模型的估算精度遠遠優于RBF神經網絡模型，且預測穩定性更高。與RBF神經網絡僅具有1個可調參數相比，BP神經網絡的構建過程需要定義多種類型的參數和確定神經網絡的結構等，構建過程相對更加困難。

本研究中得到的預測精度結果與劉婧等[6]的模型驗證結果相反，對于RBF神經網絡模型的預測誤差遠大于BP網絡模型的結果，可能原因如下。

(1)樣本數據量較少。RBF網絡模型對樣本泛化能力過強，反而易受到樣本中極端值的影響，導致模型誤差率變高。

(2)BP神經網絡模型在構建過程中，除模型本身的學習訓練外，還經過了多次網絡結構的手動調整，以提高其準確度。因此，BP神經網絡模型相對更穩定且精確度更高。

3 結論

本研究采用人工神經網絡技術構建了基于BP算法和RBF算法的自來水廠工程造價模型。針對水廠建設項目的造價特性，篩選出18個相關影響因素作為輸入變量，通過對已有訓練樣本的學習，構建神經網絡模型。其中，基于BP算法的人工神經網絡模型具有較好的預測能力，87.5%測試樣本的校驗結果表明，均可達到項目建議書階段的估算精度要求(±30%)，50%以上的樣本可以達到可行性研究報告的估算精度要求(±20%)。隨著累計案例數目的增加，該模型或算法的精確度會不斷提高。基于RBF算法的人工神經網絡模型估算精度較差，僅有3/8的樣本可以達到項目建議書階段的估算精度要求(±30%)，無法滿足實際的工程需求。