高階振型對超高層建筑基底剪力的影響

李陽陽，陳成欣，閆康行

（宿州學院，安徽宿州234000）

0 引言

改革開放以來，得益于建筑材料的不斷改進、設計理論的不斷完善以及施工工藝的不斷發展，近幾十年以來我國已建成的超高層建筑有幾千棟，尤其是各地地標性超高層建筑的迅速發展，例如1983年竣工的南京金陵飯店（110m）、1990年竣工的香港中銀大廈（367.4m）、2010年竣工的香港環球貿易廣場（484m）、2015年竣工的天津117大廈（596.5m）［1］。隨著建筑高度的增加，結構變得越來越柔，自振周期變大而自振頻率隨之降低，在風荷載的作用下當出現結構二階及以上高階振型的自振頻率位于其功率譜的主要頻帶寬度范圍內時，高階振型對結構基底剪力的影響便不可忽略［2-5］。

對于頻譜比較稀疏的結構，我國《建筑結構荷載規范》（以下簡稱荷載規范）采用風振系數法確定結構的風荷載及其基底剪力，計算風振系數時僅考慮第一階振型的貢獻［6］。相應地，對于自振周期比較稀疏的結構，第一階振型一般對結構的風振響應起控制作用，荷載規范的風振系數法比較簡單實用，且準確度高。然而，對于近年來快速發展的地標性超高層建筑，由于結構前幾階振型的自振頻率較低，僅考慮第一階振型評估超高層建筑的基底剪力時，就可能會出現偏于危險的結果［7-9］。鄒垚通過大量算例分析了高階振型對矩形截面高層建筑橫風向風振響應的貢獻，指出二階振型對加速度的影響不容忽視，在計算建筑結構的風振加速度時應該考慮二階振型的貢獻［10］。

在X和Y方向，本文以某一具有“靴子狀”外形的超高層建筑為工程背景，基于隨機振動理論分別采用平方和開平方根方法（square root of the sum of the squares，簡稱SRSS）和完全二次項組合方法（complete quadratic combination，簡稱CQC）計算結構基底剪力，并與只考慮第一階振型的計算方法（Fundamental Mode Method，簡稱FM方法）得到的結果進行對比分析，研究高階振型對超高層建筑結構基底剪力的影響，以此來校驗荷載規范計算方法的準確性和可靠性。

1 計算推導

1.1 基本假設

受來流紊流、氣動反饋和尾流脫落等因素的影響，風對結構的作用機理十分復雜。氣流具有慣性和粘性的特點，當其流經建筑結構時會產生旋渦形成、尾流脫落等現象，形成復雜的流固耦合相互作用，從而引起結構振動。因此，準確定量地分析風對結構產生的作用基本是一種理想的情形。本文風荷載引起結構基底剪力的計算基于如下假設［11］：

（1）平均風速vˉ()z符合指數分布

式中，α為地面粗糙度指數分別為結構高度z處、建筑頂部高度H處的平均風速。

（2）準定常假設

結構表面t時刻位置Mi( )x,y,z的脈動風壓w(Mi,t)為：

（3）單位高度的質量m0假定沿高度不變。

（4）迎風面和背風面產生的壓力完全相關，變化同步。

1.2 計算公式

大氣邊界層中的風由遠離建筑物自振周期的平均風和接近于建筑物的脈動風兩部分組成，前者對結構產生的作用是靜力性質的，后者對結構產生的作用是動力性質的。平均風的周期一般在10分鐘以上，對結構產生的荷載稱為平均風荷載；脈動風具有紊流特性，是由于風的不規則性引起的，對結構產生的脈動風荷載與結構自振頻率、節點質量有一定的關系，需要運用隨機振動的理論知識進行分析［12］。下面分別對平均風荷載、脈動風荷載和基底剪力的計算公式進行推導說明。

1.2.1 平均風荷載

結構z高度處的平均風荷載pˉ()z，計算公式如下：

式中，影響函數i(z,zi)為：

1.2.2 脈動風荷載

由振型分解反應譜法可知，結構第j振型的運動方程為：

式中，ξj(t)為第j振型的廣義坐標分別為建筑物第j振型的質量、瑞雷阻尼、剛度和風荷載，φj()z為結構z高度處第j振型坐標。依據隨機振動理論，結構z高度處的位移響應功率譜密度Sy(z,n)為

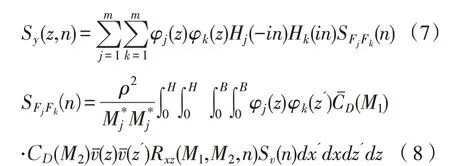
式中，nj結構振型的自振頻率，SFjFk(n)為第j振型與第k振型的廣義力互譜密度，H為結構迎風面寬度為結構M1、M2兩點的準定常壓力系數，均等于風荷載體型系數，Rxz(M1,M2,n)為脈動風速互相干函數的平方根，Sv(n)為脈動風速譜。Hj(-in)和Hk(in)為傳遞函數，表達式如下：

根據風致位移響應和廣義力互譜密度之間的關系，響應y的方差σ2y為

式中，σyj(z)為結構第j振型的位移響應根方差，Sy(z,n)為位移的互譜密度函數，σyjk(z)為第j振型、第k振型交叉位移響應根方差。式（7）為準確計算結構脈動風荷載的CQC方法，當忽略第j振型、第k振型的交叉項時，表達式簡化如下：

此時公式（8）演變為SRSS方法，式中σyjb(z)、σyrb(z)分別為背景響應、共振響應的根方差。

由位移響應根方差可得，第k振型對應j振型下的脈動風荷載為

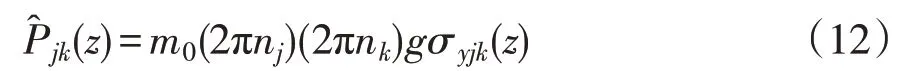
式中，g為峰值因子，本文取2.5。

1.2.3 等效靜力風荷載

結構各樓層的等效靜力風荷載，計算公式如下：

式中，Wjk為振型參與系數，表達式為：

1.2.4 結構基底剪力

2 算例分析

以某一具有“靴子狀”外形的超高層建筑為工程背景，結合剛性模型表面測壓風洞試驗，分別采用考慮高階振型的SRSS方法、CQC方法，以及僅考慮第一階振型的FM方法計算超高層建筑結構的基底剪力，并對比分析三種方法得到的計算結果，研究高階振型對超高層建筑基底剪力的影響，以此來校驗荷載規范計算方法的準確性和可靠性。風向角如圖1所示。

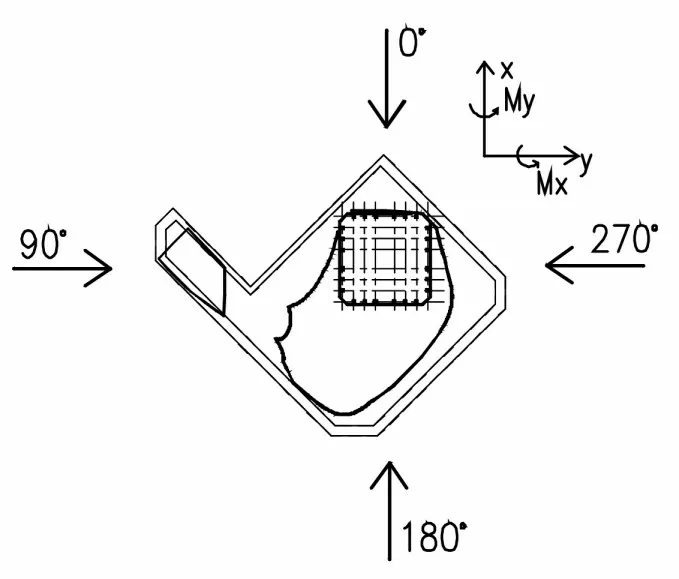
圖1 風向角及坐標示意圖

2.1 結構動力特性

建筑結構阻尼比選取為0.04，模型比例與實際建筑的比例為1:300，結構的前9階振型的自振頻率及廣義質量經計算分析，如表1所示。

表1 結構各振型的廣義質量及自振頻率

2.2 結構基底剪力

依據基本風壓、結構阻尼比、自振頻率、廣義質量等數據，在結構X、Y方向分別采用SRSS方法、CQC方法計算得到了考慮前三階振型的結構基底剪力VSRSS、VCQC，以及僅考慮第一階振型FM方法計算得出的結構基底剪力VFM，VSRSS為SRSS方法計算得出的結構近似基底剪力，VCQC為CQC方法計算得出的結構準確基底剪力。FM方法、SRSS方法得出的結構基底剪力誤差定義如下：

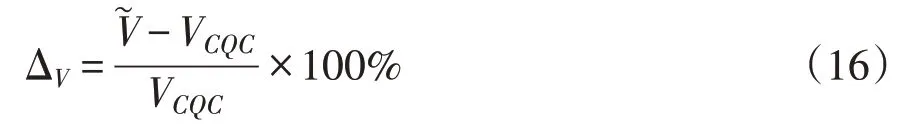
式中，V?為FM方法、SRSS方法計算的結構近似基底剪力。基底剪力誤差值ΔV的絕對值越大說明誤差越大，ΔV小于0說明結果偏小，ΔV大于0則說明結果偏大。圖2給出了0～350°在X和Y方向結構基底剪力沿風向角的誤差變化情況。

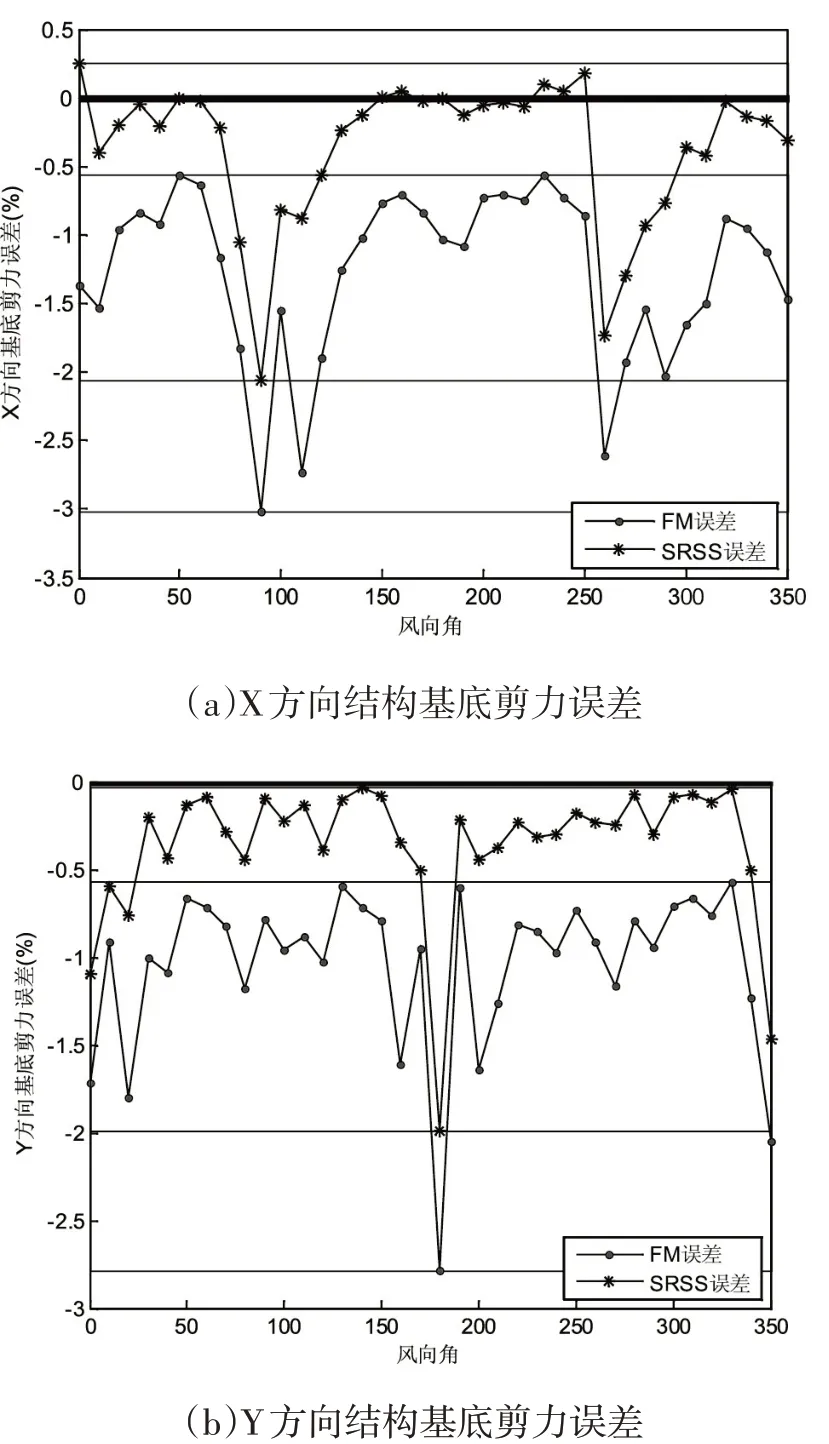
圖2 X和Y方向基底剪力誤差沿風向角的變化圖

對于FM方法、SRSS方法計算得到結構基底剪力，從圖2中可以得出如下結論。

（1）在X方向，FM方法的最大誤差發生在50°，為-0.52%，最小誤差發生在90°，為-3.13%；SRSS方法的最大誤差發生在0°，為0.27%，最小誤差發生在90°，為-2.11%。在Y方向，FM方法的最大誤差發生在330°，為-0.54%，最小誤差發生在180°，為-2.79%；SRSS方法的最大誤差發生在140°，為-0.04%，最小誤差發生在180°，為-1.96%。

綜上可得，在X和Y方向，FM方法計算得出的結構基底剪力誤差均在5%以內，滿足工程精度要求。高階振型及振型之間的交叉項對于超高層建筑結構基底剪力的影響較小可以忽略不計，對于基底剪力起控制作用的是第一階振型，計算結構基底剪力時，可采用荷載規范中僅考慮第一振型的風振系數法。

（2）FM、SRSS方法計算的結構基底剪力誤差沿風向角的變化趨勢基本一致。在X方向，FM方法最小誤差均發生在90°；在Y方向，FM方法最小誤差均發生在180°。

（3）FM方法和SRSS方法計算得到的結構近似基底剪力，相比順風向，橫風向的誤差出現了較大的誤差。在X方向，90°和270°附近（橫風向）的結構基底剪力誤差較大；在Y方向，0°和180°附近（橫風向）的結構基底剪力誤差較大。

3 結論

（1）高階振型及振型之間的交叉項對于超高層建筑結構基底剪力的影響較小可以忽略不計，計算結構基底剪力時，可采用荷載規范中僅考慮第一振型的風振系數法。

（2）FM方法、SRSS方法計算的結構基底剪力，兩者誤差沿風向角的變化趨勢基本一致。

（3）FM方法和SRSS方法計算得到的結構近似基底剪力，相比順風向，橫風向出現了較大的誤差。