中小學圓形知識分布的研究現狀及研究意義

馬小麗

摘 要：幾何課程與教學改革一直是數學教育研究的熱點，其在培養學生三維空間能力、形象思維能力、合情推理、解析幾何觀念的樹立等方面發揮著重要作用。圓形是貫穿義務教育階段和高中階段的幾何課程內容中的重點內容之一，歷來有很多研究者對其進行了多角度、多層面、多維度的研究和論述，但總體來看，在現有的聚焦平面幾何中圓形知識的研究成果中，大多是從幾何學的整體角度出發對整個平面幾何開展的研究，鮮少出現具體的、有針對性地、專門性地對中小學圓形知識展開詳盡的、系統的、專門的研究。

本文重在介紹幾何課程在國內外研究的歷史和現狀，在詳實闡述和歸類關于幾何研究的文獻綜述的基礎上，提出了本文擬研究的問題，闡明了研究的目的與意義，介紹了研究的方法與框架。

關鍵詞：義務教育階段;平面幾何;中小學;圓形;呈現方式

中小學圓形知識分布的研究現狀及研究意義

數學中以空間形式（簡稱形）為研究對象的分支，叫做幾何學。

斯托利亞爾曾指出：“幾何教學問題是中等數學教育現代化的最復雜的問題之一，它引起了廣泛的、世界性的爭論”[1]。作為理性思維培養最好的載體的幾何課程，成為國際上歷次數學課程改革的焦點。

圓形是貫穿中小學平面幾何課程的重要內容，圓形是一種基本的幾何圖形，圓形是在環繞中心旋轉時唯一一種自己能沿著自己滑行的曲線，而且，圓形物體在生活中時時、處處存在。

筆者在閱覽國內外大量文獻資料的基礎上，對有關幾何課程和圓知識的相關研究和有關文獻資料整理歸納如下：

（一）關于幾何思維水平分析的理論

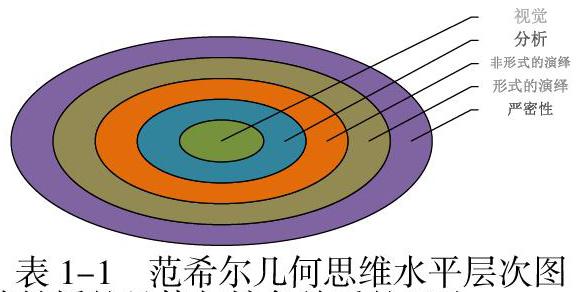
1.范希爾理論

對充足的一線教學經驗進行理論層面的概括和提升的范希爾理論，被國外許多國家引為數學課程編寫的依據來設計幾何課程，該理論的主要觀點是：幾何思維水平有五個層次[2]，如圖所示：

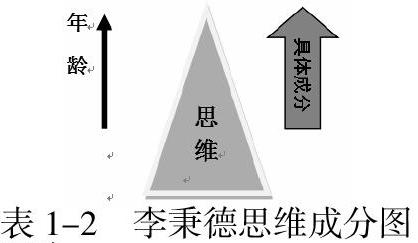
2.李秉德教授的具體與抽象關系的理論

該理論指出：人類隨著年齡的增長，思維中的具體成分和抽象成分是此消彼長的關系。在中小學生求學階段，尤其是小學學習階段，由于小學生心智水平的不成熟和不穩定性等因素的局限，小學生思維的主體就是具體成分;但到了中學階段乃至以后，中學生和高中生的思維中盡管思維中的抽象特質已經具備，但其思維中的具體成分依然大量存在[3]。如圖所示：

3. SOLO分類理論

在皮亞杰的發展階段論的基礎上，彼格斯（John B. Biggs）教授經過長期的研究和探索，形成了評測某人回答問題時所展現的思維結構的SOLO分類評價理論，即 “可觀察的學習成果結構”（structure of the observed learning outcome），英文縮寫為SOLO，意為：觀察到的學習成果的結構。

（二）關于幾何教學的教學研究及實踐調查研究

1.教學研究方面

這方面的學術成果有：劉春曉的在評述義務教育階段幾何課程改革的基礎上，重點分析了數學史指導下的幾何教學的途徑及在幾何教學中運用數學史的具體方案;王靜和張和平則分別在闡明幾何教學生活化和幾何直觀性水平的內涵和特點的基礎上，總結出初中幾何教學生活化的有效策略和幾何直觀性教學原則，對一線教育者有效開展幾何教學提供了指導。不僅如此，有學者還從幾何教學的工具開發和技術支撐方面的問題進行了探索，如江錫晨的《小學幾何教學支撐工具的設計和開發》和劉君紅的關于“幾何畫板”在高中數學課堂中的引入的文章，探討了如何在教學中生動形象地呈現幾何圖形的問題;再則，聚焦幾何教學中某一領域的問題，如幾何解題和幾何符號教學等方面，有代表性的文章有：張杰的《關于中學數學幾何機械化解題的教學研究》和徐媛的《義務教育階段數學符號教學的研究》。

2.實踐調查研究方面

調查研究應能采集有代表性的樣本和較強的操作性，得出的結論令人信服。華東師范大學于曉暉在甄別空間能力、空間想象力等概念的基礎上，開展調查研究，經過數據整理與分析，考慮了空間觀念的六個方面對學生空間觀念的發展影響，發現大部分學生能夠形成表象并能在頭腦中對表象進行操作，進而給教師的幾何實際教學提出了一些建議。

（三）課標解讀及課標視角下對幾何教學某一角度的研究

現今時代日新月異的信息技術是教育的現代化在教育領域的卓越表現，而這也在一定程度上促進了數學課程改革的步伐。文化是社會進步的先導，課標是教育的先導，在這方面，國外的很多國家，尤其是美國，走在了教育改革的最前方。日本也不甘落后，努力使自己在課程編排和指導思想上與時俱進。世界各國紛紛推出了數學課程標準來適應新時代的數學教育需求。

在我國，課標改革也在如火如荼地進行著。2001年，教育部頒布了《基礎教育課程改革綱要（試行）》。2011年經教育部批準，《義務教育數學課程標準（2011年版）》在全國范圍內實行。

相應的，在學術領域，出現很多解讀新課標的著述和文章。孔凡哲等人立足國內外中小學數學課程標準及各種版本的數學教材的對比分析，并結合新課標的深入剖析，認為：義務教育階段幾何教學旨在使學生在空間觀念、合情推理和演繹論證等方面獲得發展。

與此同時，涌現出了許多從新課標的視角對數學中“空間與圖形”的研究和教學方式的實踐研究的文章，系統分析了新課標中幾何教學的理念和要求，對教師幾何語言的運用、幾何教學內容的整合、教學方法的策略等方面都提供了可行性的建議。

（四）不同版本數學教材中幾何內容的比較研究

在課標的指導下，各地結合自身的教學實際和教學資源，開拓了不同版本的數學教材：人教版、北師大版、蘇教版、湘教版等，這些版本的數學教材在幾何知識呈現方式、課程的編寫體例、課程難易程度和教學順序的設置等方面都有所不同。很多學者和教師亦對以上不同版本的數學教材中的幾何內容從不同角度給予研究，如學者周遠方對比分析了四套高中數學教材的結構方式，經過客觀對比分析后，針砭指出各個版本的數學教材的長處和不足，為高中數學教材的編排出謀獻策。

（五）以“圓”作為分析載體的研究

總體來看，國內外的文獻資料中對平面幾何中的“圓”進行專題研究的著述并不多，但以圓形作為研究分析的載體的范例卻時有出現，如有用“圓”章節體現數學史運用途徑的研究;有以“圓”概念的教學引出概念圖教學應用性研究等。

（六）與圓知識有關的教學案例及教學實錄

在有關“圓”知識的文獻資料中，最多的莫過于與圓形知識有關的教學案例和教學實錄方面的資料。這些資料大都通過真實的課堂教學活動設計，展現教學互動，體現知識生成過程，從而彰顯教師的教學風格，并有注重幾何知識源于生活，密切聯系生活的特征。

綜觀中小學數學教材中的幾何知識，圓形是每個學段都需學習的重要的幾何課程內容，是幾何部分中重中之重的內容，但在現有研究中，并未涉及到對圓形知識展開系統深入的探討，更沒有對在學段時間方面和學生認知結構方面都具有較強銜接性和連貫性的中小學階段圓形知識的分布情況和分布特征等方面的系統分析。

畢達格拉斯說：“一切平面圖形中最美的是圓”[4]。圓是一種基本的、和諧的、美麗的、具有同一形狀的特殊的幾何圖形。其作為幾何圖形之一，有獨特的區別與其他幾何圖形的特性。同時，圓知識也是貫穿義務教育和高中教育的幾何課程內容，在平面幾何占有舉足輕重的地位。

回顧之前數學學者及教育從業者的研究，基本上是從總體上對平面幾何知識進行探討與研究，并沒有學者對具體的圓形知識進行系統的研究，本文擬通過對圓形知識的系統研究和分析，希望通過對圓形知識在不同學段的知識特征的研究，結合學生的幾何思維水平，進一步分析學生該怎樣更好地學習圓形知識，老師應如何高效地教授圓形知識，進而將研究成果和結論拓展和應用到一般的平面幾何課程內容的實際教學過程中。