培養山區農村初中生幾何解題能力的教學嘗試

覃鎬生

摘?要：教師在教學中培養山區農村初中學生幾何解題能力，幫助學生建立完整的解題體系。解題步驟：第一步，教育學生學會審題。第二步，教育學生重新畫圖。第三步，教育學生在重新畫的圖形上標出已知的數據。第四步，教育學生采用適當的方法解決幾何問題。1. 教育學生用順推證法解題。2.教育學生用逆推法解題。3.教育學生用兩邊齊頭并進法解題。通過多次反復訓練和培養，就一定能養成良好的幾何解題能力的習慣。

關鍵詞：培養?幾何解題能力?教學嘗試

新課程標準的課程總目標中提出：“通過義務教育階段的數學學習，學生能獲得適應社會生活和進一步發展所必需的數學的基礎知識、基本技能、基本思想、基本活動經驗。”一線數學教師在幾何課堂教學時是否落實這個目標，成為評價一節課成功與否的標準之一。這里的基本技能在平面幾何教學中包括解題技能。培養山區農村初中學生幾何解題能力，幫助學生建立完整的解題體系，成為每個教師都必須努力的方向。

目前，本人工作的地方處于山區農村地區，山區農村初中學生普遍存在這些情況：面對幾何題目不愛動手，不愛動口，不會思考，給教師的教學工作造成了很大障礙。本人從培養山區農村初中生幾何解題能力的教學嘗試和大家探討。

第一步，教育學生學會審題。相信很多山區農村教師都會遇到這樣的問題：山區農村初中生理解能力和閱讀能力非常低下，學生讀題花了很多時間，造成課堂教學效率不高。造成這種情況的原因是學生不會審題。審題即是根據題目，弄清哪些是已知條件和題目所要求證的是什么。審題是正確理解題目的前提。審題是閱讀能力和理解能力的綜合。在課堂教學時，教師可以通過讓學生集體讀題或者個別學生讀題，再由學生討論題目，討論的內容包括已知的是什么，從已知條件可以得到哪些結論，題目涉及哪些知識點，最后得到解答題目的方法。

第二步，教育學生重新畫圖。教師要求學生在草稿紙上把題目中的圖形重新畫出來，這個過程中教師要求學生要把圖形畫得越標準越好。它的主要作用是通過學生動手操作畫圖，把題目中的已知條件經過大腦再次呈現出來，有利于學生綜合運用已知條件解答題目。

第三步，教育學生在重新畫的圖形上標出已知的數據。把數據既形象又直觀地展示出來。這里分兩種情況：

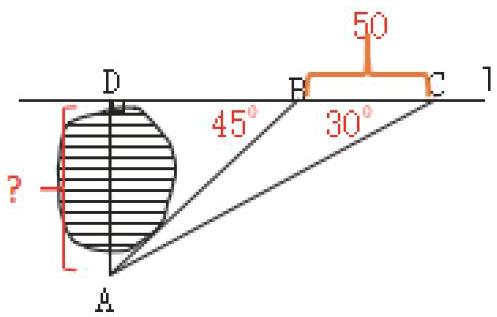
①當已知條件中的量不相等時，在畫出來的圖形中把已知數據標出來。如圖，小明家在A處，門前有一口池塘，隔著池塘有一條公路l，AB是A到l的小路。 現新修一條路AC到公路l.小明測量出∠ACD=30?，∠ABD=45?，BC=50m。請你幫小明計算他家到公路l的距離AD的長度。

圖形標上數據后，對于學困生來說就很容易看出來哪些是已知的與哪些是需要求解的，還可以推導∠DAB=45與∠DAC=60，從而得到AD=BD。

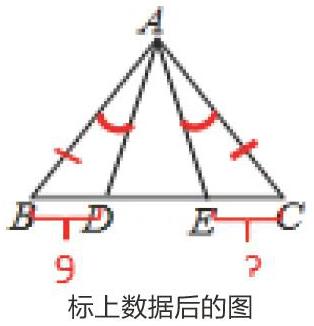
②當已知條件中有相等的量時，用相同的符號把表示相等的量標出來。如2019年四川省成都市中考數學試卷第12題，如圖，在△ABC中，AB=AC，點D，E都在邊BC上，∠BAD=∠CAE，若BD=9，則CE的長為_____。

圖形標上數據后，對于學生來說就很容易看出來AB和AC是相等的，∠BAD和∠CAE是相等的，通過推導得到∠B=∠C，從而得到△ABD與△ACE全等，得出BD=CE=9。

第四步，教育學生采用適當的方法解決幾何問題。波利亞曾說過：“解題的成功要靠正確思路的選擇，要靠從可以接近它的方向去攻擊堡壘。為了辨別哪一條思路正確，哪一個方向可接近它，就要試探各種方向和思路。”解決數學問題的方法多種多樣，對于山區農村初中學生來說能解決問題的方法就是最好的。

1.教育學生用順推證法解題。對于初中階段的很多幾何題目，都可以用順推證法解決問題。一般，利用題目中的已知條件（包括隱藏著的條件）或者是某些數學定義、公理、定理等，經過一系列的推理論證，最后推導出所要證明的結論成立，這種證明方法叫作綜合法。綜合法又叫“順推證法”或“由因導果法”。如圖，矩形ABCD中，AB>AD，把矩形沿對角線AC所在直線折疊，使點B落在點E處，AE交CD于點F，連接DE。（1）求證：△ADE≌△CED。

分析：要想證明△ADE≌△CED，結合題目給出的條件，由于四邊形ABCD是矩形，所以得到AB等于CD，BC等于AD，再由折疊的性質可以得到AB等于AE，BC等于CE，綜合上面兩個結論得到AE等于CD，AD等于CE，得到兩條邊相等的情況下，根據全等三角形的判定條件，再找一條邊或這兩條邊的夾角相等就可以證明這兩個三角形全等。從題目的圖形不難找到DE是公共邊這一條件，證明的過程是遵循著分析的過程寫出來的，從而解決了問題。

2.教育學生用逆推法解題。逆向思維是一種從問題的相反方向思考的思維方式。這種運用逆向思維的方式來解決問題的方法就是逆推法。逆推法是一種更容易體現學生思考和解決問題過程的方法。逆推法解決問題的目的性更強，對于山區農村初中生思考問題和解決問題的思路更清晰，書寫解題的步驟更有條理。例題再現：如圖，⊙O是△ABC的外接圓，AC是直徑，過點O作OD⊥AB于點D，延長DO交⊙O于點P，過點P作PE⊥AC于點E，作射線DE交BC的延長線于F點，連接PF。（1）若∠POC=60，AC=12，求劣弧PC的長（結果保留π）;（2）求證：OD=OE。

分析：要想證明OD=OE，也就是證明兩條線段相等，可以通過證明兩個三角形全等得到全等三角形的對應邊相等，即證明△AOD≌△POE。那么如何證明△AOD≌△POE呢？從題目的圖形可以得到兩個條件：①因為OA和OP都是圓的半徑，所以OA=OP，②∠POE和∠AOD是對頂角，所以∠POE=∠AOD。再從題目中給出OD⊥AB，PE⊥AC，可以得到第三個條件∠ADO和∠PEO都是直角，即∠ADO=∠PEO=90。那么證明△AOD≌△POE的問題就解決了。證明的過程與分析的過程剛好相反，解決問題的目的性更強。

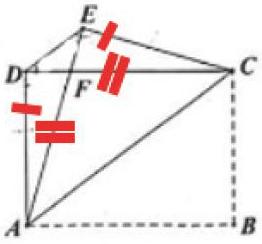
3.教育學生根據題目的已知條件和求證聯想學過的知識點，再把這些結論串聯起來。當遇到一些難度比較大的題目時適合運用這種方法，也就是當看到這道題時，一時間沒有什么頭緒，運用前面的幾種方法都難以解決時，就從已知條件出發，用學過的知識點可以推出哪些結論，再由結論聯想用哪些學過的知識才能推出這個結論，看能否串聯起來。我把它稱為兩邊齊頭并進法。例題再現：如圖，四邊形ABCD是正方形，點E是邊BC的中點，∠AEF=90°，且EF交正方形外角平分線CF于點F。求證：AE=EF。

分析：首先從已知條件出發，四邊形ABCD是正方形，可以得到AB=BC=CD=AD，∠DAB=∠B=∠BCD=∠D，再從點E是邊BC的中點，可以得到BE=EC，從圖形和∠AEF=90°的位置關系可以推導出∠BAE=∠FEC，但依然沒有辦法推導出AE=EF。另一個方面我們從結論出發，要證明兩條線段AE和EF相等，嘗試證明兩個三角形全等，但這里沒有符合條件的兩個三角形，只能通過構造出來。①過F作FG垂直BC，再證△ABE≌△EGF全等，顯然是行不通，因為這兩個三角形中沒有對應邊相等。②取AB的中點G，連接EG，證△AGE≌△ECF。這里可以推導出AG=EC=BG=BE，得到∠BGE=∠GEB=45，推導出∠AGE=135，從EF交正方形外角平分線CF于點F可以得到∠EGF=135，故∠EGF=∠AGE=135。再聯合前面得到的∠BAE=∠FEC，AG=EC，從而得到△AGE≌△ECF，推出AE=EF。我們對于一時無法解決的問題，就要思考從兩邊入手，把推導的結果串聯起來，眼前的問題會迎刃而解。

學生的幾何解題習慣是通過多次反復訓練和培養出來的，只要教師在教學中不斷提醒，堅持不懈地努力奮斗，就一定能提高學生的幾何解題能力，也會提高我們的數學教學的效果和質量。

參考文獻

[1]朱剛.初中數學函數與幾何綜合題解題策略研究[J].中學數學，2019（20）：76-77.

[2]查書平.淺析綜合法和解析法在初中幾何解題中的應用[J].數學學習與研究，2019（15）：142.