“平拋+斜面”模型六大解題策略

福建 饒華東

平拋運動是考查“運動合成與分解”相關知識的重要載體，同時還可以結合功能關系考查，歷來是高考的重點和熱點，高考真題和各省質(zhì)檢試題中結合體育運動、生產(chǎn)勞動、軍事訓練等考查平拋運動的題目層出不窮。這些試題中“平拋+斜面”模型又是最常見的，特別是在2007年至2013年期間幾乎每年都有高考試題涉及該模型(見表1)。2020年第32屆夏季奧運會在日本東京舉辦，2022年第24屆冬季奧運會則將在我國由北京和張家口聯(lián)合舉辦，在此背景下，以跳臺滑雪、飛鏢投擲等體育運動為情景的“平拋+斜面”模型(或其衍生模型)，有可能再次進入命題專家的視野，2020年考生在高考備考時應該重視這一點，本文從六個方面闡述了“平拋+斜面”模型的解題策略以期對考生有所幫助。

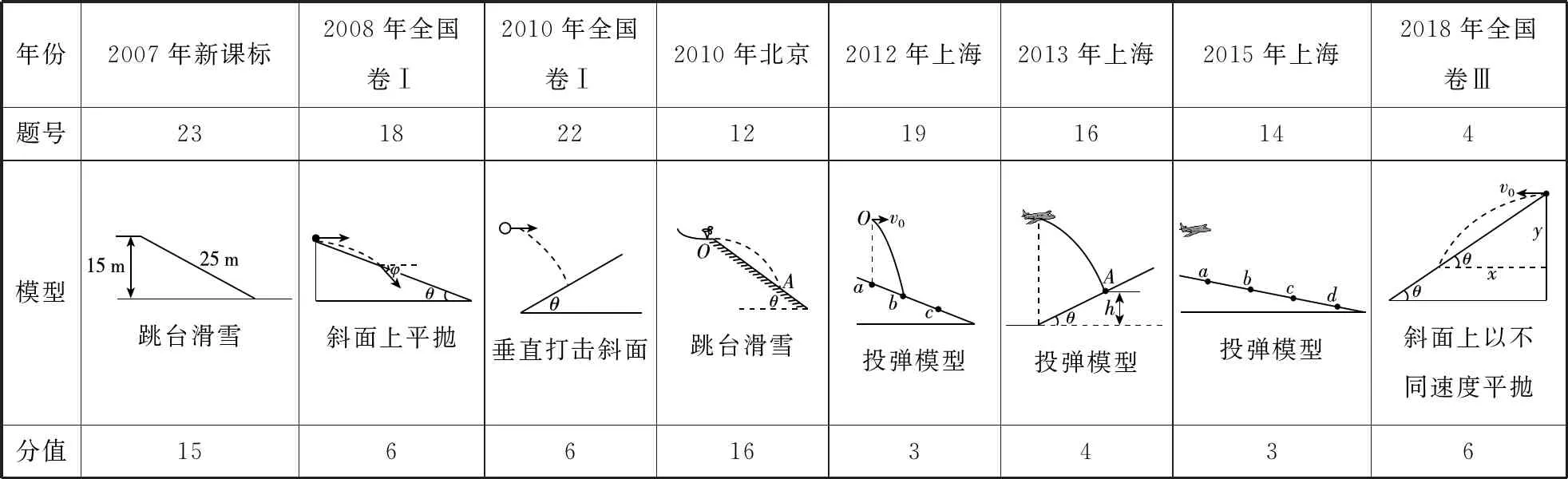
表1 2007～2018年間“平拋+斜面”模型高考題統(tǒng)計

一、化曲為直，變難為易

平拋運動是勻變速曲線運動，運動過程中加速度不變，但速度方向和位移方向時刻在變，直接分析將會感到無從下手，如果將平拋運動分解為水平方向的勻速直線運動和豎直方向的自由落體運動，對運動過程的分析將變得簡單明了。

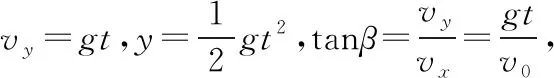
圖1

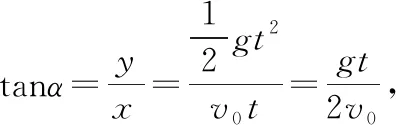
【例1】(2008年全國卷Ⅰ第14題)如圖2所示，一物體自傾角為θ的固定斜面頂端沿水平方向拋出后落在斜面上。物體與斜面接觸時速度與水平方向的夾角φ滿足

( )

A.tanφ=sinθB.tanφ=cosθ

C.tanφ=tanθD.tanφ=2tanθ

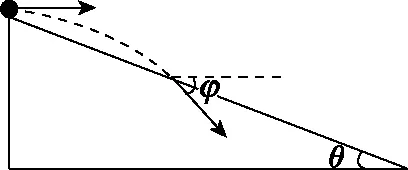
圖2

【解析】φ為速度與水平方向的夾角，而θ等于位移與水平方向的夾角，直接套用前面分析得出的結論：做平拋運動的物體，任意時刻速度與水平方向夾角的正切值是位移與水平方向夾角正切值的兩倍，故選項D正確。……