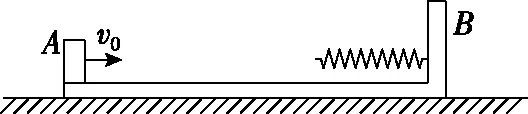
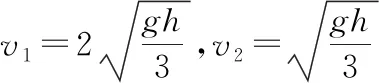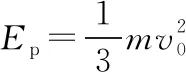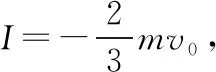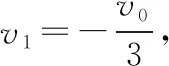一題多變，玩轉滑塊、滑板

河北 聶震萍 康利軍

板塊模型是高中物理的經典模型，它由一個或多個滑塊疊放在木板上，通過某些力使二者發生相互作用，從而使板、塊間發生一系列與相對運動相關的過程，是考查學生靈活運用力學三大規律解決物理問題的常用載體，故備受命題者的青睞。從命題的情景上看，此模型又常通過多滑塊、多過程、或外加擋板、彈簧等輔助器件進行考查，使得構成的物理情景多樣化；從知識的考查上看，此模型既可以考查動力學相關規律，也可以考查動量和能量的綜合運用；從學科素養的養成來看，由于此模型綜合性強，不僅可以加深學生對加速度、動量、能量等多個物理概念的理解，使物理觀念得到提煉和升華，還可以通過多個規律的綜合考查，使學生的模型建構、綜合分析、推理論證等科學思維內化為能力。示由此可見，板塊問題由于涉及研究對象多、運動過程多、知識規律考查多，使得學生在解題方法的選擇上感到混亂，甚至無從下手，故本文將以2019年江蘇卷第15題為例，通過一題多變的方式，對常見的板塊問題予以分析和歸納，希望對同學們解決此類問題有所幫助。

【母題】(2019年江蘇卷第15題)如圖1所示，質量相等的物塊A和B疊放在水平地面上，左邊緣對齊。A與B、B與地面間的動摩擦因數均為μ。先敲擊A，A立即獲得水平向右的初速度，在B上滑動距離L后停下。接著敲擊B，B立即獲得水平向右的初速度，A、B都向右運動，左邊緣再次對齊時恰好相對靜止，此后兩者一起運動至停下。最大靜摩擦力等于滑動摩擦力，重力加速度為g。求：

(1)A被敲擊后獲得的初速度大小vA；

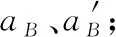
(3)B被敲擊后獲得的初速度大小vB。

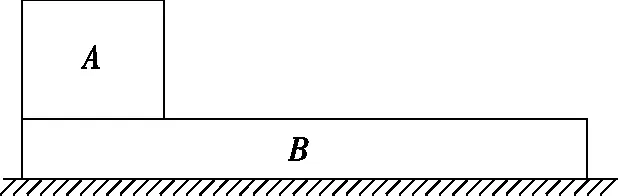
圖1

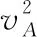
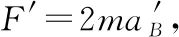
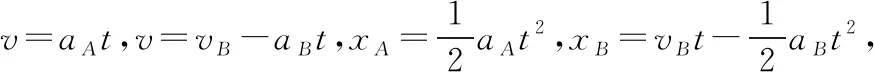
【點評與拓展】解決力學問題的三大觀點分別是動力學觀點、能量觀點、動量觀點，而本題是同一水平面內的滑塊、滑板類問題，且系統受到外力(此題是地面施加的摩擦力)，外力不為零，所以在選擇解題規律時不能選用動量守恒定律，而二者的加速度不同，故優先隔離分析選用動力學方法比較方便。

與此題類似的幾種常見的位于同一個平面內的滑塊、滑板類問題如下：(滑塊質量為m，滑板質量為M，滑板長度為L)

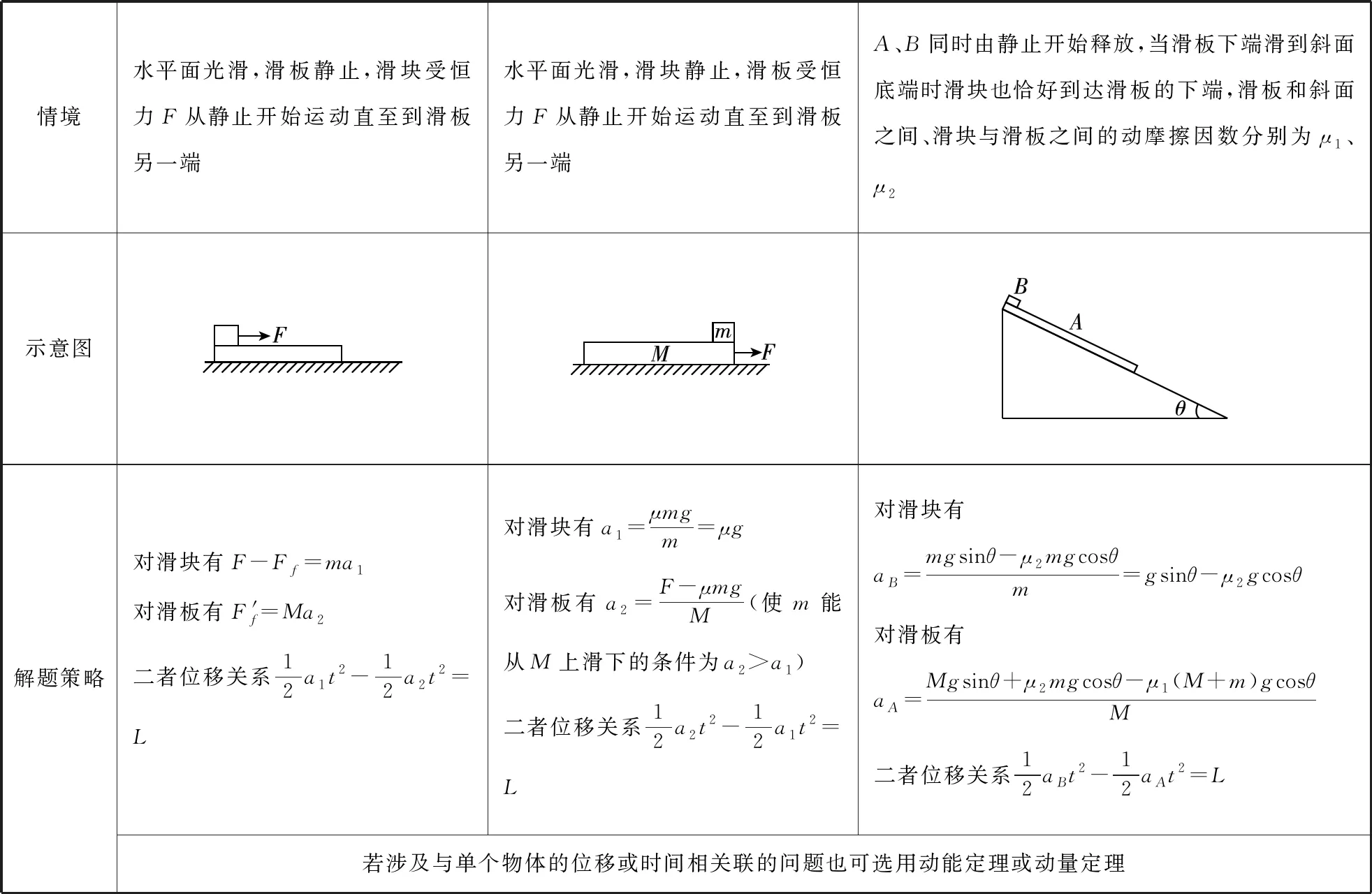
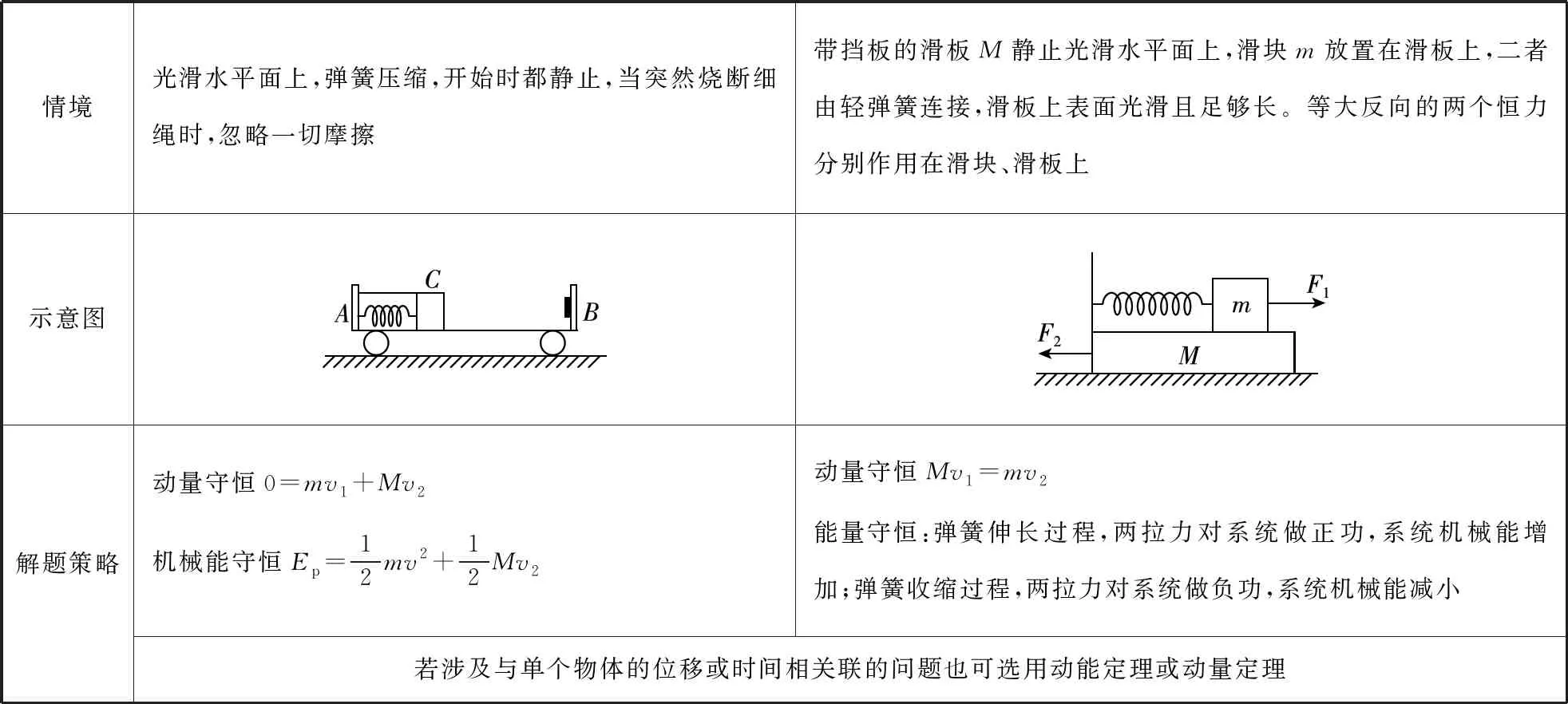
情境水平面光滑,滑板靜止,滑塊受恒力F從靜止開始運動直至到滑板另一端水平面光滑,滑塊靜止,滑板受恒力F從靜止開始運動直至到滑板另一端A、B同時由靜止開始釋放,當滑板下端滑到斜面底端時滑塊也恰好到達滑板的下端,滑板和斜面之間、滑塊與滑板之間的動摩擦因數分別為μ1、μ2示意圖解題策略對滑塊有F-Ff=ma1對滑板有Ff'=Ma2二者位移關系12a1t2-12a2t2=L對滑塊有a1=μmgm=μg對滑板有a2=F-μmgM(使m能從M上滑下的條件為a2>a1)二者位移關系12a2t2-12a1t2=L對滑塊有aB=mgsinθ-μ2mgcosθm=gsinθ-μ2gcosθ對滑板有aA=Mgsinθ+μ2mgcosθ-μ1(M+m)gcosθM二者位移關系12aBt2-12aAt2=L若涉及與單個物體的位移或時間相關聯的問題也可選用動能定理或動量定理

若母題中B與地面間的摩擦忽略不計，由于系統不受外力，則可以系統為研究對象，優先選用動量守恒和能量守恒解決較為方便，如下變式一。

【變式一】無外力作用的滑塊、滑板

【例1】如圖2所示，在光滑水平面上放置一個質量分布均勻的長木板，質量M=2 kg，板長L=1 m。一個與木板質量相同的小滑塊C(看成質點)，以水平初速度v0=4 m/s從木板的左端滑上木板，滑塊恰好能滑到木板的右端。現將木板分成質量相等的A、B兩塊并排放置，滑塊仍以v0從木板A的左端滑上木板，如圖3所示，重力加速度取g=10 m/s2。求：

圖2

圖3

(1)滑塊C與木板間的動摩擦因數μ；

(2)當滑塊C滑過A時，C與A的速度大小(結果可用根號表示)；

(3)滑塊C相對B板靜止時位于B板何處？

【解析】(1)設滑塊C質量為m，C滑到木板右端時的速度為v

由動量守恒定律可知

mv0=(m+M)v①

由能量守恒定律可知

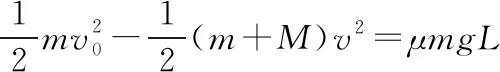
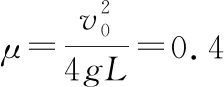
(2)滑塊C剛滑過A時的速度為v1，此時A、B兩木板速度相等均為v2，則有

mv0=mv1+Mv2③

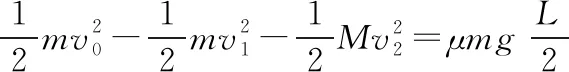
解③④式取合理值得

(3)設C相對于木板B向右滑行s后與B共速為vBC，則有

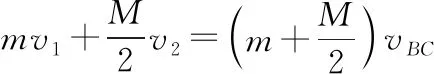
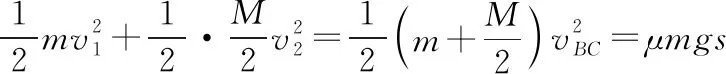
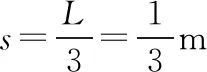
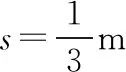
【點評與拓展】本題是同一水平面內的滑塊、滑板問題，且系統所受外力為零，故可優先采用動量守恒定律解決。解決這類問題的關鍵點有兩個：一是要找準過程中的臨界狀態點；二是要注意應用能量守恒定律，尤其是摩擦生熱的相關結論。與此題相類似的幾種常見的無外力的滑塊、滑板類問題如下：(滑塊質量為m，滑板質量為M，滑板長度為L)

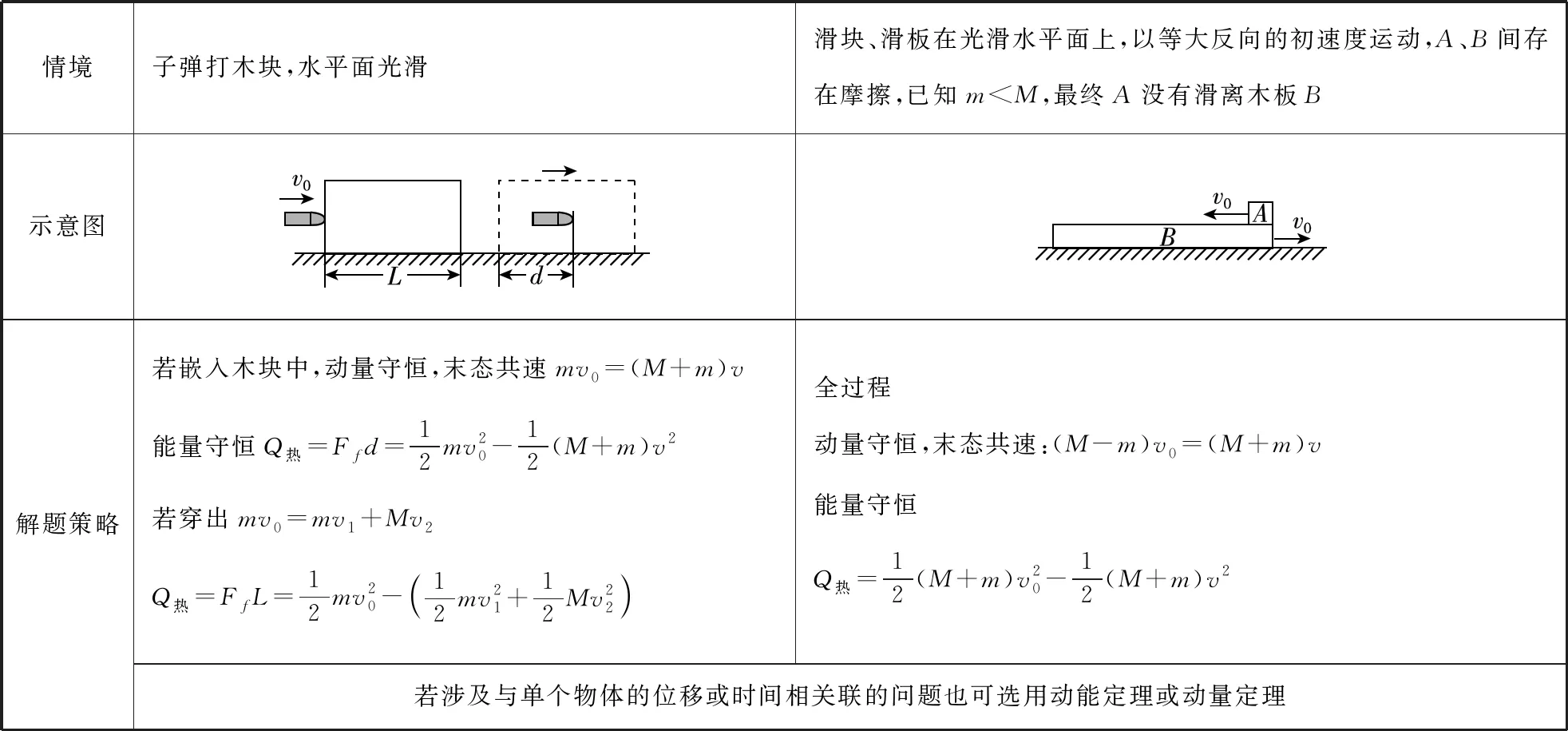
情境子彈打木塊,水平面光滑滑塊、滑板在光滑水平面上,以等大反向的初速度運動,A、B間存在摩擦,已知m

若地面摩擦、滑塊滑板間摩擦均不計，滑板由平面直板轉化為曲面或斜面，則可演變成變式二。可優先選用水平方向動量守恒定律、機械能守恒定律，如下變式二。

【變式二】滑塊+曲面(斜面)滑板問題

【例2】(2019年吉林模擬)如圖4所示，形狀完全相同的光滑弧形槽A，B靜止在足夠長的光滑水平面上，兩弧形槽相對放置，底端與光滑水平面相切，弧形槽高度為h，A槽質量為2m，B槽質量為M。質量為m的小球，從弧形槽A頂端由靜止釋放，重力加速度為g，求：

圖4

(1)小球的最大速度；

(2)若小球從B上滑下后還能追上A，求M，m間所滿足的關系。

【解析】(1)小球到達弧形槽A底端時速度最大。設小球到達弧形槽A底端時速度大小為v1，槽A的速度大小為v2。

小球與弧形槽A組成的系統在水平方向動量守恒，以水平向右為正方向，小球下滑過程中，由動量守恒定律得

mv1-2mv2=0

由機械能守恒定律得

(2)小球沖上弧形槽B后，上滑到最高點后再返回分離，設分離時小球速度反向，大小為v3，弧形槽B的速度為v4。整個過程二者水平方向動量守恒，則有

mv1=-mv3+Mv4

二者的機械能守恒，則有

小球還能追上A，則有v3>v2

解得M>3m

【點評與拓展】此類問題屬于滑塊與斜面、曲面板的組合情境，且小球從槽A上下滑和沖上槽B的過程，系統水平方向不受外力，故系統水平方向動量守恒，但系統總動量不守恒，同時，由于沒有摩擦，故系統的機械能也守恒。特別注意：當滑塊滑向滑板到達最高點時二者水平方向共速，且滑塊豎直方向的速度為零；若滑塊飛出滑板，則滑塊將做斜拋運動。若滑塊與滑板間有摩擦，則可以選用能量守恒解決。與此題相類似的幾種情境及解題策略如下。

情境質量為m的滑塊從A點由靜止釋放,最終相對靜止于B、C之間的D點(圓弧AB面光滑,半徑為R,BC面粗糙,水平地面光滑,滑板質量為M)質量為m的滑塊B從質量為M的滑板A的右端以水平初速度v0滑上滑板A,滑塊B滑到滑板A的左端并沿著圓弧部分上滑一段弧長后返回,最終停止在滑板A上(圓弧面光滑,PQ面粗糙,水平地面光滑)質量為m的滑塊從A點正上方某處無初速度下落,恰好落入質量為M的小車圓弧軌道滑動,然后沿水平軌道滑至軌道末端C處恰好沒有滑出(圓弧面光滑,BC面粗糙,水平地面光滑)示意圖解題策略A到B過程:系統動量不守恒,水平方向動量守恒,有0=mv1+Mv2系統機械能守恒mgR=12mv21+12Mv22B到C過程:系統動量守恒,有mv1+Mv2=(m+M)v系統能量守恒:Q熱=12mv21+12Mv22-12(m+M)v2全過程系統水平方向動量守恒mv0=(m+M)v全過程系統能量守恒Q熱=12mv20-12(m+M)v2從開始下落至B:軌道不動,受豎直墻壁施加的外力,系統動量不守恒,滑塊機械能守恒,有mgh=12mv20BC段:系統動量守恒,有:mv0=(m+M)v對全過程能量守恒,有Q熱=mgh-12(m+M)v2若涉及與單個物體的位移或時間相關聯的問題也可選用動能定理或動量定理

若滑板與地面間摩擦、滑塊滑板間摩擦均不計，滑塊與滑板之間利用彈簧進行相互作用，可優先選用動量守恒定律、能量守恒或機械能守恒定律，如下變式三。

【變式三】滑塊+帶彈簧的滑板情境

【例3】如圖5所示，在光滑的水平面上靜止放一質量為2m的木板B，木板表面光滑，右端固定一輕質彈簧。質量為m的木塊A以速度v0從板的左端水平向右滑上木板B，求：

圖5

(1)彈簧的最大彈性勢能；

(2)彈簧被壓縮直至最短的過程中，彈簧給木塊A的沖量；

(3)當木塊A和木板B分離時，木塊A和木板B的速度。

【解析】(1)彈簧被壓縮到最短時，木塊A與木板B具有相同的速度，此時彈簧的彈性勢能最大。設共同速度為v，從木塊A開始沿木板B表面向右運動至彈簧被壓縮到最短的過程中，A、B系統的動量守恒，取向右為正方向，則有

mv0=(m+2m)v

由機械能守恒可知，彈簧的最大彈性勢能

(2)對木塊A，根據動量定理得I=mv-mv0，解得

(3)從木塊A滑上木板B直到二者分離，系統的機械能守恒，設分離時A、B的速度分別為v1和v2，根據動量守恒定律有mv0=mv1+2mv2

【點評與拓展】對于通過彈簧連接的滑塊滑板問題，因彈力做功的過程中彈力是個變力，所以解決這類問題時，要細致分析彈簧的變化過程，抓住彈簧特殊狀態的特征，如彈簧壓縮最短(或拉伸最長)時二者共速，且此時彈性勢能最大；若系統只受彈力作用，當彈簧處于原長時速度最大或最小。對兩個狀態限定的過程優先選用系統動量守恒和能量守恒求解較為方便。

與此類似的幾種常見的通過彈簧連接的滑塊、滑板問題策略如下。(滑塊質量為m，滑板質量為M，滑板長度為L)

情境光滑水平面上,彈簧壓縮,開始時都靜止,當突然燒斷細繩時,忽略一切摩擦帶擋板的滑板M靜止光滑水平面上,滑塊m放置在滑板上,二者由輕彈簧連接,滑板上表面光滑且足夠長。等大反向的兩個恒力分別作用在滑塊、滑板上示意圖解題策略動量守恒0=mv1+Mv2機械能守恒Ep=12mv2+12Mv2動量守恒Mv1=mv2能量守恒:彈簧伸長過程,兩拉力對系統做正功,系統機械能增加;彈簧收縮過程,兩拉力對系統做負功,系統機械能減小若涉及與單個物體的位移或時間相關聯的問題也可選用動能定理或動量定理