基于意義聯結，助推思維進階

劉霞

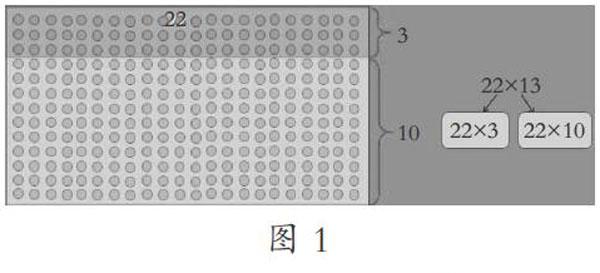
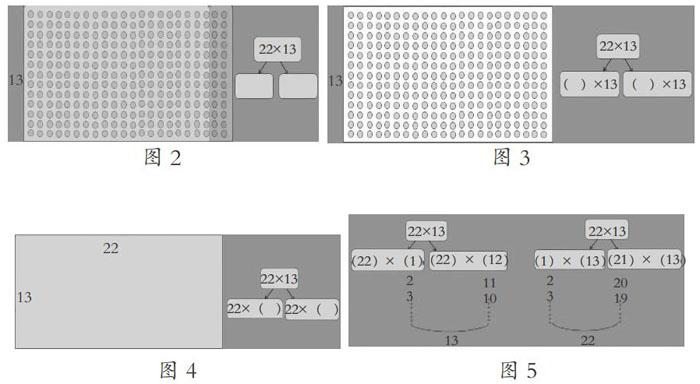
一、思維生長點：從計數走向計量，幾何直觀支撐計數單位到計量單位的轉換

三年級學生的思維能力處于從具體到抽象過渡的初期，也是思維進階的轉折點，此時幾何直觀更有利于學生進行知識的關聯溝通。設計如下的對比體驗素材，讓學生經歷關聯教學過程，鍛煉思維能力。

【題組1】

問題：一共有多少個雞蛋？（圖略）先估一下，再寫出算式，用豎式幫助解答。

追問1：為什么列出乘法算式？

追問2：擺豎式的時候，先算的是什么，再算的是什么？（豎式略）

追問3：結合圖形說一說你對這個乘法算式意義的理解。

追問4：13、22分別表示什么，286表示的是什么？

追問5：3×22=66和10×22=220分別表示什么？請在圖上圈出來，并說一說。

【題組2】

問題：這個盒子的面積是多少？（圖略）請寫出算式，并借助豎式解答。

追問1：為什么列出乘法算式？

追問2：擺豎式的時候，先算的是什么，再算的是什么？（豎式略）

追問3：你能結合圖形說一說對這個乘法算式意義的理解嗎？

追問4：一個小正方形的面積是多少？13指的是什么？22指的是什么？286表示的是什么？

追問5：3×22=66和10×22=220分別表示什么？請在圖上圈出來，并說一說。

對比追問：不變的是什么，變的是什么？

兩份對比素材，分別是點狀的雞蛋圖和面狀的格子圖。每份素材設計相似的問題，每個問題都承載了各自的設計意圖。追問1：倒逼學生思考乘法的意義和本質，從乘法意義的角度進行思考，一個是計數單位的累加，一個是計量單位的累加，都是求積的過程。追問2：從意義出發關聯算理。……