改編常規(guī)習題 撬動思維發(fā)展
——《長方形和正方形周長復習》練習設(shè)計與教學實施

俞國芳

復習課，不是習題的堆砌，也不是簡單的重復。教師應選擇有利于學生思維投入的練習，讓復習課也具有生長的力量。練習設(shè)計并非要另辟蹊徑，教材中的常規(guī)習題蘊藏著豐富的學習資源，充分挖掘、合理利用常規(guī)習題是有發(fā)展力的學習素材。筆者以《長方形和正方形周長的復習》為例，談一談如何改編常規(guī)習題，培養(yǎng)學生能力。

一、改變數(shù)據(jù)，從少到多，培養(yǎng)思維的發(fā)散性

《長方形和正方形》是人教版第五冊第七單元的學習內(nèi)容，是學習平面圖形的基礎(chǔ)，重在理解周長的意義。教材配套作業(yè)本（浙江教育出版社）中有如下練習：“兩個長8 厘米、寬4 厘米的長方形可以拼成怎樣的圖形？這個圖形的周長是多少厘米？”學生可以得出如下結(jié)論：

解答：（8×2+4）×2=40（厘米）

解答：（8+4×2）×2=32（厘米）

解答：（8+8+4）×2=40（厘米）

練習課中的重點是關(guān)注長方形周長的計算，而復習課不僅需要鞏固周長的計算，還要拓展學生的解題思路、多角度地考慮問題，使學習更深入。

【改編】三個長是8 厘米、寬是4 厘米的長方形可以拼成怎樣的圖形？ 周長是多少？

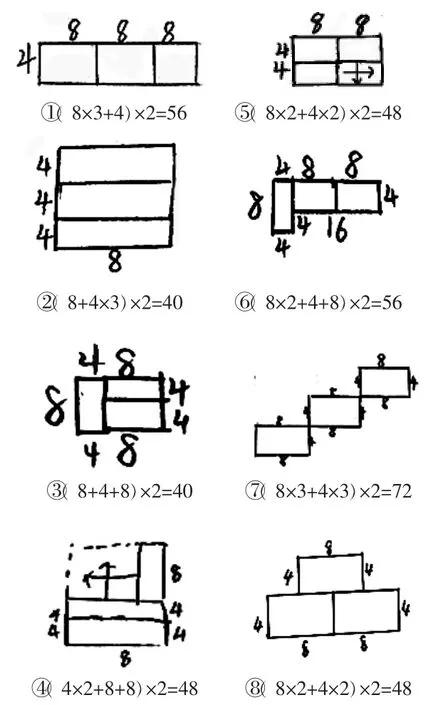
三個長方形可以拼出更多不同的圖形，通過數(shù)據(jù)的改變，將習題變得更為開放。從解答情況反映出學生思維層次與學習態(tài)度的不同。全班11%的學生寫出2 種拼法，有68%的學生能寫出3 種拼法，有21%的學生寫出了4 種及以上拼法。

師：拼成的圖形形狀不同，為什么有些圖形的周長相同？

生：②③這兩個圖形重疊的邊都是長邊，所以周長都比3 個分開的長方形少了4 個8 厘米。

生：兩個圖形重疊部分相同，周長也會減少相同的部分，所以周長相同。

師：三個長方形怎樣拼周長最長？怎樣拼周長最短？

生：圖形之間重疊的部分越多，周長越短；重疊部分越少，周長越長。

數(shù)據(jù)的改變增加了圖形拼組的情況，學生不僅鞏固了周長的計算、平移知識，還從相同的答案中發(fā)現(xiàn)周長不變的原因，得出了拼組后圖形周長的多種計算方法。學生的知識得到鞏固，思維得到了發(fā)散。

二、拓展認知，從特殊到一般，培養(yǎng)思維的深刻性

當學生遇到有分歧的觀點，或得到的結(jié)果與自己當前的理解有差異時，就會產(chǎn)生認知沖突。認知沖突的解決會讓學生學到新的知識，提高理解水平。課本88 頁有如下練習：

下圖的長方形分成兩個部分，哪個部分的周長長？

90%的學生第一感覺認為兩個圖形的周長不同，教師引導學生思考圖形的周長，描一描圖形的邊線，學生發(fā)現(xiàn)兩部分圖形有一條公共邊，是兩條相等的邊，所以圖形的周長相等。學生在此基礎(chǔ)上，還設(shè)計出很多周長相等的兩部分。

為使學生對周長的理解更到位，認識更深入，筆者在復習課上將長方形改成三角形，將特殊圖形改成一般圖形，檢驗學生對周長比較的認識。【改編】將下圖的三角形分成兩個周長相等的圖形。

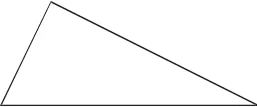
受已有知識和經(jīng)驗的負遷移，全班有89.2%學生將三角形一條邊對分，如圖①、圖②、圖③；21.6%的學生認為三角形的邊有長短，分成兩個底邊長短不一的三角形，如圖④、圖⑤；僅10.2%的學生量出三角形三條邊的長度，將三角形分成了周長相等的兩部分，如圖⑥。

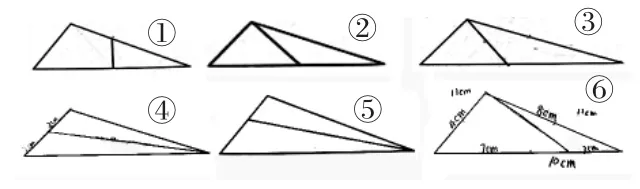
教師引導學生對比思考圖①、圖②、圖③。

師：你是怎么分的？周長相等嗎？

生：長方形的中點連一連，分成的兩部分周長是相等的。我找到一條邊的中點連起來，作為一條公共邊，這樣三角形的兩部分也相等。

生：周長相等的兩部分除公共邊外，另外的幾條邊也要相等，圖①、圖②、圖③的兩個圖形的邊是不相等的。

教師引導學生對比思考圖②、圖⑤、圖⑥的周長，明白要使圖形周長相等，必須要所有邊的長度總和相等。學生意識到不能像圖⑤這樣隨意畫，需要量出三角形三條邊的長度。

師：知道三條邊的長度該怎樣連線才能將三角形分成兩個周長相等的圖形？

生：除了公共邊，我們也要想辦法讓剩下的邊長度相等。

生：三角形三條邊長度不同，我把它平均分成兩部分，再連線，就可以得出周長相等的圖形了。

分成兩個周長相等的三角形：

分成兩個周長相等的圖形：

認識事物總是從特殊到一般，從而發(fā)現(xiàn)事物的本質(zhì)屬性，發(fā)現(xiàn)事物存在的普遍規(guī)律。通過練習，進一步使學生明白兩部分周長相等需要所有的邊相等，與正方形、長方形分成周長相等的兩部分本質(zhì)上是相同的，溝通了方法上的聯(lián)系，真正從概念的本質(zhì)理解問題、解決問題。

三、打破慣性，從常規(guī)到非常規(guī)，培養(yǎng)思維的靈活性

史寧中教授說：“創(chuàng)新能力來自知識積累、經(jīng)驗積累和思維訓練。”長方形周長在生活中應用廣泛，教師有意識地選擇生活與數(shù)學相聯(lián)系的練習，幫助學生鞏固知識技能，增強實際應用能力。

例：一塊長方形菜地，長6米，寬3 米。四周圍上籬笆，籬笆長多少米？如果一面靠墻，籬笆至少要多少米？

這是教材第88 頁的練習，意在鞏固周長的計算，能運用周長的知識解決實際生活問題。將菜地一面靠墻，這是生活中常見的方法，可以節(jié)約材料。學生在解決問題時提出兩種可能：長邊靠墻：6+3×2=12（米）；短邊靠墻：6×2+3=15（米），通過圖示表達，也比較容易解決。復習課上，我們將這一材料加以改編，在此基礎(chǔ)上提出新的問題：

【改編】養(yǎng)雞專業(yè)戶李伯伯要新建一座長方形雞舍，雞舍長23米，寬15 米。

（1）建這個雞舍需要多少米的材料？

（2）李伯伯為了節(jié)約材料，想靠墻建雞舍，墻長20 米。要怎樣建最好？ 此時籬笆的周長是多少米？（畫圖分析并計算）

第一個問題是基礎(chǔ)，學生利用長方形周長的計算方法可以得出建雞舍需要（23+15）×2=76（米）。第二個問題改變原有教材表述（教材習題沒有說明墻的長度），給予的信息是墻只有20 米，給解決問題設(shè)置了限定。

解一：（20+15）×2=70（米）。

生：這道題我做錯了，我想著墻只有20 米，雞舍也只能建20米長。但我計算了周長后忘記減去利用墻做籬笆的那段長度。（比例：5.4%）

解二：23+15+15=53（米）。

生：雞舍靠墻建設(shè)比較節(jié)約材料，可以長邊靠墻，也可以短邊靠墻，所以我就選了長邊靠墻更節(jié)約。但是沒有考慮到墻只有20米。（比例：2.7%）

解三：2×23+15=61（米）。

生：墻只有20 米，李伯伯要建長23 米的雞舍，長的一邊靠墻不夠，所以就用短的一邊靠墻，這樣周長最短。（比例：81.1%）

解四：15×2+23+3=56（米）。

生：墻20 米，雞舍的長要23米，是不夠長的，如果把短邊靠墻，可以節(jié)約15 米的材料，如果長邊靠墻，可以節(jié)約23 米。雖然不夠，我補3 米，這樣還是比短邊靠墻要節(jié)約。（比例：10.8%）

81.1%的學生認為長邊靠墻不夠，就只能短邊靠墻，只有10.8%的學生想到只要補上長邊不夠的那部分籬笆，也可以利用墻的長度來建設(shè)雞舍。特殊的設(shè)計方法給學生“豁然開放”的感覺。

練習的改編設(shè)計，使思維敏捷、有開拓精神的學生找到了展示的舞臺。經(jīng)過方法討論，讓其他學生打破了原有的固定思維，形成新的思考方式，也獲得了更優(yōu)化的解決問題的途徑和方法。這是學生在今后學習和生活中的一種創(chuàng)新能力的需要，通過習題的設(shè)計可以逐步培養(yǎng)學生“逆向思維、非常規(guī)思維”，提高學生解決問題的能力。

不同的學生能力有差異，復習課不僅鞏固了知識還提升了學生綜合能力。教師在選擇練習材料時，需要充分考慮不同層次學生的發(fā)展需要，在能力要求、解決策略、思維表達上都能有梯度的設(shè)計，讓不同的學生有不同的發(fā)展。