『學(xué)會思維』導(dǎo)向的課堂教學(xué)策略
徐志彤
思維能力是一切智能活動的核心。《數(shù)學(xué)課程標(biāo)準(zhǔn)(2011年版)》指出:數(shù)學(xué)教學(xué)活動,特別是課堂教學(xué)應(yīng)激發(fā)學(xué)生興趣,引發(fā)學(xué)生的數(shù)學(xué)思考,掌握數(shù)學(xué)的基本思想和思維方式。以“學(xué)會思維”為導(dǎo)向,進(jìn)行小學(xué)數(shù)學(xué)課堂教學(xué)改革,致力于學(xué)生學(xué)科核心素養(yǎng)的培養(yǎng),對學(xué)生未來發(fā)展具有重要意義。
一、“學(xué)會思維”導(dǎo)向的課堂實踐模型
為了更好地引導(dǎo)學(xué)生“學(xué)會思維”,促進(jìn)學(xué)科核心素養(yǎng)提升,我們嘗試構(gòu)建了“‘學(xué)會思維’導(dǎo)向的課堂實踐模型”,如下圖所示:
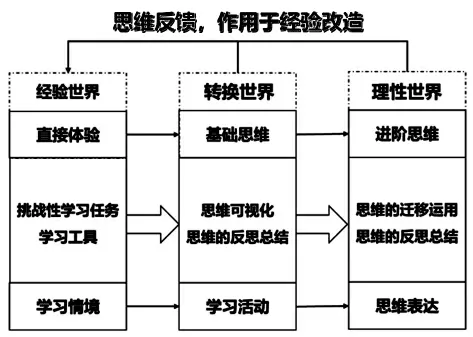
第一階段是學(xué)生進(jìn)行直接體驗的階段。學(xué)生依托真實的學(xué)習(xí)情境,在挑戰(zhàn)性學(xué)習(xí)任務(wù)的驅(qū)動下,采用豐富的學(xué)習(xí)工具與資源,借助基礎(chǔ)知識與技能的有效學(xué)習(xí),形成對外部世界的直接體驗。
第二階段是學(xué)生構(gòu)建基礎(chǔ)思維的階段。學(xué)生在學(xué)習(xí)活動過程中,已初步形成了一些基礎(chǔ)思維,利用思維可視化工具,一方面利于教師了解學(xué)生的思維狀態(tài),及時調(diào)整教學(xué)策略;另一方面學(xué)生利用思維可視化工具,在思維表達(dá)的過程中進(jìn)行思維的重組和整合,以利于思維的躍遷,從基礎(chǔ)思維向進(jìn)階思維邁進(jìn)。
第三階段是學(xué)生形成進(jìn)階思維的階段。學(xué)生借助思維表達(dá),在豐富的解決問題過程中,進(jìn)行思維的反復(fù)遷移運用,并對思維運用進(jìn)行反思總結(jié),從而形成牢固的進(jìn)階思維體系,這種思維體系反過來也能作用于經(jīng)驗改造,實現(xiàn)思維反饋。
二、“學(xué)會思維”導(dǎo)向的課堂教學(xué)策略
1.創(chuàng)設(shè)能引發(fā)學(xué)生思考的任務(wù)情境,讓“學(xué)會思維”成為可能。
“學(xué)會思維”導(dǎo)向的課堂教學(xué)的實施,首要條件是創(chuàng)設(shè)能引發(fā)學(xué)生思考的任務(wù)情境。任務(wù)情境要以精妙、精當(dāng)和真實的數(shù)學(xué)問題的整合設(shè)計呈現(xiàn)。因此,情境中所揭示的問題必須具備以下四個特征:
(1)問題設(shè)計要聯(lián)系實際,具有真實性。與學(xué)生生活經(jīng)驗相契合,能充分激發(fā)學(xué)生學(xué)習(xí)興趣,調(diào)動學(xué)生學(xué)習(xí)積極性,還能讓學(xué)生感受到數(shù)學(xué)學(xué)習(xí)的意義和價值。
(2)問題設(shè)計要有明確指向,具有目標(biāo)性。情境中的問題要清晰具體指向本節(jié)課需要達(dá)成的知識、能力、思維發(fā)展目標(biāo),揭示具有數(shù)學(xué)本質(zhì)的學(xué)習(xí)任務(wù),讓學(xué)生明白“做什么”“怎么做”。
(3)問題設(shè)計要有思維含量,具有挑戰(zhàn)性。要讓學(xué)生“學(xué)會思維”,問題設(shè)計就要跨越記憶、淺層次理解的范疇,走向應(yīng)用、分析、綜合和評價的領(lǐng)域。
(4)問題設(shè)計可采用“1+X”的學(xué)科問題設(shè)計思路。任務(wù)情境中的問題可以是單個的,也可以采用“1+X”的設(shè)計思路,將一類子問題圍繞核心問題進(jìn)行序列化呈現(xiàn)。
2.提供豐富的學(xué)習(xí)工具與資源,讓學(xué)生在實踐體驗中獲得經(jīng)驗性理解。
(1)基于生活,喚醒學(xué)生已有經(jīng)驗儲備。喚醒這些經(jīng)驗儲備將有利于幫助學(xué)生順利進(jìn)入新知識經(jīng)驗的輸入和加工。具體操作過程中,教師可以用問題引導(dǎo)學(xué)生回憶已經(jīng)學(xué)過的知識和掌握的方法,將學(xué)生已有的“前理解”結(jié)構(gòu)顯性化。也可以精心設(shè)計知識的呈現(xiàn)方式和組織形式,直接在解決問題中激活學(xué)生已有認(rèn)知。
(2)豐富資源,采用不同學(xué)習(xí)方式體驗探索。教師要提供豐富的學(xué)習(xí)資源,保障學(xué)生能采用適當(dāng)?shù)膶W(xué)習(xí)方式開展體驗探索,積累豐富的經(jīng)驗性理解。學(xué)習(xí)資源可以是各類操作學(xué)具、《學(xué)習(xí)單》(表),也可以是音視頻材料和網(wǎng)絡(luò)資源,教師和學(xué)生本身也是非常好的學(xué)習(xí)資源,在對話交流中能幫助他人啟智明理。在為學(xué)生提供學(xué)習(xí)資源時要做到三點:一是要為每一個學(xué)生提供不同的資源以供其選擇;二是工具、資源的設(shè)計要滿足不同層次學(xué)生發(fā)展的需要;三是體驗探索的方式很多,觀察、模仿、傾聽、思考、討論、動手做數(shù)學(xué)實驗等都是好方法,教師要充分尊重并給予支持。
3.聚焦數(shù)學(xué)本質(zhì),在思維可視化過程中發(fā)展基礎(chǔ)性思維。
(1)思維可視化的意義。學(xué)生通過實踐體驗獲得的經(jīng)驗性理解,往往具有內(nèi)隱、零散、模糊的特點。思維可視化能將這些經(jīng)驗形式化表達(dá)出來。形式化表達(dá),首先需要學(xué)生在頭腦中加工,即對知識經(jīng)驗分類、比較、抽象、概括;其次需要學(xué)生選擇合適的方法進(jìn)行輸出。“加工——輸出”的過程在感性認(rèn)識和理性思考間架起橋梁,對發(fā)展學(xué)生基礎(chǔ)性思維具有重要意義。
(2)思維可視化的作用。借助可視化工具呈現(xiàn)學(xué)生的思維過程及結(jié)果,主要作用體現(xiàn)在兩個方面:一是能將孤立零散的知識經(jīng)驗以整合的、情境化的形式納入原有認(rèn)知結(jié)構(gòu),不僅便于理解掌握,更利于調(diào)用遷移;二是搭建分享對話的平臺,讓學(xué)生能最大限度地理解交流,在表達(dá)中深化認(rèn)識,在比較中調(diào)整改造,在辨析中去粗存精。
(3)思維可視化的方法。主要有兩種方式:一是言語表達(dá),這是學(xué)生最主要、最直觀的可視化方式,因此要讓學(xué)生學(xué)會清晰準(zhǔn)確地表達(dá);二是符號、圖示表達(dá),利用符號、圖示可以表達(dá)一個內(nèi)容的思考過程與結(jié)果。利用符號、圖示還可以呈現(xiàn)知識經(jīng)驗間的相互聯(lián)系,表示關(guān)系的工具通常采用思維導(dǎo)圖,不同的思維導(dǎo)圖能促進(jìn)不同思維能力的發(fā)展。
4.在不斷遷移運用中建立聯(lián)系、固化方法,幫助學(xué)生形成理性思維。
(1)在“起承轉(zhuǎn)合”中變換思維視角。學(xué)生應(yīng)通過具體的學(xué)習(xí)促進(jìn)自身思維的發(fā)展,特別是,應(yīng)當(dāng)不斷提升自身思維的品質(zhì)。在綜合運用基礎(chǔ)性思維解決陌生和不確定問題時,學(xué)生需要廣泛地聯(lián)想、檢索信息,并做出解釋判斷,過程中需要養(yǎng)成不斷變換思維視角的習(xí)慣,提升思維品質(zhì)。所謂“起”,即面對具體問題能多樣化表征,并找到適切的方法解決之。例如蘇教版三年級《解決問題的策略》中,“一個皮球從16 米的高處落下,如果每次彈起的高度總是它下落高度的一半,第3 次彈起多少米?第4 次呢?”面對這樣比較抽象且與例題不屬于同一種類型的新問題,學(xué)生在解決時要學(xué)會調(diào)用“列表”“畫圖”等策略進(jìn)行表征,這樣才能順利解決。所謂“承”,即能由此及彼、由易到難地聯(lián)想類推。所謂“轉(zhuǎn)”,即能化繁為簡、化難為易地進(jìn)行思考。例如《表面涂色的正方體》,要探究棱長四等分的正方體的表面涂色情況,可以從簡單想起,先轉(zhuǎn)化成2等分、3 等分正方體涂色情況的探究,然后再獲得解決復(fù)雜問題的方法。所謂“合”,即能形成自動化思維長鏈來解決挑戰(zhàn)性問題。遇到不確定問題時,學(xué)生的自動化反應(yīng)可以分為四個層面:一是判斷,對不對?看懂了嗎?二是比較,有什么相同與不同?三是聯(lián)想,還有什么調(diào)整與補(bǔ)充?四是抽象,通過研究我有什么發(fā)現(xiàn)與收獲?
(2)在“仿糾變用”中實現(xiàn)思維躍遷。所謂“仿糾變用”情境,即四個不同層次的遷移運用情境:模仿性變式——不同情境,同樣問題;糾錯性變式——錯誤情境,同樣問題;綜合性變式——復(fù)雜情境,同樣問題;運用性變式——生活情境,不同問題。例如《比和比的基本性質(zhì)》一課,在遷移運用環(huán)節(jié)可以創(chuàng)設(shè)這樣幾個層次任務(wù)情境:第一層模仿性變式,“化簡比,并求比值”,可以精選書上習(xí)題,并對部分?jǐn)?shù)據(jù)進(jìn)行微調(diào),利于學(xué)生根據(jù)數(shù)據(jù)特點選擇合適的方法化簡比、求比值;第二層糾錯性變式,可以呈現(xiàn)學(xué)生作業(yè)中的錯例,引導(dǎo)學(xué)生反思錯誤的原因,同時要努力增強(qiáng)學(xué)生在“反思”方面的自覺性,教師應(yīng)當(dāng)經(jīng)常性提及這樣三個問題:“什么?”(“現(xiàn)在在干什么”或“準(zhǔn)備干什么?”)“為什么?”(“為什么這樣做?”)“如何?”(“這樣做的實際效果如何?”)第三層綜合性變式,可以采用教材第57 頁第8 題,分別寫出每組正方形邊長和面積的比,并化簡(圖略),這一題除了要讓學(xué)生寫出邊長比、面積比,并化簡,還要引導(dǎo)學(xué)生通過運用對比發(fā)現(xiàn)正方形邊長比與面積比之間的關(guān)系,引發(fā)學(xué)生深層次思考;第四層次是運用性變式,教師可以從學(xué)生比較熟悉的生活情境入手,將比和之前學(xué)習(xí)的分?jǐn)?shù)進(jìn)行聯(lián)系,讓學(xué)生將分率和比進(jìn)行互化,同時還能將小數(shù)轉(zhuǎn)化為比,溝通知識之間的聯(lián)系,為后續(xù)學(xué)習(xí)比的應(yīng)用做好充分準(zhǔn)備。
讓學(xué)生“學(xué)會思維”是小學(xué)數(shù)學(xué)教學(xué)的核心價值追求,是落實學(xué)科育人要求、彰顯學(xué)科育人本質(zhì)的根本途徑。在“學(xué)會思維”的過程中,我們要遵循學(xué)生認(rèn)知發(fā)展的規(guī)律,堅守數(shù)學(xué)教學(xué)的規(guī)律,以數(shù)學(xué)內(nèi)容為載體,精心設(shè)計數(shù)學(xué)活動,在引導(dǎo)學(xué)生經(jīng)歷體驗、自主探索的過程中發(fā)展思維能力,優(yōu)化思維品質(zhì)。
 小學(xué)教學(xué)設(shè)計(數(shù)學(xué))2020年12期
小學(xué)教學(xué)設(shè)計(數(shù)學(xué))2020年12期
- 小學(xué)教學(xué)設(shè)計(數(shù)學(xué))的其它文章
- 把握知識關(guān)聯(lián) 實現(xiàn)整體建構(gòu)
——《平行四邊形的面積計算》教學(xué)設(shè)計與說明 - 怎樣圍面積最大
——《用列舉的策略解決問題》教學(xué)與反思 - 高效整合,讓復(fù)習(xí)課妙趣橫生
——《長方體、正方體單元復(fù)習(xí)》教學(xué)實踐與反思 - 德育在小學(xué)數(shù)學(xué)概念教學(xué)中的滲透
——以《百分?jǐn)?shù)的意義》教學(xué)為例 - 多元對比促完善 數(shù)據(jù)分析謀發(fā)展
——《條形統(tǒng)計圖》教學(xué)設(shè)計 - 繪本游戲在課堂教學(xué)中的應(yīng)用
——以《6的乘法口訣》為例
