冰棱對三維覆冰導線氣動力特性影響研究

祝 賀， 王 剛， 郭 鑫

(東北電力大學 研究生院，吉林 吉林 132000)

高壓輸電導線覆冰通常是由于空氣中的過冷卻水滴撞擊在導線上凍結，過冷水撞擊導線瞬間沒有將水滴完全凍結，部分水滴在重力和風速作用下流向導線下部并出現二次凍結，形成了獨特覆冰形態——冰棱。冰棱的產生改變了覆冰導線橫截面形狀，由穩定截面變成非穩定截面。這種橫變截面冰棱覆冰導線在風荷載作用下產生的升力和阻力可能引起導線出現低頻、大幅度舞動。輸電導線舞動會引起線路倒塔、斷線、掉串以及短路、跳閘和大面積停電等事故，給電力系統帶來重大損失，威脅電網的安全穩定運行和供電系統運行的可靠性[1-2]。

目前很多國內外學者對覆冰導線氣動失穩引起導線舞動的基本特性進行了研究，王瓊等對D形覆冰四分裂導線氣動力進行了風洞試驗研究，分析了不同導線型號、分裂間距下分裂導線的氣動力特性[3]；樓文娟等[4-5]利用風洞試驗分析了不同厚度和不同初凝角下D形覆冰分裂導線的氣動力特性；文獻[3-5]都是從導線D形覆冰角度進行研究，分析了覆冰厚度、風攻角、分裂間距等因素下覆冰導線氣動力。馬文勇等[6-7]對新月形覆冰導線進行氣動力研究，分析了覆冰導線馳振穩定性；王瓊等[8-10]通過數值模擬對新月形四分裂覆冰導線舞動特性進行研究；嚴波等[11]對新月形偏心覆冰導線進行了升力和阻力系數進行了試驗；文獻[6-11]選擇了新月形覆冰類型進行研究，通過分析分裂導線氣動力特性研究覆冰導線馳振穩定性。陳友慧等[12]對扇形覆冰導線氣動力特性進行研究，分析了扇形覆冰導線舞動特性；李新民等[13]對扇形覆冰導線進行了空氣動力學試驗研究，分析了影響覆冰導線舞動因素；文獻[12-13]考慮了扇形覆冰導線氣動力特性，分析了扇形覆冰導線發生舞動概率。以上研究都關注穩定截面覆冰導線氣動力及舞動特性，并分析了覆冰厚度、風攻角、分裂數等對其產生的影響，而忽略了非均勻橫截面覆冰導線氣動力及其相互影響對導線舞動影響。為此利用ANSYS軟件，建立三維五冰棱覆冰導線繞流場模型并進行數值模擬分析，監控冰棱覆冰導線的阻力系數、升力系數，根據Den Hartog理論計算馳振力系數，研究覆冰導線馳振穩定性。

1 流場數學模型

1.1 流體運動方程

任何流體流動都要受到物理定律的約束，連續介質模型條件下，質量守恒定律在流體流動力學中的表現形式為連續性方程，同時在模型中物質的速度和密度都可用三維坐標函數表示。其控制方程為連續性方程[14]

(1)

式中:u，v，w為速度矢量;對于不可壓縮流體，ρ為常數。

湍流現象是高度復雜，目前沒有一種模型能對所有湍流現象進行模擬，本文擬選用Fluent提供的湍流黏度考慮了湍流剪應力的SSTk-w湍流模型，其流動方程[15]

Gk-Yk+Sk

Gw-Yw+Dw+Sw

(2)

式中:Gk為湍流動能;Gw為w方程;Γk,Γw分別為k與w的有效擴散項;Yk,Yw分別為k與w的發散項。

1.2 氣動力參數計算

覆冰導線氣動力參數主要由兩方面表示，其一，覆冰導線阻力和升力；其二，無量綱參數阻力系數和升力系數。阻力系數和升力系數分別可由下式表示為[16]

CD=2FD/(ρU2LB)

(3)

CL=2FL/(ρU2LB)

(4)

式中:CD、CL分別為阻力系數和升力系數；FD為覆冰導線阻力，阻力方向以來流方向為正；FL為覆冰導線升力，升力方向以來流方向順勢針旋轉90°為正；ρ為環境空氣密度，其取值為1.225 kg/m3；U為來流風速均值，m/s；B為橫截面覆冰導線模型特征長度；L為橫截面覆冰導線模型長度。

1.3 覆冰導線橫向馳振分析

非均勻橫截面覆冰導線在風荷載作用下，產生升力和阻力導致橫截面覆冰導線出現馳振現象。由Den Hartog馳振機理，在相同風攻角下，升力系數對風攻角倒數與阻力系數的和值大于零時，振動系統不發生馳振；升力系數對風攻角倒數與阻力系數的和值小于零時，振動系統出現失穩馳振，該馳振機理可表達為[17]

(5)

式中，α為非均勻橫截面覆冰導線風攻角。

2 三維冰棱覆冰導線數值模擬分析

2.1 建立冰棱覆冰導線模型

傳統二維流場對沿導線方向均勻覆冰導線是適用的，但對于非均勻橫截面冰棱覆冰導線具有局限性，不能充分表達非均勻橫截面覆冰導線流場特性。構建三維五冰棱覆冰導線計算流場，流場長為4 m、高為4 m、寬為0.125 m，冰棱覆冰導線中心點位于三維流場中心，其xy坐標為(2,2)，距離左側邊界2 m，距離右側邊界2 m，距離上下流場壁面均為2 m，將x軸正方向設置為水平風速來流方向，將x軸正方向逆時針旋轉90°即為y軸正方向，z軸為導線長度方向即導線展向方向，三維五冰棱計算流域尺寸和坐標圖見圖1。三維五冰棱覆冰導線模型覆冰后直徑為50 mm，導線長125 mm[18]，將覆冰導線模型等長度劃分為5部分，每部分有且只有一個冰棱存在，冰凌三維形狀為圓錐形(水平切掉尖端一小部分)，相鄰冰棱間距為25 mm，冰棱長度為60 mm，冰棱覆冰導線模型尺寸圖見圖2。

2.2 數值模擬計算

利用ANSYS ICEM CFD軟件對三維五冰棱覆冰導線流場進行結構化網格劃分，流場網格總數量為1 526 846，覆冰導線周圍邊界層采用外O形網格劃分[19]；同時為保證模擬精確度，對邊界層網格進行局部加密，邊界層相鄰網格距離不大于1 mm，網格劃分見圖3。

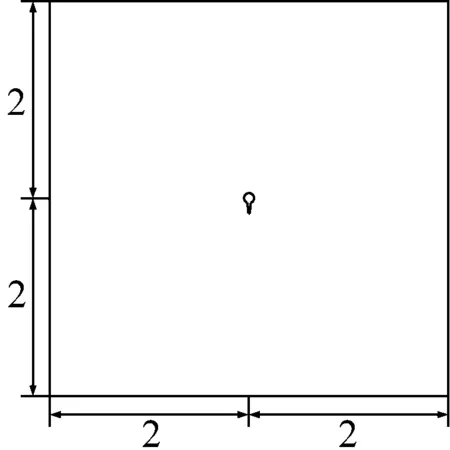
(a) 三維流域正視尺寸(m)

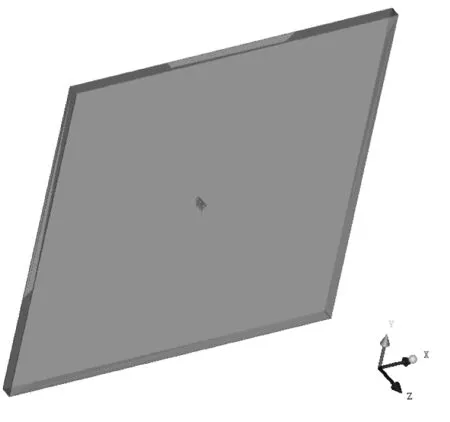
(b) 三維流域坐標

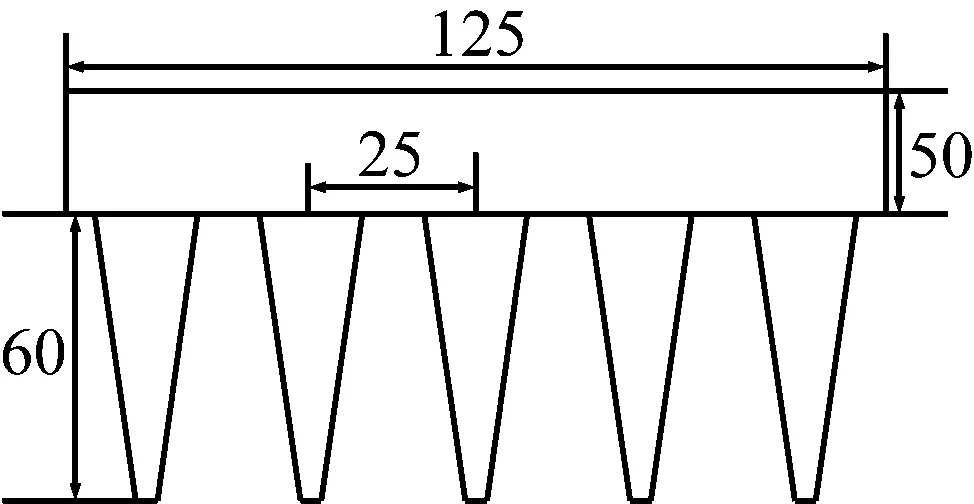
圖2 三維五冰棱覆冰導線尺寸(mm)

(a) 整體網格

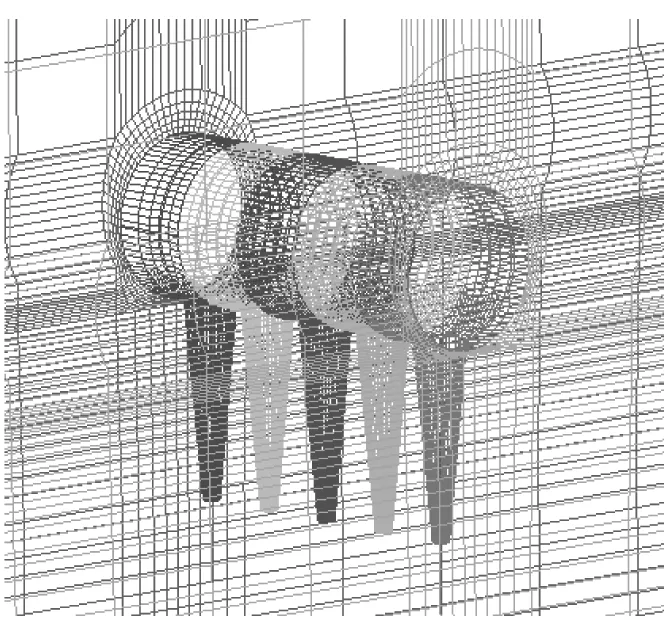
(b) 局部加密網格

為分析研究三維五冰棱覆冰導線在風場作用下氣動力及舞動特性，將冰棱覆冰導線沿z軸正方向等長度進行劃分，長為125 mm冰棱覆冰導線模型被分為5部分；每部分長為25 mm，沿z軸正方向分別編號定義為1～5[20]。為研究相鄰冰棱之間相互影響關系，在ANSYS FLUENT中選取編號為3冰棱覆冰導線節段進行氣動力參數監視，其節段劃分見圖4。

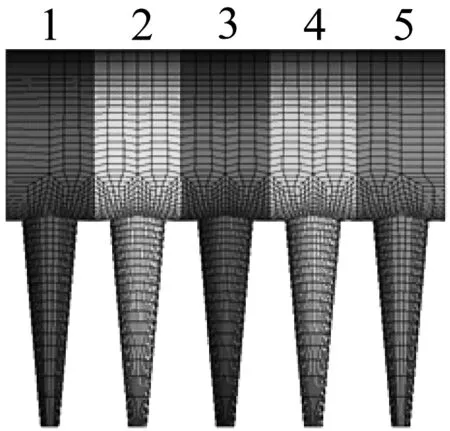
圖4 三維五冰棱覆冰導線節段

計算流域邊界條件設置：當0<α<45°時，左邊界和上邊界為風速入口，右邊界和下邊界為壓力出口；當α=45°時，左邊界為風速入口，右邊界為壓力出口；當45°<α<135°時，左邊界和下邊界為風速入口，右邊界和上邊界為壓力出口；當α=135°時，下邊界為風速入口，上邊界為壓力出口；當135°<α<180°時，右邊界和下邊界為風速入口，左邊界和上邊界為壓力出口。左右壁面均設定為對稱面(symmetry)，其余未定義壁面均默認為無滑移固面(no slip wall)，流域邊界條件設置見圖5。

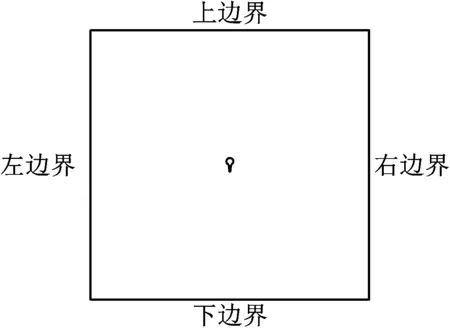
圖5 計算流域邊界條件

計算流域風攻角范圍為0°～180°，設定x軸正方向順時針旋轉45°為0°風攻角，風攻角以逆時針方向每隔10°進行一次調整。相同風攻角下分別取10 m/s、15 m/s、20 m/s、25 m/s風速進行模擬計算，時間步長為0.05，計算100步，計算流場風攻角見圖6。

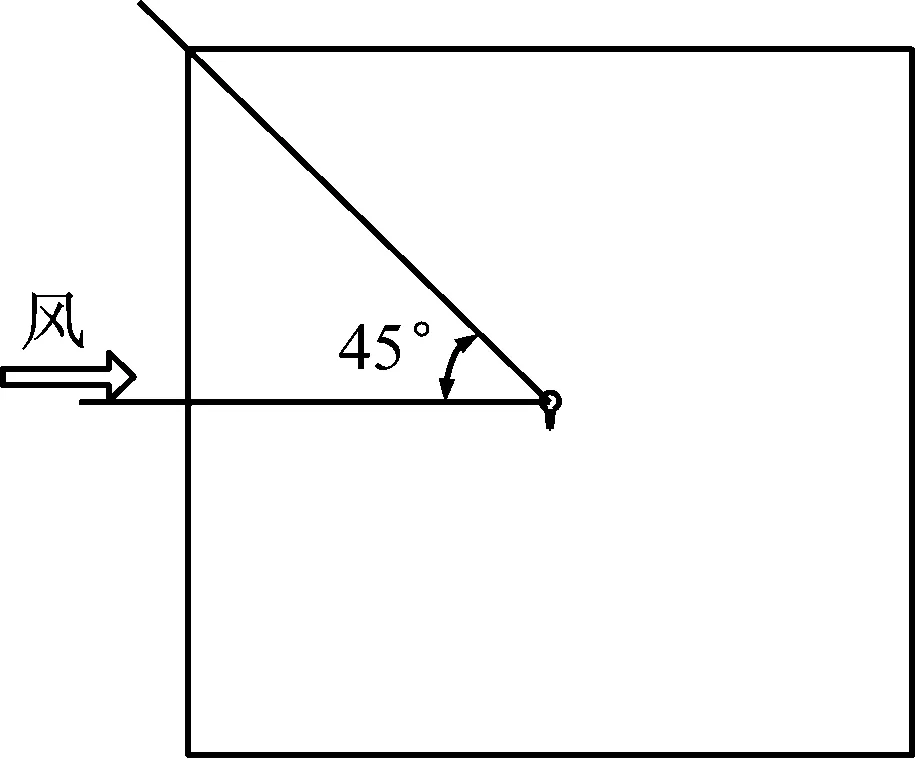
圖6 流場風攻角

3 冰棱覆冰導線氣動力數值模擬結果

3.1 冰棱覆冰導線流場特性

為研究冰棱覆冰導線表面不同位置處壓力及周圍速度特性。選取45°風攻角，來流風速為15 m/s時，不同時刻冰棱覆冰導線迎風側壓力和覆冰導線周圍速度進行分析。圖7為三維流場在45°風攻角，來流風速為15 m/s時，不同時刻覆冰導線壓力分布云圖。

由圖7可知，不同時刻迎風側壓力分布存在差異，最大壓力主要分布在圓柱迎風面下半部分和覆冰導線冰棱上半部分，最小壓力分布于覆冰導線圓柱頂部。同時可知，不同時刻圓柱與冰棱連接處壓力大小有明顯變化，在2.25 s、2.5 s時刻圓柱與冰棱連接處壓力處于最大值，其值為，在2.75～3.5 s期間連接處壓力由變為。

2.25

2.5

2.75

3.0

3.25

3.5

冰棱迎風側壓力分布呈周期性變化，在2.25～3.0 s期間，最大壓力覆蓋面積逐漸減小，在3.0～3.5 s期間，最大壓力覆蓋面積逐漸增大，在3.5 s后覆蓋面積又逐漸減小。同時最大壓力變化時冰棱迎風側壓力分布始終呈現為“圓錐面”分層分布。

圖8為三維流場在45°風攻角，來流風速為15 m/s時，節段3中心點截面不同時刻速度云圖。

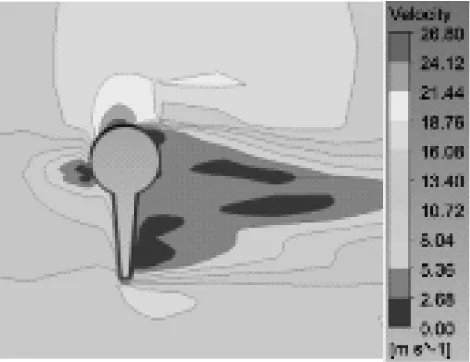
2.75

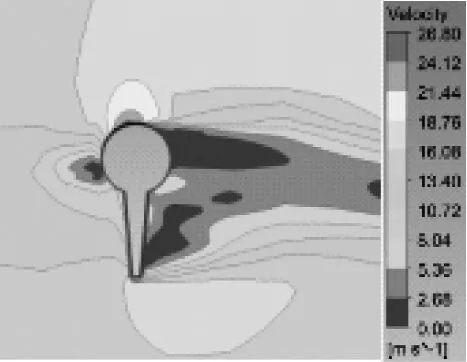
3.25

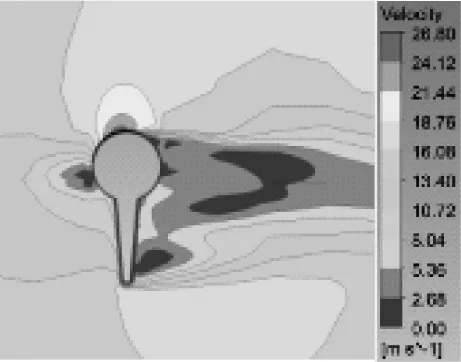
3.5

由圖8可知，不同時刻節段3截面速度分布有明顯差異，隨著時間推移冰棱底端對速度加速影響范圍逐漸增大，對背風側低速區域有明顯擠壓效應。

3.2 全攻角下冰棱覆冰導線氣動力特性分析

選取位于三維五冰棱覆冰導線模型中間節段3作為對象分析研究，圖9為節段3在不同風速和攻角下的升力和阻力系數。

由圖9可知，阻力系數隨著攻角增大，趨勢表現為先增大、后減小、再增大。在風攻角50°～60°區間取得阻力系數最大值，在風攻角130°～140°區間取得阻力系數最小值。隨著風速增加，阻力系數最大和最小值均減小，但變化幅度小。升力系數總體呈現為先減后增。在風攻角為20°時，升力系數取得最大值，且隨著風速增加，升力系數最大值增加；在風攻角為100°和170°時，升力系數取得最小值，并隨著風速增加，升力系數最小值增加。

3.3 不同因素影響冰棱覆冰導線氣動力特性

三維冰棱覆冰導線在風荷載作用下表現出來的氣動力參數特性與多種影響因素有關，考慮三維冰棱覆冰導線自身結構，分析其對覆冰導線氣動力的影響有助于分析研究冰棱覆冰導線氣動力特性。

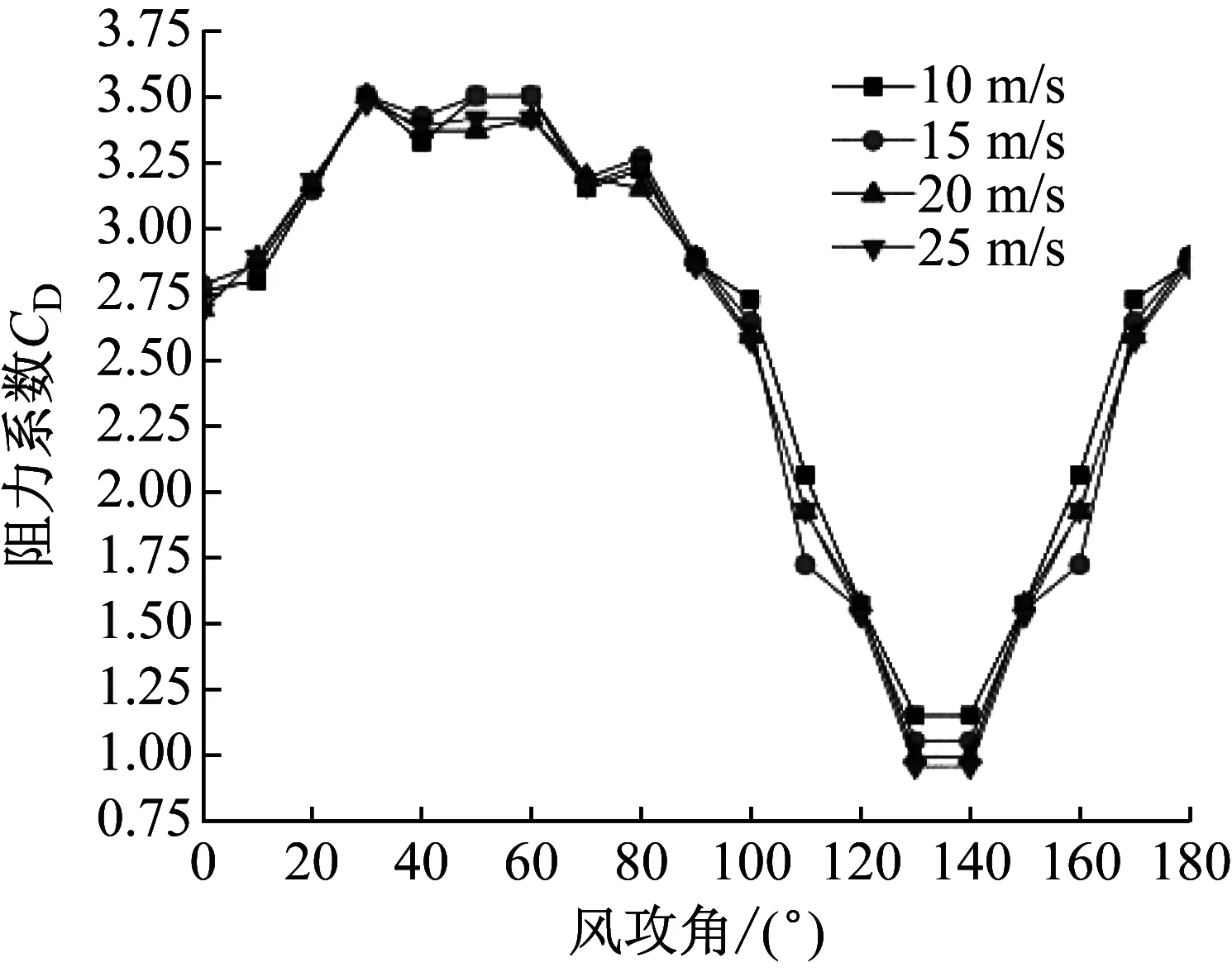
(a) 阻力系數

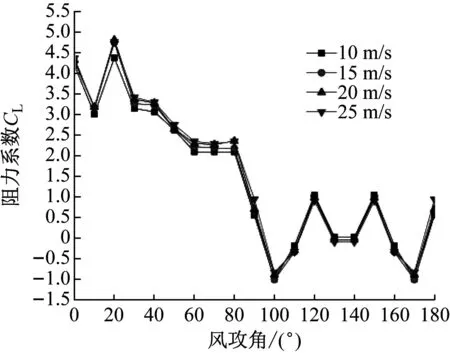
(b) 升力系數

3.3.1 冰棱長度對氣動力的影響

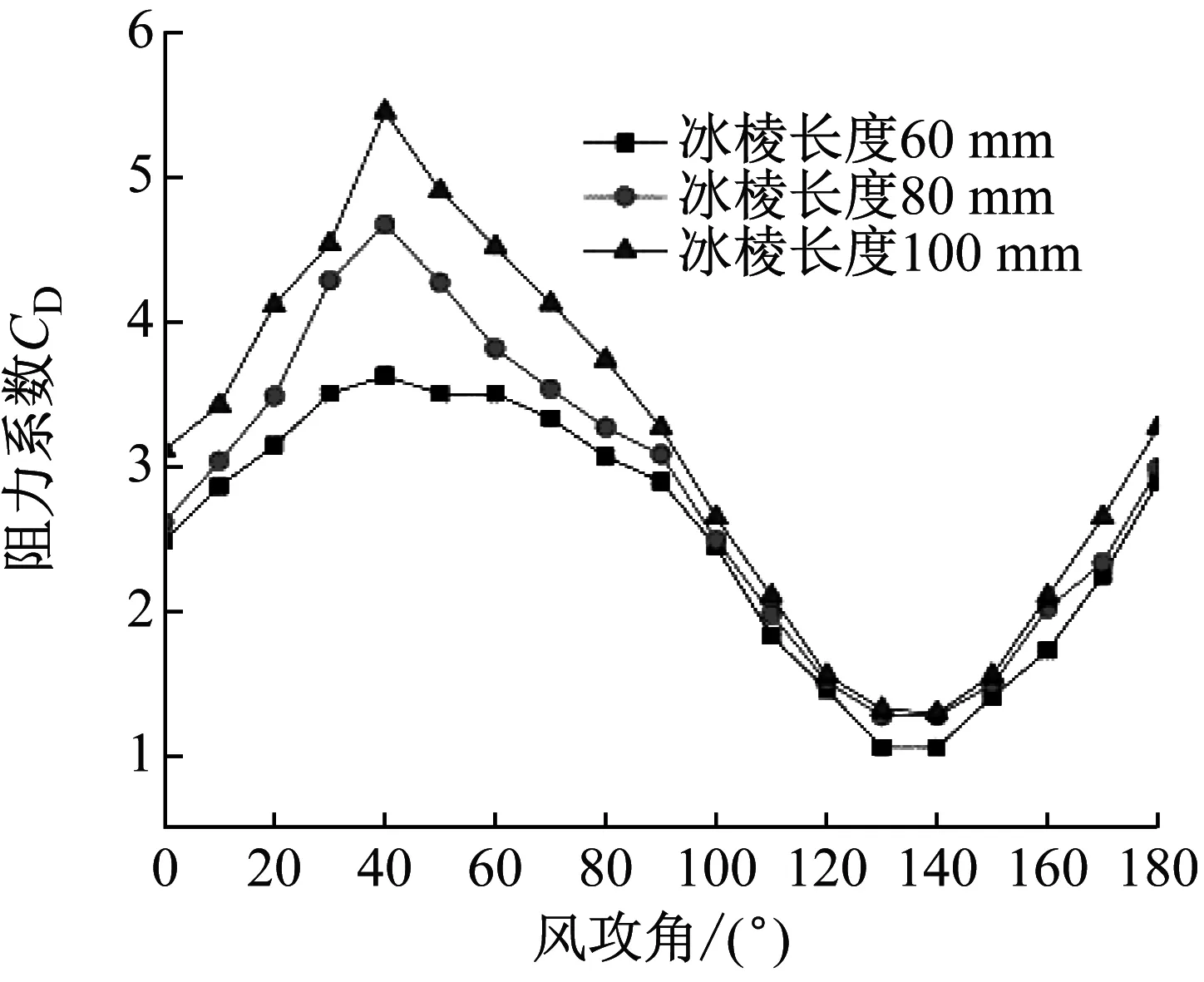
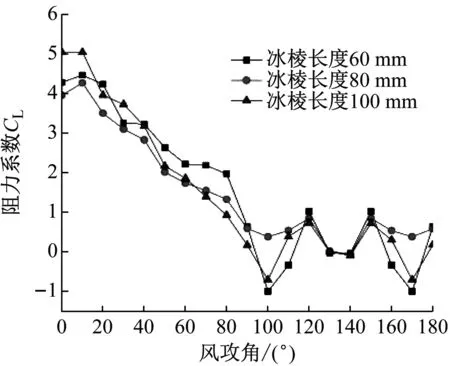
選取冰棱長度分別為60 mm、80 mm、100 mm，風速為15 m/s時進行分析，圖10為不同冰棱長度下覆冰導線氣動力參數。

由圖10可知，隨著冰棱長度增加，在任意風攻角下覆冰導線阻力系數均增大。冰棱長度增加沒有改變阻力系數最大值和最小值出現風攻角，在風攻角為40°時取最大值，在風攻角為130°～140°區間取最小值。升力系數受冰棱長度影響并不像阻力系數那樣明顯，整體趨勢表現為先減小再增加。由于不同冰棱長度風場相互影響存在差異，導致升力系數變化復雜。在風攻角為10°時，取得最大值且冰棱長度100 mm值最大；在風攻角為100°和170°時，取得最小值且冰棱長度60 mm值最小。

3.3.2 冰棱間距對氣動力的影響

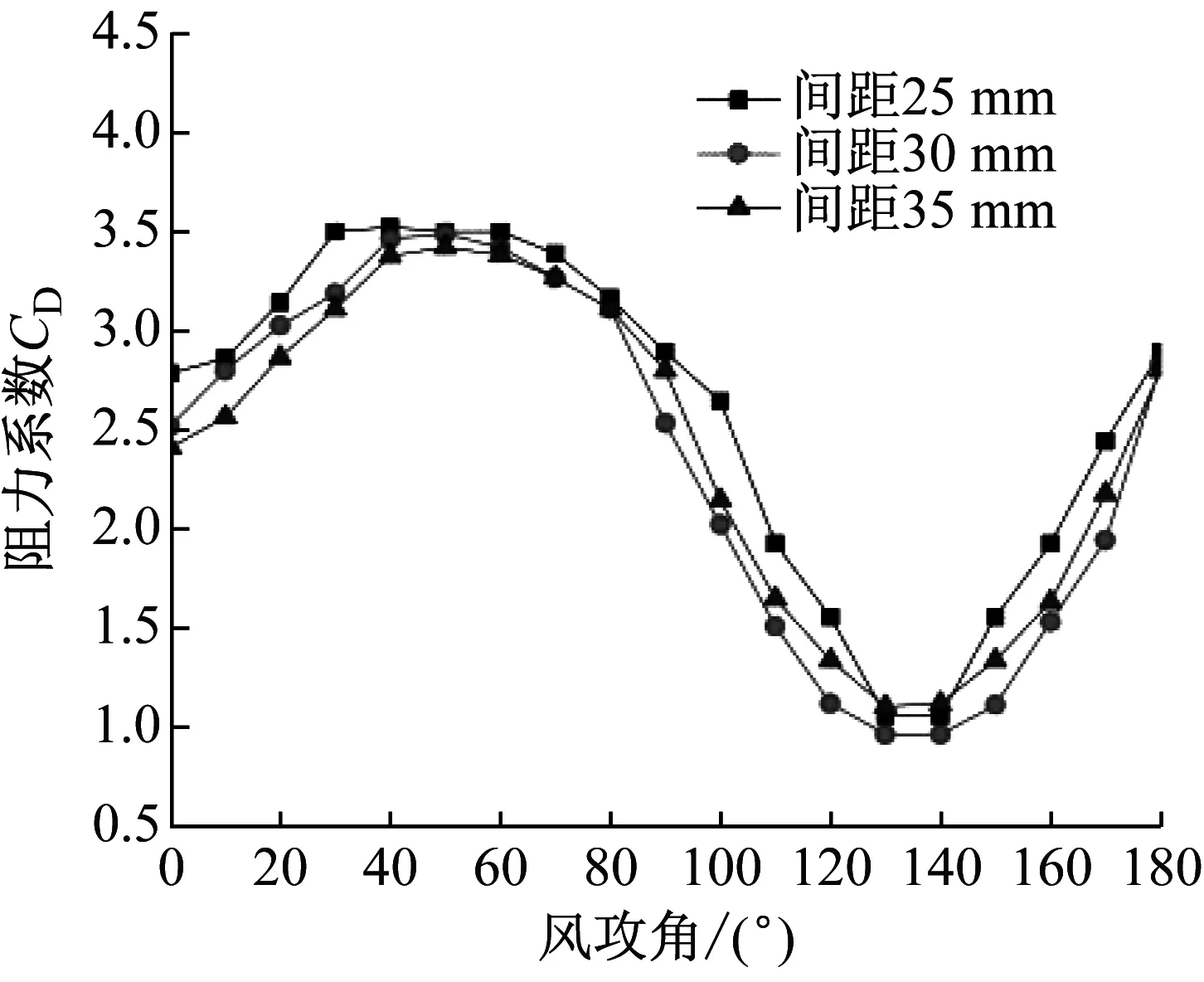
考慮冰棱間距對覆冰導線氣動力的影響，選取冰棱間距分別為25 mm、30 mm、35 mm，風速為15 m/s時進行分析，圖11為不同冰棱間距下覆冰導線氣動力參數。

由圖11可知，阻力系數在風攻角40°時，取得最大值且冰棱間距25 mm值最大；在風攻角130°～140°區間時，取得最小值且冰棱間距30 mm值最小。升力系數受相鄰冰棱間距影響較大，隨著攻角增加，升力系數先減小再增加。相鄰冰棱間距為25 mm時，隨著攻角增加，升力系數變化幅度最大。

(a) 阻力系數

(b) 升力系數

(a) 阻力系數

(b) 升力系數

3.4 全攻角下三維冰棱覆冰導線馳振力系數

通過式(5)計算可得到平均升力系數隨風攻角變化曲線的斜率值與平均阻力系數的和值，即馳振力系數。對于一個特定風攻角而言，?CL/?α可能取CL-α曲線的左側曲線斜率或者右側曲線斜率。兩種情況下計算馳振力系數隨風攻角變化的數值見圖12，當任意風攻角處左側馳振力系數和右側馳振力系數均小于零(<0)時，認為冰棱覆冰導線出現馳振舞動。

圖12 三維冰棱覆冰導線馳振力系數(風速：15 m/s，間距：25 mm，棱長：60 mm)

由圖12可知，當風攻角為50°、90°、160°時，通過式(5)計算得到的馳振力系數均為負值，表明在這些風攻角下冰棱覆冰導線處于非穩定狀態，極易發生覆冰馳振舞動。

4 結 論

(1) 三維五冰棱覆冰導線迎風側最大壓力分布呈現周期性變化，主要分布在覆冰圓柱下半部分和冰棱上半部分；分布面積由大及小再由小及大，周期時間為1.25 s。說明覆冰導線上冰棱存在對覆冰導線流體繞流特性有極大的影響。

(2) 冰棱覆冰導線在風攻角50°～60°區間取得阻力系數最大值，在風攻角130°～140°區間取得阻力系數最小值；升力系數出現最大值和最小值風攻角分別為20°和100°、170°，且隨著風速增加，升力系數最大值和最小值均有所增加。

(3) 隨著冰棱長度增加，覆冰導線阻力系數最大值由3.42增長到5.47，升力系數在風攻角10°時，取得最大值且冰棱長度100 mm最大；在風攻角100°和170°時，取得最小值且冰棱長度60 mm最小。

(4) 根據Den Hartong覆冰舞動理論計算，三維五冰棱覆冰導線在50°、90°、160°風攻角時對應風攻角計算得左側馳振力系數和右側馳振力系數均小于零(<0)，表明冰棱覆冰導線處于非穩定狀態，冰棱覆冰導線出現馳振舞動概率極大。