大型風力發電機組控制技術研究

張美倫，朱明澤，張 瑾，趙劍鋒，張 睿

(1.國網黑龍江省電力有限公司電力科學研究院，哈爾濱 150030; 2.哈爾濱電氣國際工程有限責任公司，哈爾濱 150028;3.國網黑龍江省電力有限公司，哈爾濱150090; 4.大連土城子風電有限公司,遼寧 瓦房店116327；)

0 引 言

隨著風電機組單機容量與風電規模的不斷提高，風電滲透率逐漸增高，現代風電機組的運行控制不但注意到風電場正常狀態下的遙測、監控，而且開始轉向風電機組與電網系統相互協調一體化的運行控制研究[1]，如風電機組有功功率控制、無功功率控制、低電壓穿越以及對稱和不對稱故障下的安全運行(故障穿越)問題等。因此，根據調度指令進行單機有功、無功調節，實現大型風電機組的自適應調節與并網，從電網層面靈活響應對風電機群有功、無功控制和優化調度的要求具有重大意義。

目前，國內對大型風力發電控制技術的研究只停留在傳統控制技術上面，這種方法采用了線性控制方法，是以線性模型為基礎，但是對于急劇變化的風速調整具有相對滯后的缺點[2]。此外，采用基于某一工作點的線性模型方法只能夠保證在線性化工作點附近的控制效果，因此并不適用于運行范圍廣、不確定性強、隨機擾動大、具有嚴重非線性特征的風力發電系統[3]。

針對上述問題，提出將現代控制方法(包括人工智能控制、最優控制、自適應控制、魯棒控制、切換控制等)引入大型風電機組的控制中，對大型風力發電機組的動態進行建模，研究風電系統的控制方式和設計有效的控制律，使風力發電機組對參數攝動和負荷擾動具有強魯棒性，保證風電機組安全高效運行。

1 系統關鍵控制技術研究

采用快速最佳葉尖速比控制實現柔性變槳，在最佳葉尖速比控制的基礎上，引入自適應分段控制技術，設計大型風電機組的智能化柔性變槳算法和柔性偏航算法，實現大型風電機組有功、無功的分段線性控制。具體通過以下各個小節描述的優化控制技術，保證了系統實現柔性變槳、變速與偏航，以及風電機組的整體智能化控制，降低對整機各個部分的沖擊，實現低噪聲運行。

1.1 最佳葉尖速比控制

葉尖速比是葉片葉尖線速度與風速的比值[4]，最佳葉尖速比法是在不同風速下，通過機械側轉換器控制電動機的轉子速度，使得風力渦輪機可以在最佳葉尖速比的狀態下運行，由此獲得風電功率最大值[5]。最佳葉尖速比控制方法的原理如圖1所示。根據當前測得的風速v，經查表可知該風速下的最佳葉尖速比，并將該值作為參考值λref。測量當前葉片轉速ω，通過公式λ=ωR/v計算獲得葉尖速比，與參考值進行比較后，進行PI調整，將調節器輸出信號發送至風機控制系統，由此可實現風機最佳葉尖速比控制。

圖1 葉尖速比控制圖Fig.1 Diagram of tip speed ratio control

1.2 完全獨立變槳控制

完全獨立變槳控制的目標是實現全掃風面變槳，減少葉片應力周期性沖擊，穩定整機載荷和延長葉片壽命。在實現完全獨立變槳控制的基礎上，才能夠實現單個葉片的自適應控制[6]。

獨立變槳距控制系統如圖2所示，獨立變槳控制器的功能主要是控制系統的位置、轉矩、速度等參數，獨立變槳伺服驅動器具有定位和同步調整的功能，槳距角位置經內齒傳感器檢測，與伺服電機的轉子位置進行同步，槳距角可以用作反饋狀態變量，以實現伺服電機的同步控制，由此達到獨立變槳控制。

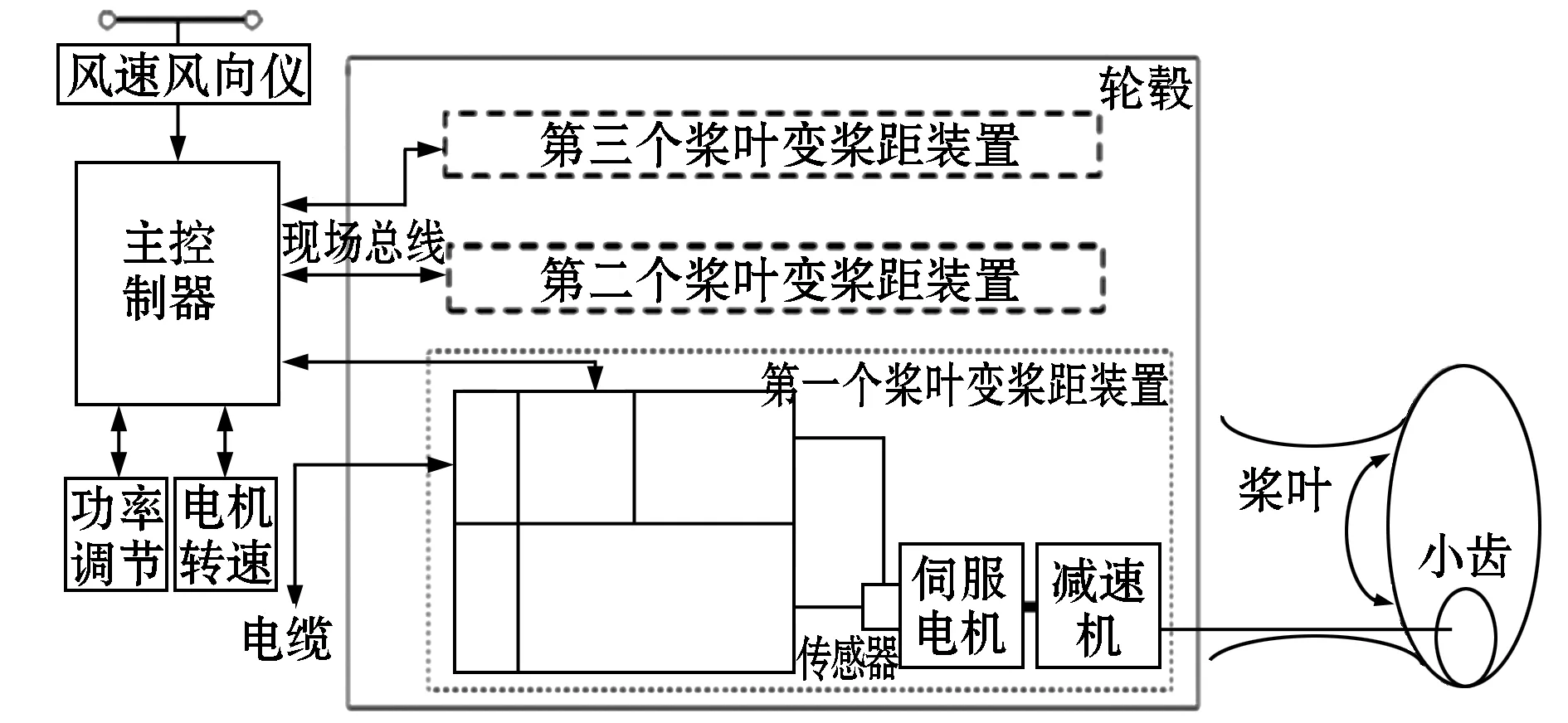
圖2 獨立變槳距控制系統圖Fig.2 Diagram of independent pitch control system

1.3 葉片自適應控制

大型風電機組是一個復雜的非線性系統，難以獲得系統的所有控制狀態，但控制系統的輸入和輸出量是確定的，因此可根據被控對象的狀態空間建立模型參考自適應控制系統[6]。

建立3個葉片運行一周的狀態空間模型，將3個葉片的控制目標設計為同一個參考模型，利用李雅普諾夫函數直接法設計3個葉片的模型參考自適應控制率，使得3個葉片在運行一周的過程中對主軸的應力盡量保持一致，變槳系統對于塔筒效應和葉片制造過程中的離散性誤差有著明顯的適應性，控制性能良好，能夠有效保證系統的穩定性。

完全獨立變槳控制與葉片的自適應控制相結合，實現了風機的自適應分段控制，在低風速(啟動風速至5 m風速)、中段風速(5 m至額定風速)、高風速(額定風速以上)時，分別設置了3個不同的參考模型，使得系統在這3段風速之下可以很好地實現最大功率跟蹤控制的同時，3個葉片保持平衡，對主軸沖擊最小，具體結構圖如圖3所示。

1.4 柔性偏航

偏航控制的主要功能之一是能夠使風輪跟蹤變化穩定的風向，通過控制風輪的迎風面與風向始終保持垂直以實現風能的最大捕獲[7]。當風向發生變化時，由風速風向儀測得風向變化，由偏航控制器控制偏航驅動裝置中的3～5臺偏航電機旋轉，偏航電機通過減速齒輪箱帶動小齒輪旋轉，使機艙往風速變化的方向同步運轉。

原有的偏航電機(3～5臺)在運行過程中出現不能完全同步現象，即偏航過程中某個偏航電機驅動的小齒輪與另一個偏航電機驅動的小齒輪無法完全同步帶動大齒圈，導致互相拉扯發出低頻噪音的現象。為此，采用主從力矩變頻驅動偏航策略，使得多個偏航電機能夠完全同步運行。采用主從力矩變頻驅動的柔性偏航技術，除了降低噪音外，還能夠延長齒圈和電機的使用壽命。

圖3 獨立變槳線性時變參數系統自適應控制結構圖Fig.3 Adaptive control structure diagram of independent pitch linear time-varying parameter system

1.5 低電壓穿越

當電網電壓下降時，電網側變流器會出現過流現象，如果采取限制電流的措施，直流母線就會產生過電壓；如果沒有采取有效的保護措施，將無法保證風機的安全穩定運行[8]。因此，需根據實際的風電狀態、持續時間、電壓跌落等情況，確定機組采用的保護策略，以滿足風電并網時的低壓穿越要求。

在風速低、系統壓降小的情況下，適當提高系統側變流器電源裝置的過電流水平和直流側電容器的抗電壓水平，可以實現低電壓穿越。但如果風機在額定狀態下運行時，電網電壓大幅下降，且持續時間較長， 變流器的成本會大幅增加， 因此這種保護措施并不適用。

在風速高且電網電壓大幅下降的情況下，在發電機直流側和輸出端增設Crowbar電路或輔助變流裝置，主要作用是限制故障時轉子側的過電流和過電壓，可以消耗、轉移或存儲過剩的能量，使得風機在電網發生故障時也能夠實現低電壓穿越，過程如圖4所示。

在圖4中保護點1位置增加Crowbar電路，在電網電壓跌落的情況下，該電路能夠平衡輸入與輸出間的能量差，避免了變流器過電流和直流母線過電壓對風機產生的沖擊。當電網電壓恢復正常時，則迅速切斷Crowbar電路，使風機恢復正常發電狀態運轉。

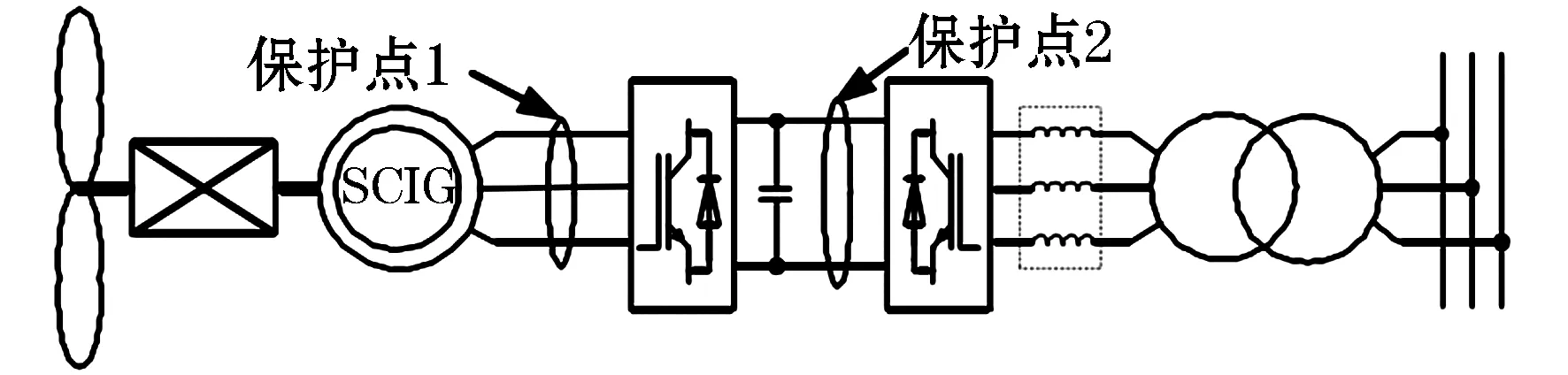
圖4 電機直流側和輸出端增設Crowbar電路Fig.4 Crowbar circuit is added to the motor output terminal and DC terminal

2 控制策略研究

結合傳統矢量控制的基本思想，引入自抗擾控制(adaptive disturbance rejection control,ADRC)、神經網絡，設計一種抗干擾能力較強控制算法，控制器內環基于BP神經網絡實現轉子d、q軸電流控制，控制器外環基于自抗擾控制的有功、無功控制，目標是使得控制系統對內、外擾動具有較強的魯棒性。根據傳統控制模式的不足，結合自抗擾控制的優點和BP神經網絡的優點，采用基于神經網絡的電流內環控制和基于自抗擾控制的功率外環控制。系統整體的控制拓撲圖如圖5所示。

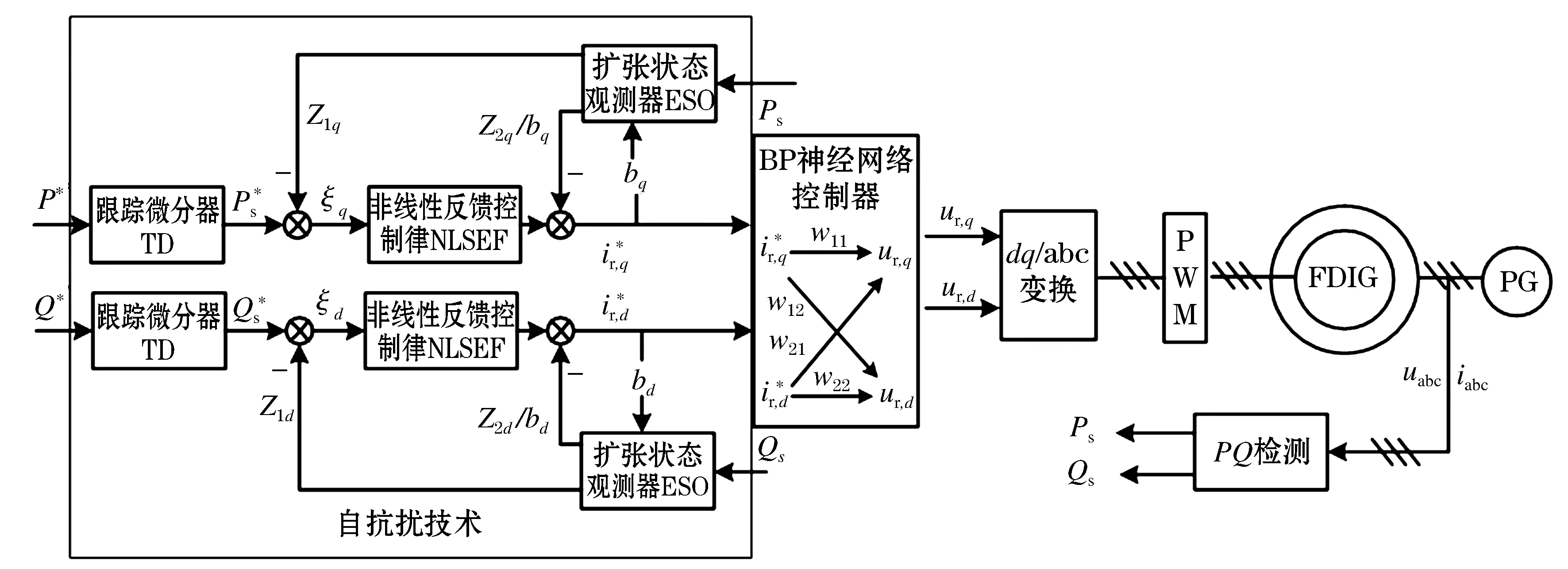
圖5 基于自抗擾神經網絡控制技術原理圖Fig.5 Schematic diagram of control technology based on adaptive disturbance rejection and neural network

2.1 自抗擾控制系統設計

自抗擾控制系統的設計包括三個部分：跟蹤微分器TD(tracking-differentiator)、擴張狀態觀測器ESO(extended state observer)和非線性反饋控制律NLSEF(nonlinear states error feedback)。各個部分相關的參數采用“分離性原理”獨自整定。

1)跟蹤微分器TD設計

對有功功率和無功功率的跟蹤采用一階微分器。微分器的模型如下：

(1)

(2)

2)擴張狀態觀測器ESO設計

以檢測的雙饋電機定子側有功功率Ps和無功功率Qs為量測輸入分別構造擴張狀態觀測器，如式(3)所示。

(3)

式中：x代表d或q；y表示P或Q(當x為d時，y為Q；當x為q時，y為P)；Z1x為定子有功功率和無功功率的實際跟蹤值；Z2x為擾動量的估計值；仿真時具體的相關參數取值β1x為300，β2x為400，α1x為0.8，δ為0.005，bx為500。

3)非線性反饋控制律NLSEF的設計

(4)

式中：βq的值為400；βd的值為350；αq和αd都為0.7；δ為0.005。

2.2 BP神經網絡控制系統設計

BP神經網絡控制器通過在線調節權值w11、w12、w21、w22使有功功率和無功功率的目標函數逐漸達到最小值，從而實現發電機有功功率和無功功率的獨立跟蹤控制，BP神經網絡的目標函數為

(5)

根據梯度法調節權值，得到權值變換量，具體如下：

(6)

式中：η為學習速率，取值為0.1。由式(6)可以對權值不斷更新，從而搜尋到一組最優權值使目標函數為最小值。

3 仿真結果與分析

為了驗證ADRC-BP控制技術的性能，在Matlab 2012b/Simulink平臺上對雙饋發電機分別采用空間矢量控制方法和基于ADRC-BP控制方法進行仿真。仿真所用雙饋電機的主要參數為：定子額定電壓690 V，額定功率2.0 MW，定子電阻為3.74 Ω，定子漏感為0.31 H，轉子電阻為3.2 Ω，轉子漏感0.31 H，定轉子互感1.2 H，極對數為2。系統額定風速為11 m/s，輸入風機的風速為9 m/s(此時對應的視在功率為1 MW)。

仿真驗證包括三個部分：當電網對稱，給定功率發生變化時，比較兩種控制算法的性能；當雙饋電機參數發生變化，給定功率不變，比較兩種控制算法的性能；當電網電壓出現波動，給定功率不變時，比較兩種控制算法的性能。

1)當有功功率和無功功率參考值變化時

保持輸入風速不變，并設定有功功率參考值為600 kW，無功功率的參考值為800 kvar；在仿真時間為0.5 s時，將有功功率和無功功率的值分別設定為800 kW、600 kvar，采用空間矢量控制算法和ADRC-BP算法得到的仿真結果如圖6所示。

2)當電機參數發生改變時

保持輸入風速不變，并設定有功功率參考值為800 kW，無功功率的參考值為600 kvar；在仿真時間為0.5 s時，雙饋電機的定子側電阻變為原來的1.5倍，采用空間矢量控制算法和ADRC-BP算法得到的仿真結果如圖7所示。

圖6 功率參考值變化時電氣量仿真波形對比圖Fig.6 Comparison diagram of electrical quantity simulation waveform when power reference value change

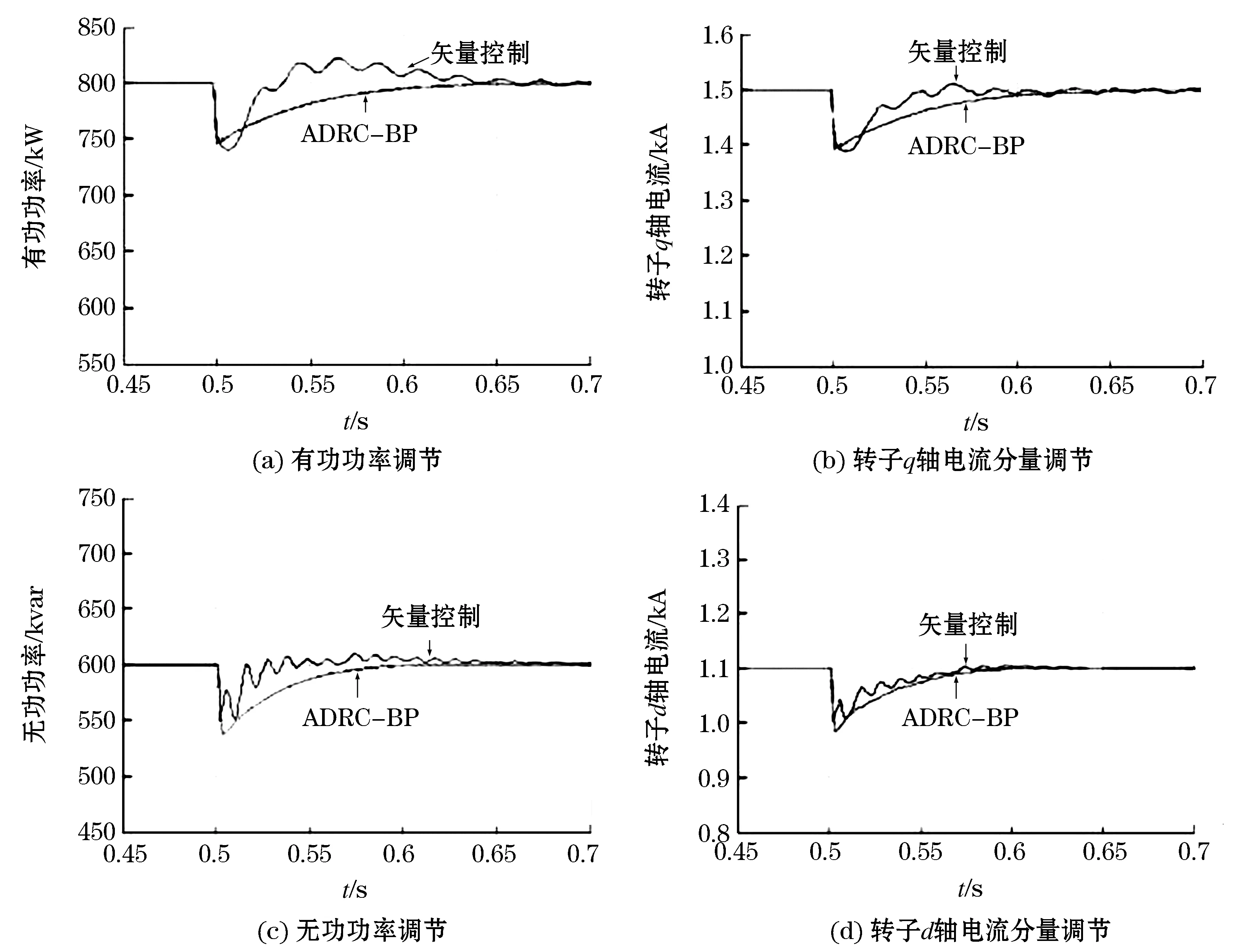
圖7 電機參數變化時電氣量仿真波形對比圖Fig.7 Comparison diagram of electrical quantity simulation waveform when motor parameters change

3)當電網電壓波動時

保持輸入風速為9 m/s不變，并設定有功功率參考值為800 kW，無功功率的參考值為600 kvar；在仿真時間為0.5 s時，電網電壓變為原來的0.9倍，且在1s時變為原來值，采用空間矢量控制算法和ADRC-BP算法得到的仿真結果如圖8所示。

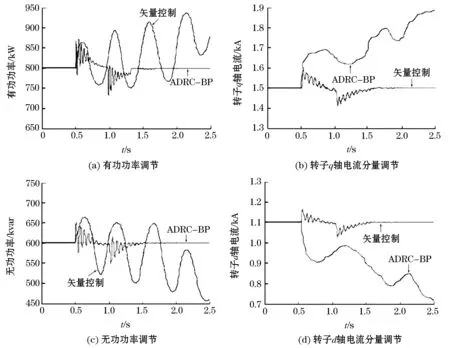
圖8 電網電壓波動時電氣量仿真波形對比圖Fig.8 Comparison diagram of electrical quantity simulation waveform when grid voltage fluctuates

如圖6～8所示，當參考功率變化時，ADRC-BP算法比矢量控制算法具有更快的跟蹤速度，且波動量小；當電機參數改變時，ADRC-BP算法經過短時間平緩地過渡到穩態，且穩態無誤差，而矢量控制的波動性比較大，且達到穩態所需時間較長；當電網電壓波動時，ADRC-BP算法能夠經過調整最終達到穩態，而矢量控制最終導致發散。由此可知，當電網處于不同運行狀態時，采用ADRC-BP控制方法提升了系統的穩定精度，使系統具有較好的穩態性能和較強的魯棒性。

4 結 語

該文結合風電機群能量管理與優化調度對大型風電機組的技術需求，在模型仿真和控制策略驗證的基礎上，引入自適應分段控制技術，并設計了自抗擾控制系統，設計了智能化柔性變槳算法和柔性偏航算法，實現了風電機組有功無功的分段線性控制，并具備低電壓穿越能力，降低機組運行噪聲，延長機組壽命，提升了大型風電機組的自適應控制能力。