淺談教材的創造性使用

汪昭潮

教師要創造性地使用教材，用教材教，而非教教材。筆者以人教版四年級下冊第三單元《乘法分配律》的教學為例，淺談如何創造性地使用教材。

一、置換情境，激發學習興趣

興趣是最好的老師。當教材提供的情境離學生較遠時，教師可以置換情境，激發學生的學習興趣。

《乘法分配律》教學中，教材選取的是植樹情境：參加植樹活動的同學一共有25個小組，每組4人負責挖坑種樹，2人負責抬水澆樹，要求一共有多少人。由于很多學生沒有參加集體植樹活動的生活經驗，很難激起他們的學習興趣。因此，筆者根據執教班級學生的特點，嘗試更換學生更加熟悉的場景。教學片段如下：

師：學校每個月都要收取午餐費，每個學生每餐是12元，五（5）班有男生24人，女生20人。對此你能提出什么數學問題？

生1：五（5）班一天要交多少餐費？

生2：五（5）班男生一天交多少餐費？

生3：五（5）班女生一天交多少餐費？

生4：五（5）班一個月要交多少餐費？

……

師：大家提的問題都很有意義，我們這節課主要解決第一個問題：五（5）班一天要交多少餐費？哪位同學愿意上臺來交流你的算法？

生5：我們可以先算出全班男生一天的餐費，即12×24=288（元），再算出全班女生一天的餐費，即12×20=240（元），然后把這兩個結果相加，即288+240=528（元）。

生6：我和他的方法一樣，用的綜合算式：12×24+12×20=528（元）。

生7：我是先算出全班總人數，24+20=44（人），因為每人餐費12元，所以全班總共餐費是12×44=528（元）。綜合算式是12×（24+20）=528（元）。

師：這兩種不同的方法都能正確求出全班的總費用，說明這兩個綜合式有什么關系？

生（齊）：相等。

師：關于這兩個相等的綜合算式，同學們有什么要提醒別人要注意的嗎？

生8：12×（24+20）≠12×24+20，不能直接把括號拿掉，等號右邊應當是兩個乘法算式，里面都要有12。

生9：我補充，因為12×24表示男生一天的餐費，而20是女生人數，男生一天的餐費和女生人數相加沒有意義。

“收餐費”這一和學生生活息息相關的情境，能激活學生的生活經驗，激發學生的學習興趣，讓學生認真參與到教學活動中。在教師的引導下，學生把目光聚焦到提出的第一個問題，興致勃勃地去解決它。此外，學生還能結合這一具體事例，解釋為什么“12×（24+20）≠12×24+20”，從而在理解的基礎上認識了乘法分配律的基本特征，為正確抽象出乘法分配律模型奠定基礎。

二、增添素材，豐富認知體驗

數學是抽象的學科，抽象是數學學習的重要目標。僅僅使用上述一個例子必然會造成學生感知素材單一、體驗匱乏，達不到抽象出乘法分配律模型的要求。這個時候，教師需要適當增加一些素材，讓學生在多樣化的情境中，充分積累經驗，豐富認知體驗，加深對乘法分配律特征的認識。

首先，教師可以創造性地使用課本例題，讓學生用兩種不同的方法求參加植樹的人數;然后，創編一道求長方形植樹地周長的題（如下圖），讓學生結合長方形實物圖，說明兩種求周長的方法分別是（37+13）×2和37×2+13×2;最后，讓學生根據上述算式的特征，舉出一些類似的例子，讓學生對乘法分配律的特征有足夠清晰的認識。有了上述充足的認知體驗后，再讓學生嘗試抽象出乘法分配律的字母公式“（a+b）×c=a×c+b×c”，就水到渠成了。

三、多維思考，探尋內在道理

在抽象出數學模型后，教師可以讓學生多維度探尋內在道理，加深對知識的理解。教師可以通過提出“怎樣理解a×（b+c）=a×b+a×c呢？”這個問題驅動學生的思維走向更深層次，去探尋知識的本質。

首先，學生已經有了上面例題的鋪墊，會從整數乘法的意義去解釋：a×（b+c）可以理解為（b+c）個a的和，a×b可以理解為b個a的和，a×c可以理解為c個a的和，因此（b+c）個a的和就等于b個a的和加c個a的和。

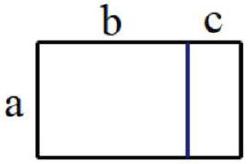
其次，乘積與長方形的面積計算可以密切結合起來，教師可以構造出求長方形面積的直觀圖形來解釋乘法分配律（如下圖）。

求大長方形的面積有兩種思路。一是分別求出兩個小長方形的面積，即左邊長方形的面積為a×b，右邊長方形的面積為a×c，再把兩者相加，所以整個大長方形的面積可以表示為：a×b+a×c。第二種思路是把上圖看作一個整體，長為（b+c），寬為a，所以大長方形的面積也可以表示為a×（b+c）。既然都是求長方形的面積，那么自然可以得到a×（b+c）=a×b+a×c。結合圖來看，乘法分配律可以這樣理解：乘法分配律的實質就是對大長方形面積求法的兩種不同方法，要么先求出每個小長方形的面積，再把二者相加，要么當作一個整體，先求出大長方形的長再直接求大長方形的面積。更簡單地說，就是大長方形的面積，可以先求部分再求和，也可以整體來算。

四、適度拓展，誘發頭腦風暴

數學課絕不僅僅是教學知識、技能，更重要的是數學承載著發展人的思維的功能。作為一名數學教師，要給學生提供良好的平臺，讓學生的思維得到充分發展。

在經過上述充分的挖掘后，教師還可以圍繞乘法分配律進行適度的拓展，放飛學生的思維，誘發一場頭腦風暴。比如a×（b-c），括號里是兩個數的差，應該等于什么？a×（b+c+d），括號內部推廣到三個數，又該等于什么？甚至還可以將括號內的數推廣到n個，即a×（b1+b2+…+bn）又等于什么？學生有了對上述知識的探索，推理能力、創新能力都會得到顯著提升。

（作者單位：武漢經濟技術開發區神龍小學）

責任編輯 張敏