強化問題邏輯 引領(lǐng)解題方向

鄭 良

(安徽省合肥市第四中學(xué) 230000)

解題過程就是實現(xiàn)從條件到結(jié)論的通達(dá).教學(xué)中發(fā)現(xiàn)部分學(xué)生弄不清條件與結(jié)論的邏輯關(guān)系，常常在解題過程中出現(xiàn)不等價變形而不自知等等.如何避免邏輯關(guān)系的顛倒，實現(xiàn)問題的等價轉(zhuǎn)化？學(xué)生們不僅要有堅實的基礎(chǔ)知識、熟練的基本技能，必要的解題經(jīng)驗，還要具備通過閱讀理解題意、結(jié)合問題制定解題方案、根據(jù)困難所在調(diào)整思維方式、反思比較中優(yōu)化方法的能力.下面給出四道例題并對其關(guān)鍵點進(jìn)行點評，以期能對大家有所幫助.

例1 四邊形邊框頂點分別為A、B、C、D，一螞蟻沿折線BCDA由點B向點A運動，螞蟻位置P與AB構(gòu)成△ABP的面積為S，老師在黑板上畫出S=f(x)的圖像如圖1所示，同學(xué)甲、乙、丙、丁分別做出如下判斷：

甲：邊框ABCD是平行四邊形；

乙：邊框ABCD是等腰梯形；

丙：當(dāng)螞蟻到AD中點時，△ABP的面積是10；

丁：路程x∈[10,14]時，S=f(x)=56-4x.

試問哪些同學(xué)的判斷是正確的？

解當(dāng)x∈[5,9]時，從圖1可知△ABP的面積不變，此時S△ABP=20，則四邊形ABCD中必有兩邊AB與CD平行，且CD=4，BC=5，DA=5.

如圖2所示，若ABCD是平行四邊形，則S△ABP的最大值只能為10，達(dá)不到20.所以乙、丙、丁的回答是正確的.

(1)試求函數(shù)f(x)的解析式；

(2)是否存在直線L與y=f(x)的圖像只交于點P,Q兩點，并且使得P,Q的中點坐標(biāo)為(1,0)？若存在，求出直線L的方程；若不存在，請說明理由.

解(1)由f(x)是奇函數(shù)，易知c=0；

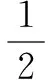
因此，直線L與函數(shù)f(x)的圖像共有三個交點，與“只交于兩點”矛盾.所以滿足條件的直線不存在.

例3 對于函數(shù)f(x)(x∈D)，若同時滿足以下條件：①f(x)在D上單調(diào)遞增或單調(diào)遞減；②存在區(qū)間[a,b]?D，使f(x)在[a,b]上的值域是[a,b].那么，我們把函數(shù)f(x)(x∈D)叫做閉函數(shù).

(1)求閉函數(shù)y=-x3符合條件的區(qū)間[a,b]；

(2)判斷函數(shù)y=2x-lgx是不是閉函數(shù)？若是，說明理由，并找出區(qū)間[a,b]；若不是，說明理由；

例4 已知動圓過定點P(1,0)，且與定直線L∶x=-1相切，點C在L上.

(1)求動圓圓心的軌跡M的方程；

(ⅰ)問：△ABC能否為正三角形？若能，求點C的坐標(biāo)，若不能，說明理由；

(ⅱ)當(dāng)△ABC為鈍角三角形時，求點C的縱坐標(biāo)的取值范圍.

解(1)由題意，曲線M是以點P為焦點，直線L為準(zhǔn)線的拋物線，所以曲線M的方程為y2=4x.

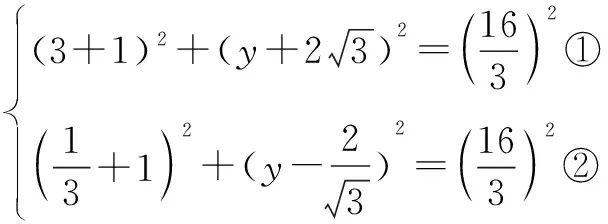
由①②組成的方程組無解，即直線L上不存在點C，使得△ABC為正三角形.

點評在第(2)(ⅰ)小題中，“|BC|=|AB|且|AC|=|AB|”是“△ABC為正三角形”的充要條件，但①-②得到(|BC|=|AC|所滿足)的方程③只是結(jié)論的必要條件，由等價變形可知①③或②③構(gòu)成的方程組為結(jié)論的充要條件.本題也可根據(jù)“△ABC為正三角形”由A,B求出點C的坐標(biāo)再驗證點C的橫坐標(biāo)是否為-1.在第(2)(ⅱ)小題中，首先要確保△ABC的存在性，由于以拋物線的焦點弦為直徑的圓與該拋物線的準(zhǔn)線相切，故∠ACB不可能為鈍角，解答中用余弦定理求解，需要解關(guān)于y的一元二次不等式.結(jié)合本題中點A,B是固定的，故可先根據(jù)CA⊥AB或CB⊥AB利用斜率關(guān)系找出臨界值，再結(jié)合圖形求解.