借力數學抽象 提升思維品質
王宏官

數學本質上是研究抽象的東西,主要包括:從數量與數量關系、圖形與圖形關系中抽象出數學概念及概念之間的關系,從事物的具體背景中抽象出一般規律和結構,用數學語言予以表征.
在學習過程中,如何發展自己的數學抽象素養,促思維品質的提升?
策略之一:挖掘定理公式推導過程中蘊含的思想方法,發展抽象思維品質
教材中正弦定理與余弦定理的推導方法中都用到了向量法和解析法,這兩種方法也正是我們解決三角形應用問題中常用的兩種思維角度.
敲黑板
教材中一些定理、性質和公式的推導過程往往隱藏了某一重要的數學思想或方法.我們不能只關注概念、法則和它們的應用,應多一份追求與思考,追根溯源,關注這些概念和法則產生過程、推導方法、滲透的數學思想與方法.
例1已知△ABC 的三邊長分別為AB=7,BC=5,CA=6,那么的值為________.
解析1(常規解法)利用余弦定理的推論與數量積的定義即可求解.
解析2(借助余弦定理的推導)注意到中向量與的形式,首尾相接.在△ABC中,平方得,代入解得
教材中有這樣一道習題:
在△ABC中,求 證:a2+b2+c2=2(bccosA+cacosB+abcosC).
再看這樣一道泰州聯考題:
在 △ABC中,a=3,b=4,c=6,則bccosA+cacosB+abcosC的值為________.
敲黑板
你的教材,多久沒碰啦?仔細閱讀過幾遍?
解題時如果我們想不到應用上題結論,而感到應用正弦、余弦定理無從下手時,應該跳出解三角形范疇,聯想到余弦定理與向量數量積的關系,得
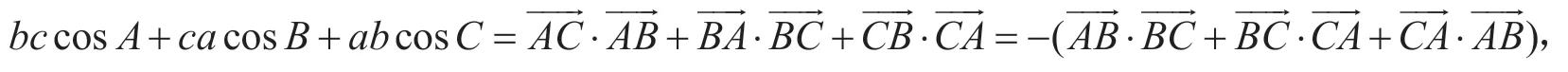
由上可以看出它們的轉化也正是基于余弦定理的推導過程,在具體情境中思考問題的背后是否隱藏了某些規律,抽象出其本質,達到多題歸一、多題一解之效.因此我們要善于從課本中概念、公式、定理的形成過程中發現規律、方法,發展抽象思維品質,提升數學抽象素養.
策略之二:積累從具體到抽象的活動經驗,提升數學抽象的思維品質
教材中有這樣一道例題:
直線y=x-2 與拋物線y2=2x相交于點A,B,求證:OA⊥OB.
面對這樣的問題,我們可以反思:能使OA⊥OB成立的關鍵條件是什么?
可以質疑:“拋物線y2=2x”中的“2”與“直線y=x-2”中的“2”是“巧合”?
嘗試將此系數進行一般化,抽象為一般:
直線y=x-2p與拋物線y2=2px(p>0) 相交于點A,B,OA⊥OB成立嗎?
發現此命題成立.
繼續反思:直線的斜率只能為“1”嗎?
嘗試將直線方程改為y=x2-2,推理發現OA與OB并不垂直.而將直線y=x-2改為直線y=2(x-2) 后,才會出現OA⊥OB.由此我們可再抽象為一般化的結論:
結論1直線y=k(x-2p) 與拋物線y2=2px(p>0) 相交于點A,B,有OA⊥OB.
結論2過定點(2p,0)的動直線和拋物線y2=2px(p>0) 相交于兩點A,B,O為原點,有OA⊥OB.
從上述命題探究過程中,可發現:
結論3若一直線與y2=2px(p>0) 相交于兩點A,B,O為原點,且OA⊥OB,則直線AB必過定點(2p,0).
由于O點是拋物線上一點,進一步一般化得到:
結論4若M(x0,y0)為y2=2px(p>0) 上一定點,過點M作拋物線的兩條互相垂直的弦MA,MB,則直線AB必過定點(x0+2p,-y0).
結論5M(x0,y0)為y2=2px(p>0) 上一定點,過點(x0+2p,-y0)的動直線與拋物線交于兩點A,B,則MA⊥MB.
至此,“直線、拋物線、頂點”這三個條件都已經進行了一般化(抽象)推廣.
如果再將“兩條互相垂直的弦”一般化為:兩條弦斜率之積為定值.進一步可得到:
結論6M(x0,y0)為y2=2px(p>0) 上一定點,AB為拋物線的動弦,若kMA kMB=λ,則直線AB過定點
還可以進一步抽象,將曲線改為圓、橢圓、雙曲線后,看看會得到什么樣的結論.
策略之三:熟悉常用的數學抽象方式,促成一般性思考問題的習慣
1.由特殊到一般的抽象方式
先看下面的問題:
例2 (2018·北京卷)設n為正整數,集合A={α|α=(t1,t2,…,tn),tk∈ {0,1},k=1,2,…,n}.對于集合A中的任意元素α=(x1,x2,…,xn)和β=(y1,y2,…,yn),記M(α,β)=[(x1+y1-|x1-y1|)+(x2+y2-|x2-y2|)+…+(xn+yn-|xn-yn|)].當n=3時,若α=(1,1,0),β=(0,1,1)……
分析當n=3 時,集合A={α|α=(t1,t2,t3),t1,t2,t3∈ {0,1}},α=(1,1,0),β=(0,1,1),
所以,M(α,α)=[(1+1-|1-1|)+(1+1-|1-1|)+(0+0-|0-0|)]=2,
M(α,β)=[(1+0-|1-0|)+(1+1-|1-1|)+(0+1-|0-1|)]=1.
通過對特殊情形“n=3”的探尋,我們可以進一步感知M(α,)β蘊含的信息,明確要研究M(α,)β的取值勢必要去掉絕對值的符號,自然需要討論xn和yn的大小關系,會尋找到解決問題的入口.
2.由整體到局部進行抽象方式
例3已知t為常數,函數y=|x2-2x-t|在區間[0,3]上的最大值為2,則t=______.
解析1(常規解法)通過二次函數的對稱軸和區間的關系,結合圖象進行分類討論.
解析2(換元法)將y=|x2-2x-t|中的x2-2x換元為u,那么原函數就轉化為y=|u-t|.先分析內層函數u=x2-2x.由x∈[0,3],得u∈[-1,3].
問題就等價轉化為:函數y=|u-t|在u∈[-1,3] 上的最大值為2,t=______.
借助絕對值的幾何意義,從而轉化為:u是區間[-13,]上的任意一點,且u與數軸上一點t的距離的最大值為2,求t的位置.很容易得到t=1.
數學抽象是學習數學的核心和靈魂,直接影響數學方法與思想的形成與構建.我們平時研究數學問題要學會由表及里,由淺入深,善于總結思辨,透過現象抓住本質,抽象歸納出解決問題的方法和思想,這樣才能構建出完整的數學結構體系,提升自己自己的思維能力.

