分析空間結構，發(fā)展直觀想象
——例談高三空間幾何體中垂直關系的復習

浙江安吉縣高級中學 (313300) 魏侹路

立體幾何教學的一項重要功能在于發(fā)展學生的直觀想象這一核心素養(yǎng).什么是直觀想象？課程標準中明確指出，它是指借助幾何直觀和空間想象感知事物的形態(tài)與變化，利用空間形式特別是圖形，理解和解決數學問題的素養(yǎng).它包括借助空間形式認識事物的位置關系、形態(tài)變化與運動規(guī)律[1].

空間位置關系中的重點和難點在于垂直關系的探索，空間角中線面角、二面角的尋找關鍵都在于垂直關系的尋找.學生很多時候不能找出所需的垂直關系，一方面是由于對垂直有關的判定定理和性質定理不熟悉，另一方面是因為對于幾何體的認識限于局部、缺少對圖形的分析形成整體的感知.所以，幫助學生形成對幾何體從整體到局部的認識，從具體到抽象的感知，加強學生對幾何體的圖形分析能力，對于高三學生的立體幾何復習十分重要.下面，筆者結合教學實際，談談對高三垂直關系復習的幾點想法.

一、借助模型，可以攻玉

分析幾何體的空間結構，應當先從分析其表面的平面圖形著手.面對復雜的幾何體時，有時可以將其分解，產生新的空間幾何形體，再正確分析其位置關系與數量關系，并對位置關系和數量關系進行論證與求解.因此，如果在日常學習中注意積累一些簡單幾何體中的垂直關系，將有助于我們探索復雜幾何體中的垂直關系.以下三種模型可以說是非常具有代表性的.

1.墻角模型

定義1 三條棱兩兩垂直的三棱錐.

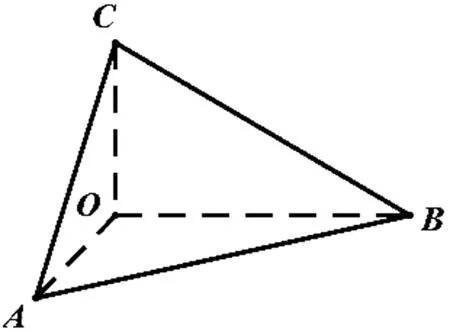
圖1

性質1 如圖1，三棱錐O-ABC中，OA,OB,OC兩兩垂直.則三棱錐各個面的垂線如下：顯然有OA⊥平面BOC，OB⊥平面AOC，OC⊥平面AOB，容易證明O在平面ABC內的投影為△ABC的垂心H，即OH⊥平面ABC.

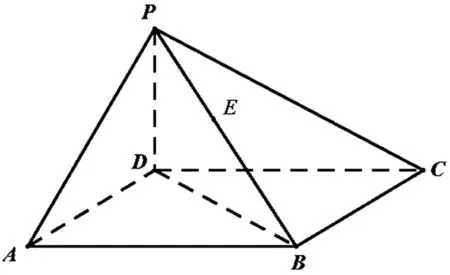
圖2

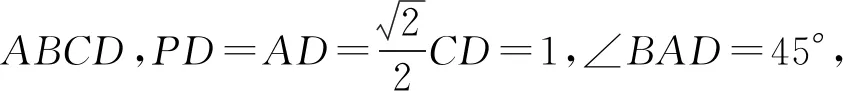
(Ⅰ)求證：DE⊥BC；

(Ⅱ)若平面PAB⊥平面DEC，求出此時PE的長度.

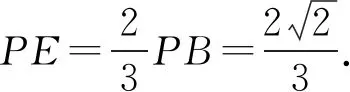
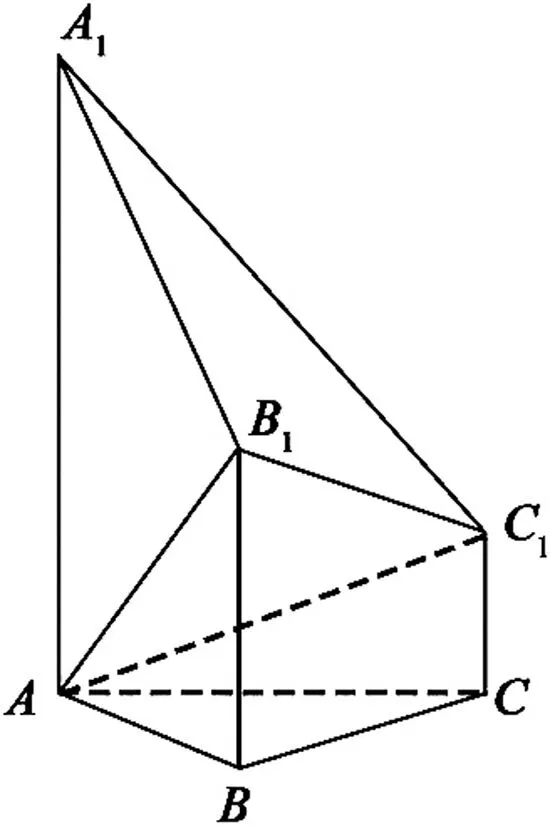
圖3

問題2如圖3，已知多面體ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2.

(Ⅰ)證明：AB1⊥平面A1B1C1；

(Ⅱ)求直線AC1與平面ABB1所成的角的正弦值.

圖4

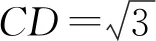
2.鱉臑模型

定義2 四個面都是直角三角形的三棱錐.

性質2 如圖5，三棱錐O-ABC中，OA,AB,BC兩兩垂直.則三棱錐各個面的垂線如下：OA⊥平面ABC，BC⊥平面AOB.作AE⊥OB,BD⊥AC，則AE⊥平面OBC，BD⊥平面OAC.

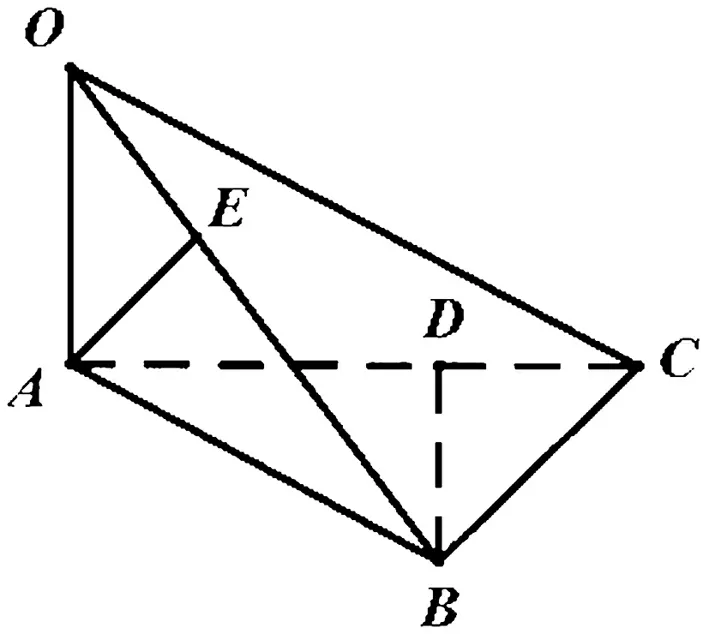
圖5

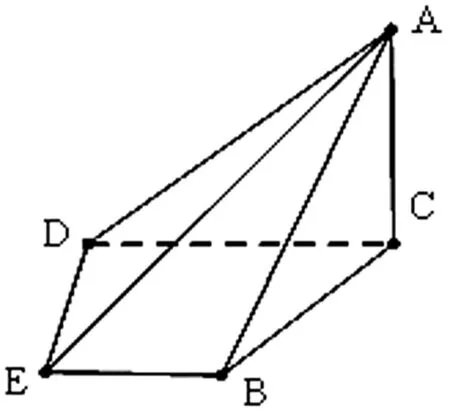
圖6

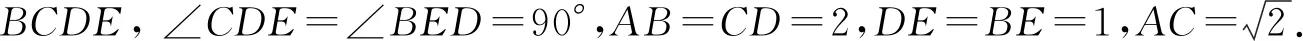
(Ⅰ)證明：EF平面△AEF；

(Ⅱ)求二面角△A′EF的大小.

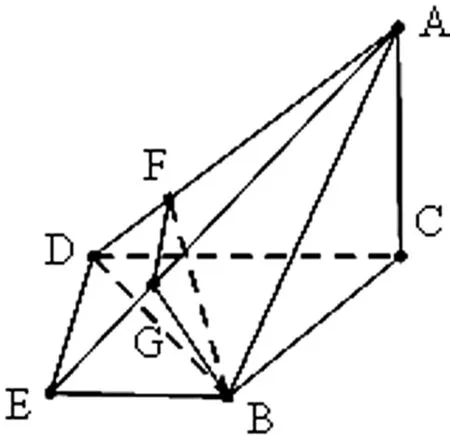
圖7

分析：此題是2014年浙江高考第20題.主要考慮第(Ⅱ)問，此題的常規(guī)思路如圖7，因為△AED,△ABD均為直角三角形，所以作BF⊥AD于點F，再作FG∥DE交AE于點G，連接BG，則∠BFG即為二面角△A′EF的平面角.雖然此法找出二面角的平面角并不困難，但是BG長度的計算較繁瑣.

當連接BD時我們發(fā)現，四棱錐A-BCDE被分割成了三棱錐A-BDE和三棱錐A-BDC，而且三棱錐A-BDC就是鱉臑模型.由(Ⅰ)可知面ADE⊥面ADC，故所求二面角即為二面角B-AD-C的余角.根據性質2，二面角B-AD-C在鱉臑體A-BDC中非常容易計算，只需要作BH⊥CD，再作HK⊥AD，連接BK，則∠BKH即為二面角B-AD-C的平面角.(計算過程略)

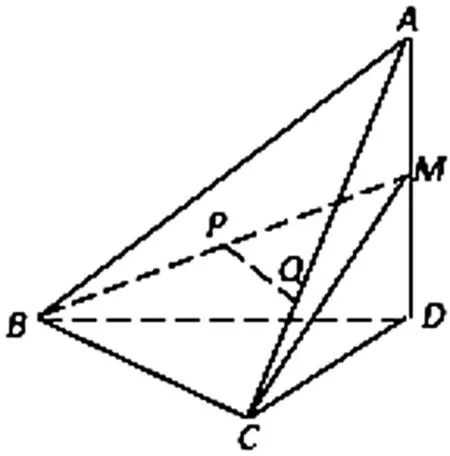
圖8

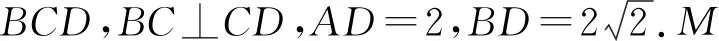
(Ⅰ)證明：PQ∥平面BCD；

(Ⅱ)若二面角C-BM-D的大小為60°，求∠BDC的大小.

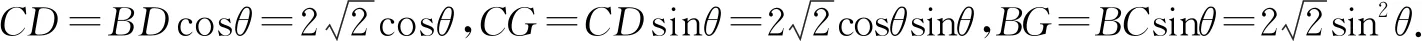
3.對稱模型

類似于平面幾何中軸對稱圖形的定義，推廣到三維空間中就可以得到“面對稱幾何體”.

定義3如果空間幾何體關于某個平面對稱，則稱這樣的幾何體為對稱幾何體，這個平面叫作該幾何體的對稱面.

下面以三棱錐為例進行相關的垂直分析.

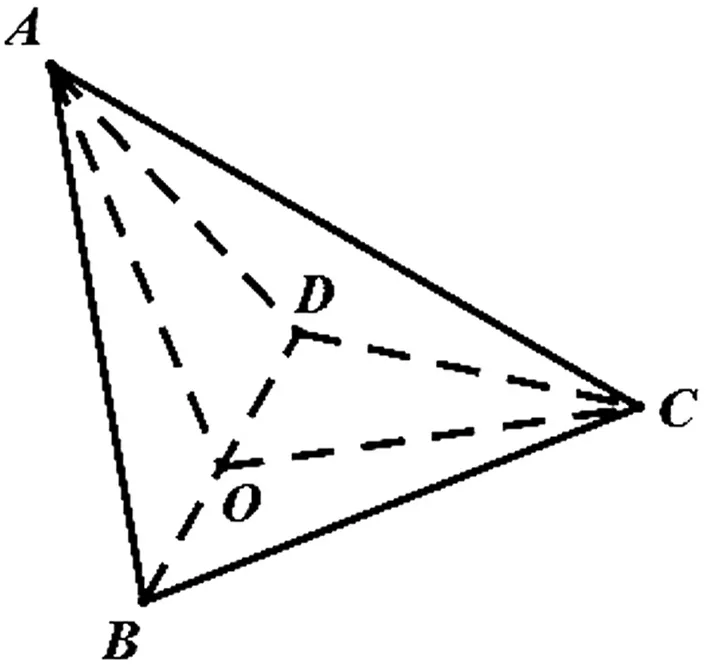
圖9

性質3如圖9，三棱錐A-BCD中，AB=AD,BC=BD.取BD中點O，則BD⊥平面AOC，進一步可得平面AOC⊥平面ABD，平面AOC⊥平面BCD.

一般的，如果一個多面體是對稱幾何體，那么它的對稱面會垂直于該多面體所有與之相交的表面.

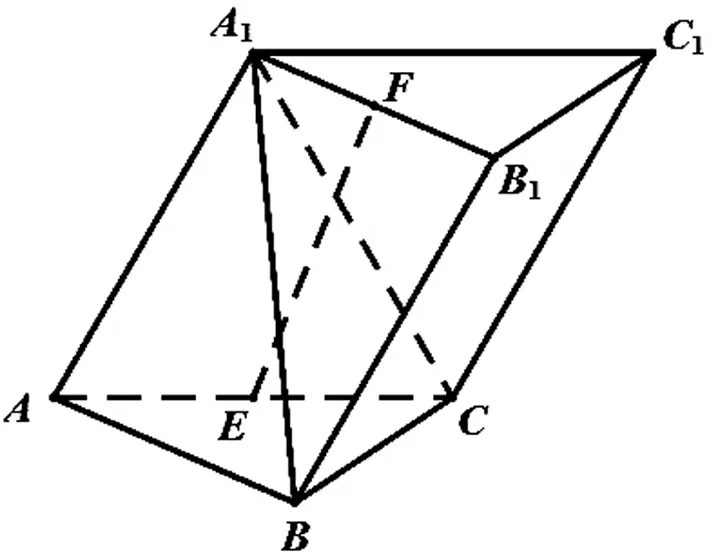
圖10

問題5如圖10，已知三棱柱ABC-A1B1C1，平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F，分別是AC，A1B1的中點.

(Ⅰ)證明：EF⊥BC；

(Ⅱ)求直線EF與平面A1BC所成角的余弦值.

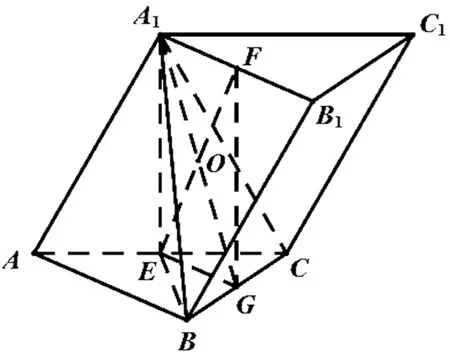
圖11

分析：此問題是2019年浙江高考第19題.因為平面A1ACC1⊥平面ABC，且A1A=A1C=AC，所以A1E⊥平面ABC.注意到E是Rt△ABC的外心，所以A1B=A1C，EB=EC，三棱錐A1-EBC是一個對稱幾何體.如圖11，取BC的中點G，連接EG，FG,A1EGF即為三棱錐A1-EBC的對稱面.根據性質3，我們知道平面A1EGF⊥平面A1BC.這個垂直關系的證明不僅解決了第(Ⅰ)問，而且為第(Ⅱ)問也指明了方向——點E在平面A1BC上的投影一定在兩個平面的交線A1G上，故∠EOG即為直線EF與平面A1BC所成角(或其補角).(計算過程略)

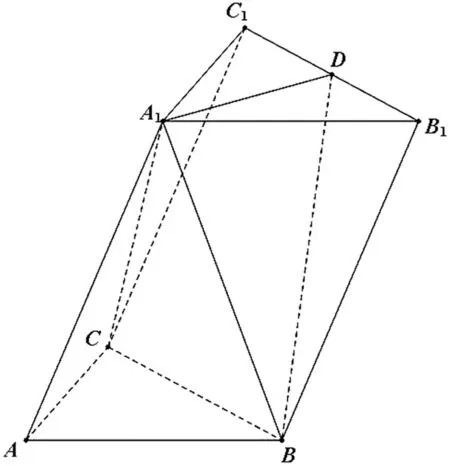
圖12

問題6如圖12，在三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=2,AA1=4，A1在底面ABC的射影為BC的中點，D為B1C1的中點.

(Ⅰ)證明：A1D⊥平面A1BC；

(Ⅱ)求二面角A1-BD-B1的平面角的余弦值.

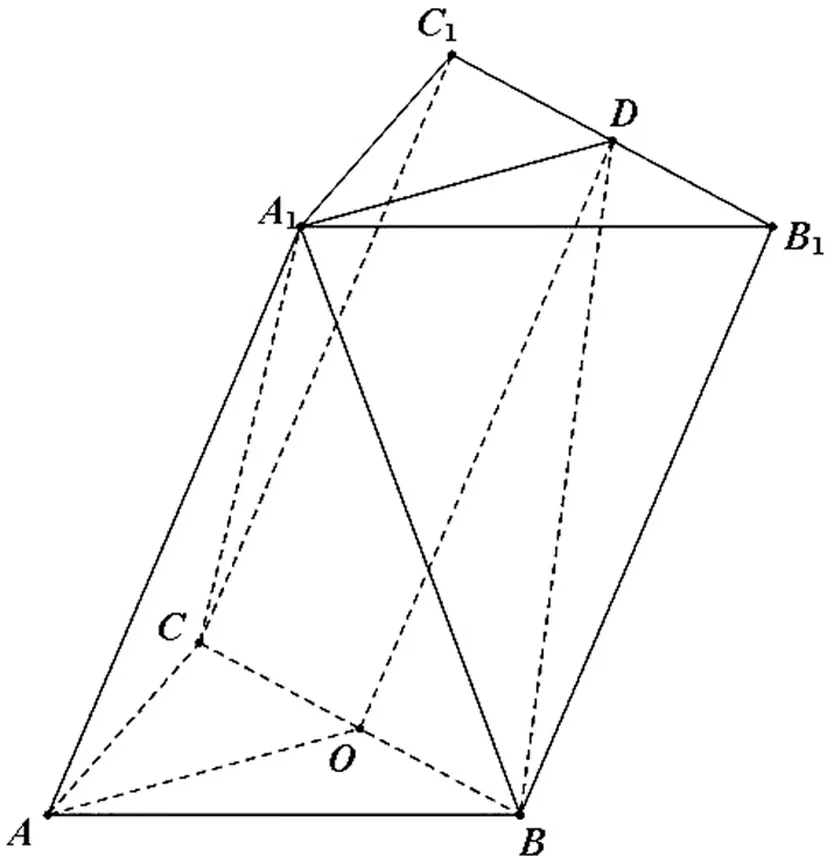
圖13

分析：此題是2015年浙江高考第17題，關鍵要分析出兩個垂直關系，一是面A1BC⊥面ABC，這點由“A1在底面ABC的射影為BC的中點”這一已知條件很容易得到，這個垂直關系是解決第(Ⅰ)問的關鍵.在第(Ⅱ)問中，如果能發(fā)現Rt△A1BD?Rt△B1BD，則二面角的平面角根據定義很快可以作得，這也是當年參考答案給出的解法.這里給出另外一種思路，由“A1在底面ABC的射影為BC的中點，AB=AC”這一已知條件可以知道這個斜三棱柱是一個對稱的幾何體.所以，根據性質3可知只要取BC的中點O，連接AO,OD，如圖13，則這個三棱柱的對稱面就是平面AODA1.一旦找到了面B1C1CB的垂面，接下來找二面角A1-BD-B1的平面角就是熟悉的問題了.

二、動態(tài)翻折，追根溯源

有時候一些幾何體可以看做是某個平面圖形翻折而成，那么在分析該幾何體的空間結構時，翻折的二面角大小往往是影響幾何體形態(tài)的關鍵因素.因此，以翻折所成的二面角為突破口，可以幫助我們從源頭上把握幾何體中的位置關系和數量關系.

問題7如圖14，已知等腰梯形ABCD中AB=4,BC=CD=DA=2，F為線段CD的中點，E，M為線段AB上的點，AE=EM=1.現將四邊形AEFD沿EF折起.

(Ⅰ)求證：AM∥平面BCD；

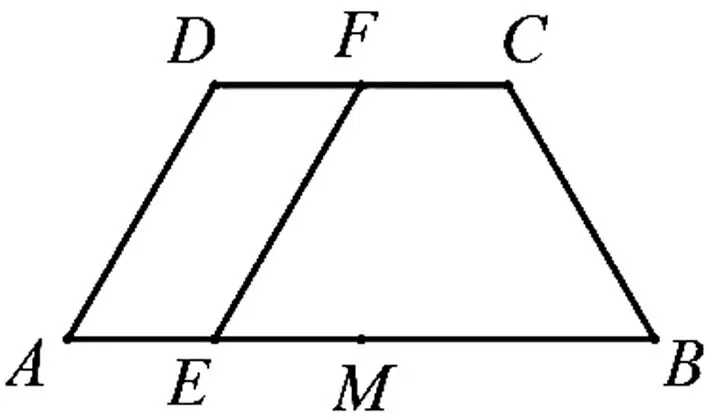
分析：根據題意，多面體ABCDEF是由等腰梯形ABCD翻折而成，翻折后BD的長度決定了翻折的角度，因此二面角D-EF-C的大小是我們分析幾何體結構的關鍵因素.

圖15

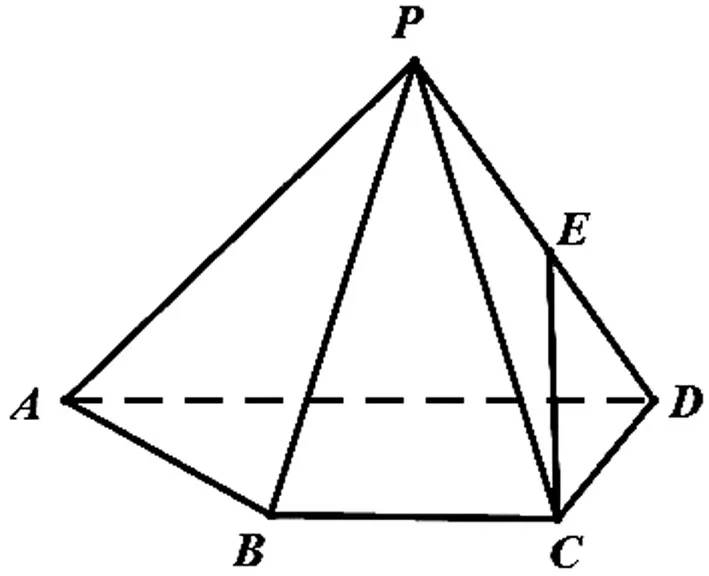
圖16

問題8如圖16，已知四棱錐P-ABCD，△PAD是以AD為斜邊的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E為PD的中點.

(Ⅰ)證明：CE∥平面PAB；

(Ⅱ)求直線CE與平面PBC所成角的正弦值.

分析：此問題是2017年浙江高考第19題，當年這題被稱為浙江省高考有史以來最難立體幾何題.許多考生由于對于此幾何體的結構把握不到位，導致幾何方法想不出，向量方法容易建錯坐標系.

圖17

該幾何體可以理解為：如圖17，平面內有一個由等腰直角三角形PAD和直角梯形ABCD構成的五邊形PABCD，將該五邊形沿AD翻折得到的幾何體就是四棱錐P-ABCD，其中PC的長度就是用來確定翻折的二面角大小.如果我們先分析五邊形PABCD不難發(fā)現，PB⊥AD，交點O即為AD的中點，翻折之后∠POB即為二面角P-AD-BC的平面角.而且容易證明BC⊥平面POB，進而平面POB⊥平面PBC.根據PC的長度我們可以確定∠POB=120°.要求直線CE與平面PBC所成角的正弦值，只需要求出點E到平面PBC的距離即可.接下來只需要取BC，PO的中點F，G，將CE平移至FG.這樣，就把E到平面PBC的距離轉化為G到平面PBC的距離，后面的計算就不再贅述.

轉化為常見的幾何體模型、用動態(tài)翻折的觀點看待幾何體，能夠加強學生對幾何體空間結構的分析能力，幫助他們形成對幾何體的整體認知，從而更好的探索幾何體中的垂直關系，進而發(fā)展他們的直觀想象這一核心素養(yǎng).