布站方式對(duì)基于TDOA的干擾源定位影響分析

胡人丹，常 青

(北京航空航天大學(xué)電子信息工程學(xué)院，北京 100083)

0 引言

隨著無(wú)線電技術(shù)的發(fā)展，電子信息戰(zhàn)是當(dāng)代社會(huì)戰(zhàn)爭(zhēng)的重要組成部分，如何識(shí)別和定位各種干擾成為了影響戰(zhàn)局的關(guān)鍵性因素[1]。定位通常分為有源定位和無(wú)源定位，有源定位是指系統(tǒng)自身發(fā)射信號(hào)，并通過(guò)信號(hào)的反射實(shí)現(xiàn)定位的方式；無(wú)源定位是在不發(fā)射電磁波的情況下，通過(guò)接收干擾源發(fā)射的信號(hào)實(shí)現(xiàn)定位的方式。無(wú)源定位技術(shù)與有源定位相比，擁有良好的隱蔽性，以及較強(qiáng)的戰(zhàn)場(chǎng)生存能力。

常用的無(wú)源定位技術(shù)有基于交叉測(cè)角(Angle of Arrival，AOA)的定位技術(shù)、基于到達(dá)時(shí)間(Time of Arrival，TOA)的定位技術(shù)[2]、基于到達(dá)頻率差(Frequency Difference of Arrival，F(xiàn)DOA)的定位技術(shù)[3]和基于信號(hào)到達(dá)時(shí)間差(Time Difference of Arrival，TDOA)的定位技術(shù)[4-5]。TDOA定位技術(shù)基于輻射源信號(hào)到達(dá)各接收站的時(shí)間差，一般需要多個(gè)接收站測(cè)量同一個(gè)輻射源信號(hào)的到達(dá)時(shí)間。通過(guò)信號(hào)到達(dá)的時(shí)間差可以計(jì)算出距離差，當(dāng)距離差為一個(gè)常數(shù)時(shí)，輻射源與接收站之間的位置關(guān)系就滿足一個(gè)雙曲線(面)方程[6]。在二維平面中，至少需要3個(gè)接收站才能計(jì)算出2個(gè)時(shí)間差，2個(gè)時(shí)間差就能得到2條雙曲線，而雙曲線的交點(diǎn)就是輻射源的位置。在三維空間中，至少需要4個(gè)接收站才能對(duì)干擾源進(jìn)行定位。雙曲線定位方法是一種較為精確的定位方法[7]，但也存在一些缺點(diǎn)，如當(dāng)2條雙曲線的交點(diǎn)不止一個(gè)時(shí)，就出現(xiàn)了模糊解問題。

在TDOA定位方式中，布站方式對(duì)模糊解區(qū)域的分布以及定位精度的影響很大[8]。在二維平面中，接收站之間的基線長(zhǎng)度和接收站之間的角度對(duì)模糊區(qū)域分布具有較大影響。在三維立體空間中，接收機(jī)布站的形狀和基線長(zhǎng)度對(duì)幾何精度因子(Geometric Dilution of Precision，GDOP)也有較大影響[9]。

本文針對(duì)TDOA定位方法中的布站問題，在二維平面對(duì)模糊區(qū)域進(jìn)行仿真，得到了模糊解區(qū)域分布與接收站布站之間的關(guān)系。通過(guò)公式推導(dǎo)可以得出接收站的布站方式對(duì)TDOA系統(tǒng)的定位精度有較大的影響。為了定量分析不同的布站情況對(duì)TDOA定位精度的影響，本文對(duì)四站三維接收站進(jìn)行了不同形狀的布站并進(jìn)行了仿真驗(yàn)證。仿真結(jié)果對(duì)實(shí)際工程應(yīng)用中的TDOA布站有較強(qiáng)的借鑒意義。

1 TDOA定位原理

1.1 TDOA定位算法

多站時(shí)差定位算法要在空間中對(duì)輻射源進(jìn)行定位，至少需要3個(gè)方程形成3個(gè)雙曲面，這就至少需要4個(gè)接收站同步完成輻射源信號(hào)TDOA的測(cè)量，定位原理如圖1所示。4個(gè)接收站中包括1個(gè)主站和3個(gè)輔站。

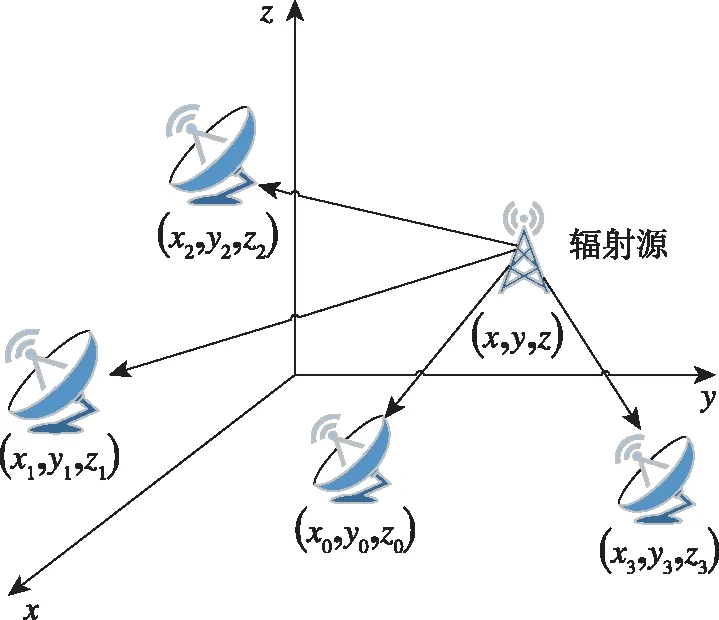
圖1 基于TDOA的無(wú)源定位系統(tǒng)示意圖Fig.1 Schematic diagram of passive location system based on TDOA

設(shè)待定的目標(biāo)位置為(x,y,z)T，主站坐標(biāo)為 (x0,y0,z0)T，輔站坐標(biāo)為(xi,yi,zi)T(i=1,2,3)，r0表示目標(biāo)到主站的距離，ri表示目標(biāo)到各測(cè)量輔站的距離。目標(biāo)到主站距離與到輔站距離的距離差為Δri，那么可得定位方程

(1)

式中，c為電波傳播速度；Δti為目標(biāo)信號(hào)到達(dá)第i個(gè)輔站與到達(dá)主站之間的時(shí)間差測(cè)量值；cΔti為第i個(gè)輔站到主站的距離差測(cè)量值。式(1)為一組關(guān)于目標(biāo)輻射源位置坐標(biāo)(x,y,z)的非線性方程組，目前有很多文獻(xiàn)研究了關(guān)于這個(gè)方程組的解法，如Chan氏算法[10]、泰勒級(jí)數(shù)展開法[11]、球面相交法[12]和去距離最小二乘法[13]等。其中Chan氏算法是求解雙曲線方程組的一種具有解析表達(dá)式解的非遞歸算法，該算法的特點(diǎn)是計(jì)算量小，無(wú)需做迭代運(yùn)算，并可得到較好的定位結(jié)果。

1.2 Chan氏算法定位模型

利用Chan氏算法對(duì)式(1)整理化簡(jiǎn)可得

(x0-xi)x+(y0-yi)y+(z0-zi)z=ki+r0Δri

(2)

其中

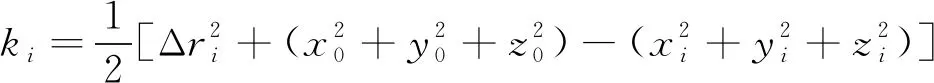
(3)

為求解這個(gè)方程組式，可先將r0看作一個(gè)已知量，因此可得如下矩陣表達(dá)式

AX=F

(4)

其中

(5)

X=[xyz]T

(6)

(7)

在合適的布置接收站的位置條件下，即主站與任意2個(gè)輔站不在一條直線上時(shí),rank(A)=3，用偽逆法求解方程(4)，可以得到

(8)

令

(9)

由式(8)可得

(10)

其中

(11)

在這里為了方便計(jì)算，假設(shè)x0=y0=z0=0，即參考主站的坐標(biāo)在原點(diǎn)。此時(shí)式(4)中的

(12)

(13)

其中

(14)

此時(shí)x、y、z的解為

(15)

其中

(16)

因?yàn)橹髡驹谧鴺?biāo)原點(diǎn)，因此可以得到

(17)

將式(15)代入式(17)得

(18)

其中

(19)

由式(18)可解得r0的2個(gè)根

(20)

將r0代入式(1)，即可得到目標(biāo)點(diǎn)的坐標(biāo)(x,y,z)。

2 GDOP定位精度分析

2.1 GDOP定位精度模型

對(duì)Δri=ri-r0兩邊同時(shí)取微分

dΔri=(Hix-H0x)dx+(Hiy-H0y)dy+

(Hiz-H0z)dz+(ki-k0), (i=1,2,3)

(21)

其中

(22)

ki=Hixdxi+Hiydyi+Hizdzi, (i=0,1,2,3)

(23)

寫成矢量形式為

dΔR=HdR+dS

(24)

其中主站與各輔站TDOA測(cè)量引入的誤差為

dΔR=[dΔr1dΔr2dΔr3]T

(25)

欲求的目標(biāo)定位誤差為

dR=[dxdydz]T

(26)

各站站址引入的測(cè)量誤差為

dS=[k1-k0k2-k0k3-k0]T

(27)

其中

(28)

由式(28)可得定位誤差估計(jì)值的最小二乘解

(29)

由式(29)可知,目標(biāo)定位誤差(dxdydz)T與時(shí)差測(cè)量誤差dΔR、站址測(cè)量誤差dS及目標(biāo)相對(duì)各站位置有關(guān)。由于各時(shí)間差測(cè)量信息中都包含有主站測(cè)量信息，即各時(shí)間差誤差中都包含有共同的誤差因素，因此各Δri的測(cè)量誤差是相關(guān)的[14]。設(shè)Δri測(cè)量誤差經(jīng)系統(tǒng)修正后是零均值的，而站址誤差在每次測(cè)量中是保持不變的，且站址誤差各元素之間及各站址誤差間互不相關(guān)，則定位誤差協(xié)方差為

Pdr=E[dRdRT]

=C{E[dΔRdΔRT]+E[dSdST]}CT

(30)

式中

C=(HTH)-1HT=[cij]3×3

(31)

E[dΔRdΔRT]=

(32)

E[dSdST]=

(33)

其中，σΔri為第i個(gè)輔站與主站之間的測(cè)量誤差標(biāo)準(zhǔn)差;ηij表示Δri與Δrj之間的相關(guān)系數(shù)

(34)

σxi、σyi、σzi為各站址測(cè)量誤差分量的標(biāo)準(zhǔn)差。假設(shè)各站址測(cè)量誤差標(biāo)準(zhǔn)差相同，即

(35)

又因?yàn)?/p>

(36)

可得

(37)

令

[eij]3×3=E[dΔrdΔrT]+E[dSdST]

(38)

[eij]3×3=

(39)

[eij]3×3=

(40)

由此可得定位誤差在x、y、z上的方差分別為

(41)

則

(42)

2.2 定位無(wú)解區(qū)與定位模糊區(qū)原因分析

對(duì)關(guān)于r0的一元二次方程ar02+br0+c=0進(jìn)行求解，可以得到r0的數(shù)值解。根據(jù)一元二次方程的特點(diǎn)，可以從解的情來(lái)進(jìn)行分析[15]。

1)Δ=b2-4ac<0時(shí)，方程的解為2個(gè)虛數(shù)，方程無(wú)實(shí)數(shù)解，無(wú)法準(zhǔn)確定位。

2)Δ=b2-4ac=0時(shí)，方程有唯一解，能夠準(zhǔn)確定位且定位結(jié)果唯一。

3)Δ=b2-4ac>0時(shí)，方程有2個(gè)解r01和r02，此時(shí)又可以分為以下兩種情況：

(1)r01r02<0，取r01和r02中正值為定位結(jié)果；

(2)r01r02>0，若r01和r02都為正，則此時(shí)出現(xiàn)了定位模糊，需要借助一定手段來(lái)消除定位模糊。

在實(shí)際系統(tǒng)中，由于噪聲干擾、多路徑傳輸和信道環(huán)境惡劣等原因?qū)е碌臅r(shí)差測(cè)量誤差不可避免。時(shí)差測(cè)量誤差使原本相交的雙曲線出現(xiàn)偏移，進(jìn)而導(dǎo)致出現(xiàn)無(wú)解情況。

3 仿真驗(yàn)證

3.1 平面三站系統(tǒng)模糊度仿真

如圖2所示，以主站S0為坐標(biāo)原點(diǎn)建立坐標(biāo)系，輔站S1到主站S0之間的距離為L(zhǎng)1，輔站S2到主站S0之間的距離為L(zhǎng)2。L1與L2之間的夾角為θ，L1和L2的長(zhǎng)度為基線長(zhǎng)度。

對(duì)圖2所示的時(shí)差定位系統(tǒng)在不同布站形式下的模糊度進(jìn)行仿真，分別將夾角設(shè)置為60°、90°和120°，同時(shí)改變基線長(zhǎng)度，設(shè)置坐標(biāo)如表1所示。仿真假設(shè)X、Y坐標(biāo)范圍均為[-200,200]，單位為km，仿真結(jié)果如圖3～圖8所示。

表1 不同條件下接收站位置坐標(biāo)

圖3和圖4為夾角60°時(shí)基線長(zhǎng)度分別為10km和20km布站條件下的模糊區(qū)域分布情況；圖5和圖6為夾角90°時(shí)基線長(zhǎng)度分別為10km和20km布站條件下的模糊區(qū)域分布情況；圖7和圖8為夾角120°時(shí)基線長(zhǎng)度分別為10km和20km布站條件下的模糊區(qū)域分布情況，圖中藍(lán)色的點(diǎn)為定位模糊點(diǎn)。通過(guò)對(duì)比圖3和圖4可以得到，基線長(zhǎng)度增加，模糊區(qū)域減小；通過(guò)對(duì)比圖3、圖5和圖7可

以得到，模糊區(qū)域主要分布在基線延長(zhǎng)線及其夾角區(qū)域。接收站輔站與主站形成的夾角增大，則主站上方的無(wú)模糊區(qū)域增加，主站下方延長(zhǎng)線形成的模糊區(qū)域也增加。

圖3 夾角為60°基線長(zhǎng)度為10km的模糊區(qū)Fig.3 Fuzzy area with the included angle of 60 degrees and the baseline length of 10km

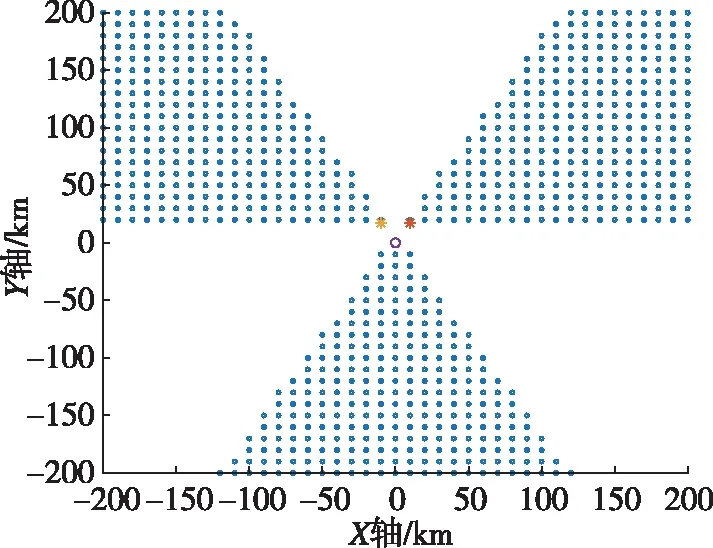
圖4 夾角為60°基線長(zhǎng)度為20km的模糊區(qū)Fig.4 Fuzzy area with the included angle of 60 degrees and the baseline length of 20km

圖5 夾角為90°基線長(zhǎng)度為10km的模糊區(qū)Fig.5 Fuzzy area with the included angle of 90 degrees and the baseline length of 10km

圖6 夾角為90°基線長(zhǎng)度為20km的模糊區(qū)Fig.6 Fuzzy area with the included angle of 90 degrees and the baseline length of 20km

圖7 夾角為120°基線長(zhǎng)度為10km的模糊區(qū)Fig.7 Fuzzy area with the included angle of 120 degrees and the baseline length of 10km

圖8 夾角為120°基線長(zhǎng)度為20km的模糊區(qū)Fig.8 Fuzzy area with the included angle of 120 degrees and the baseline length of 20km

3.2 四站三維系統(tǒng)精度仿真

決定定位精度大小的因素包括：站址測(cè)量誤差標(biāo)準(zhǔn)差、各接收站與目標(biāo)輻射源的幾何位置、接收站的布站方式和時(shí)差測(cè)量誤差標(biāo)準(zhǔn)差等。其中對(duì)定位精度影響最大的因素是各接收站與目標(biāo)輻射源之間的幾何位置關(guān)系[16]。通過(guò)觀察GDOP的表達(dá)式可以看出，GDOP的物理意義為3個(gè)坐標(biāo)軸方向上的測(cè)量誤差，因此GDOP越小，誤差越小，測(cè)量精度越高。下面對(duì)三種最常見的布站方式進(jìn)行GDOP仿真，這三種布站方式分別是：菱形、Y形和T形。各站坐標(biāo)如表2所示。

表2 不同形狀下接收站位置坐標(biāo)

仿真假設(shè)X、Y坐標(biāo)范圍均為[-300,300]，單位為km，時(shí)差測(cè)量精度固定為10ns，仿真結(jié)果如圖9～圖14所示。

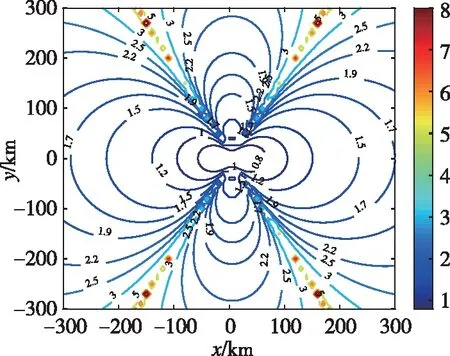
圖9 基線長(zhǎng)度為10km菱形布站下的GDOP分布Fig.9 The GDOP distribution under the rhombus station with a baseline length of 10km

圖10 基線長(zhǎng)度為20km菱形布站的GDOP分布Fig.10 The GDOP distribution under the rhombus station with a baseline length of 20km

圖11 基線長(zhǎng)度為10km Y形布站的GDOP分布Fig.11 The GDOP distribution with a baseline length of 10km Y shaped station

圖12 基線長(zhǎng)度為20km Y形布站的GDOP分布Fig.12 The GDOP distribution with a baseline length of 20km Y shaped station

圖13 基線長(zhǎng)度為10km T形布站的GDOP分布Fig.13 The GDOP distribution with a baseline length of 10km T shaped station

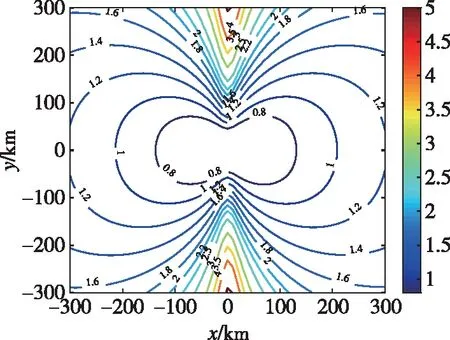
圖14 基線長(zhǎng)度為20km T形布站的GDOP分布Fig.14 The GDOP distribution with a baseline length of 20km T shaped station

圖9和圖10分別為基線長(zhǎng)度為10km和20km時(shí)菱形布站下的GDOP分布，通過(guò)觀察可以得到：基線長(zhǎng)度越長(zhǎng)，在相同坐標(biāo)點(diǎn)的GDOP越小，定位精度越高。圖11和圖12分別為基線長(zhǎng)度為10km和20km時(shí)Y形布站下的GDOP分布，圖13和圖14分別為基線長(zhǎng)度為10km和20km時(shí)T形布站下的GDOP分布，通過(guò)對(duì)比圖9、圖11和圖12可知，在相同基線長(zhǎng)度下，Y形布站各個(gè)方向的GDOP分布較為均勻；菱形布站在對(duì)角線連線區(qū)域定位精度較高，在基線延長(zhǎng)線方向定位精度較低；T形布站在三站在同一條延長(zhǎng)線方向上的定位精度較高，在其垂直方向定位精度較低。

4 結(jié)論

本文針對(duì)無(wú)源時(shí)差定位原理及精度進(jìn)行了理論分析，仿真了二維不同布站條件下的模糊區(qū)域分布，以及四站三維不同布站條件下的GDOP分布。仿真結(jié)果表明：

1)二維模糊區(qū)域分布由基線長(zhǎng)度和基線夾角所決定，模糊區(qū)域主要分布在基線延長(zhǎng)線夾角區(qū)域。

2)通過(guò)觀察四站三維不同形狀的接收機(jī)布站可以得到，在相同布站形狀下基線長(zhǎng)度越長(zhǎng)，同樣位置的GDOP越小。在實(shí)際布站時(shí)，將接收站之間的距離布置的稍微寬一點(diǎn)有利于提高定位精度。

3)在四站三維接收機(jī)布站條件下，同樣的基線長(zhǎng)度，Y形布站在各個(gè)方向的定位精度都較好，且較為均勻；菱形布站在接收站延長(zhǎng)線方向的定位精度較好，在接收站延長(zhǎng)線夾角方向的定位精度較差；T形布站在三站在同一條延長(zhǎng)線方向上的定位精度較好。當(dāng)不確定輻射源位置時(shí)，用Y形布站較為合理。