聚焦本質 多元探索
——《圓的面積》教學設計（二）

文|王小波

【教學內容】

人教版六年級上冊第67、68 頁。

【教學過程】

一、課前探究，喚醒轉化意識

課前，教師布置前置性作業：

上課之前，教師收集學生的《研究單》，獲知大多數學生都想到了要把圓的面積轉化成已經學過的圖形的面積。

【設計意圖：求圓的面積對于學生來說是困難的，相較于以前學過的平面圖形，它不容易轉化，但那些平面圖形面積推導時運用到的“轉化”思想早已在學生的心中打上了深深的烙印。課前研究給學生足夠的時間和空間，讓他們能夠像數學家一樣地思考，親歷探究“圓的面積”的求解過程，形成豐富的個體經驗，為課中的深度對話交流做好準備。】

二、課內研習，感悟轉化思想

1.組內研習，初步感知“轉化”思想。

師：關于“圓的面積”，大家已經做了課前研究，現在小組內把你想到的方法、遇到的困難以及如何解決進行分享。

（聚焦其中一個小組）

組長：我想到了轉化成長方形，因為平行四邊形、三角形等圖形的面積都是轉化成長方形的。

組員1：我也是轉化的。剛開始我還想畫上“格子”，用數格子的方法數出圓的面積，但我遇到了困難：我發現圓是曲線圖形，外面的部分沒法數。所以我就想，怎么把圓轉化成規則圖形呢？

組員2：我就是轉化的，我把圓形紙片平均剪成了8 個小扇形，再把它們一正一反地拼在一起，拼成了一個平行四邊形。

組員1：這個不是平行四邊形。平行四邊形的邊是直的，你這個上下都是有圓弧的。

組員3：我也發現了這個問題，后來我發現把這些扇形再繼續平均分，圓弧就越來越小。所以，我就把圓形當作一個近似的平行四邊形來計算。

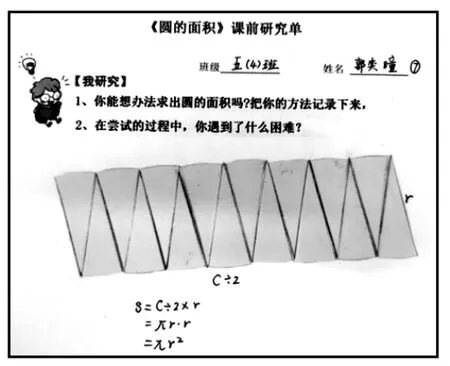
組長：我們分得份數越多，就會越接近一個平行四邊形。那這個平行四邊形的面積要怎么求呢？底和高分別是什么？

組員3：平行四邊形的底就是圓周長的一半，這個我們可以從圖上看出來，我作出它的高，發現平行四邊形的高就是圓的半徑。

組員1：把最左邊的一個扇形從中間剪開拼到右邊，就轉化成了長方形，長方形的長和寬分別是圓周長的一半和半徑，所以圓的面積是化簡一下是πr2。

【設計意圖：教師深入小組中仔細聆聽小組內討論的過程。盡管每個小組學生的情況不盡相同，討論的方法和深度也不完全一致。但相似的是，經過了課前充分地探究，小組交流時，已經能夠全身心投入其中，借助所有組員的力量，全方位地進行思想的碰撞：把自己的困惑提出來，小組內的成員說出自己的看法，盡可能嘗試解決問題。盡管此時，也許有學生的理解還是“囫圇吞棗”，對知識點不夠清晰明了，經其他組員的點撥，已經略有所悟，這些都為全班的交流打下了基礎。】

2.全班交流，進一步深化“轉化”思想。

師：剛才每個小組都進行了深入的交流，有的組甚至交流出了多種不同的轉化方法，下面全班來理一理《研究單》中的問題。

生：我們組想到了轉化的方法，把圓形紙片平均剪成若干個小扇形，穿插在一起，拼成了近似的平行四邊形。平行四邊形的底和高分別是和r，所以，圓的面積是πr2。我們的困惑是，這個面積到底是近似的還是準確的？

師：這個困惑解決了嗎？

生：剛開始，我覺得是近似的，但我們組討論后發現，如果平均分的扇形越來越小，它是接近三角形的，所以如果分得足夠多，拼成的應該就是平行四邊形。

師：其他組有什么想法嗎？

生：我覺得你說得還不夠準確，如果平均分的份數無限多，就會拼成一個長方形。

師：我們發現，分的份數越多，小圓弧將會越短，但是像這樣繼續分下去，拼成的圖形會變成長方形嗎？

師：我這有張圓形紙片，誰來平均分成256 份試試看？

（學生紛紛表示，分成256 份太麻煩了，實際操作會有誤差）

師：我們可以請電腦來幫忙，你們任意說平均分的份數，我們用“幾何畫板”來進行操作。

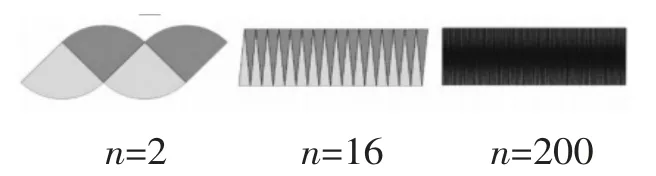
注：2n 表示平均分的份數。

師：你發現了什么？

生：現在是200 份，拼成的圖形已經非常接近長方形了，如果真的是無數份的話，拼成的就是長方形了。

生：原來我拼成的是平行四邊形，我想到平行四邊形可以剪下一個三角形平移拼成長方形，也可以把圓轉化成長方形的，現在我知道了，其實不用進一步轉化，份數足夠多時，拼成的就是長方形。

師：看來大家已經體會到如何把圓轉化成長方形了，那么圓面積的計算公式怎樣推導呢？

生：長方形的長相當于圓周長的一半，寬相當于圓的半徑，因此圓的面積公式是πr2。

師：那么圓是不是只能轉化成長方形呢？你們小組是怎樣探究的？

生1：我把圓形紙片平均分成16 份，拼成了一個梯形，梯形的上底和下底的和是8 個小圓弧，也就是圓周長的一半，梯形的高是2個圓半徑的長度，因此，圓面積就是C÷2×2r÷2，化簡后也是πr2。

生2：我是把圓平均分成了9份，拼成一個三角形，三角形的底是3 個圓弧的長，也就是圓周長的，高是3 個圓半徑的長度，所以圓面積就是

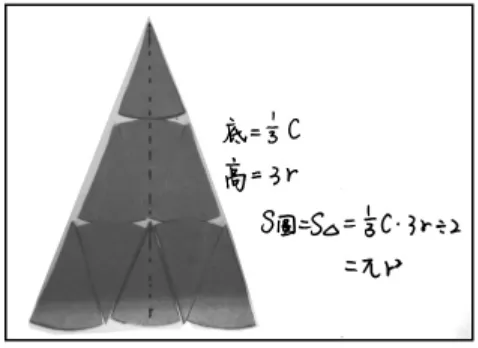
生3：我還有不同的方法。我把圓片平均分成8 份，1 份是一個近似的三角形，底是圓周長的，高是圓半徑的長度。一個三角形的面積是，8 個三角形就是

師：同學們真厲害，利用梯形、三角形的面積也推導出了圓的面積，圓等分之后還能拼成其他圖形，比如說組合圖形。

生：我們組剛開始就是拼成組合圖形，但是求面積太麻煩了。

師：那么眾多的轉化方法中，你會優先選擇哪種呢？

生：當然是長方形，它是所有圖形的基礎，也是最容易推導的。

【設計意圖：把圓的面積轉化成長方形是最常見、最理所當然的。然而這并不意味著一想到轉化，學生就會想到轉化成長方形，也不見得就能轉化成功。在課堂上，學生拋出“轉化成的面積是準確的還是近似的？”這個問題，在討論中借助動畫的演示，學生體會到“極限”思想。在匯報時，學生的思維發散到轉化成不同的平面圖形來求圓的面積，不再局限于教材的表面處，而是基于學生的元認知，創新于教材的潛隱處。自主的探究加上課堂中充分地表達，讓每一位學生都卷入其中，學有所悟，深刻領悟了轉化思想：把復雜的內容簡單化，陌生的內容熟悉化。用好轉化思想，讓數學學習更加智慧、更加靈動。】

三、創新練習，運用轉化方法

師：知道了圓面積的計算公式，我們試著來解決一些問題。

【設計意圖：練習的設計都是求圓的面積，但難度層層遞進，可以滿足不同水平學生的需求。其中第2 題，更是要求學生能夠判斷出大圓和小圓面積之間的關系，從而解決生活中的實際問題，對學生知識的掌握以及能力的提升都大有幫助。】

四、全課小結

（略）