分有法，合有道
——《分數(shù)的意義》教學(xué)策略例談

陳 燕

(江蘇省淮安市老壩口小學(xué) 江蘇 淮安 223001)

1.分有法

1.1 單位“1”教學(xué)策略例談。在之前的學(xué)習(xí)中，學(xué)生已經(jīng)陸續(xù)了解到可以將一個物體平均分，也可以將一些物體組成的整體平均分。盡管如此，單位“1”的認識對學(xué)生來說仍是有距離感且不易理解的。因此，如何將單位“1”的概念抽象出來，是教師急需要解決的問題。

(1)策略一：從1到“1”，巧識單位“1”

出示：一個月餅，一張白紙，一把1米長的尺子

師：都可以用自然數(shù)幾來表示？生：1

師：你認為自然數(shù)1還可以表示什么？生：一個整體

師：(抓起一把粉筆)能用1表示嗎？生：1把粉筆

師：(一疊白紙)，能用1表示嗎？生：1疊白紙

師：(出示12條金魚，99朵玫瑰， 40分鐘)……

生：一群金魚、一束玫瑰、一節(jié)課……

師：現(xiàn)在你對1又有了什么認識？

生：1可以表示一個物體、一個整體、一個計量單位……

師：像這樣的一個物體、一個整體、一個計量單位都可以看作為單位“1”。

師：1上面為什么加引號？

生：說明這里的1并不僅僅是一個物體，也有可能是許多物體組成的一個整體……

師：單位“1”還可以表示什么？現(xiàn)在你可以把什么看作單位“1”？

在這一段的教學(xué)中，教者能從1入手，先讓學(xué)生用1來描述相關(guān)事物，如1個物體、1個整體、1節(jié)課、1把粉筆等等，讓學(xué)生在描述中體會到無論是1個物體，還是由許多物體，都可以用1來表示，擴大了1的范圍；接著將學(xué)生認識到的這些1抽象概括成單位“1”，并通過1和“1”的對比讓學(xué)生明確，單位“1”不同于1，是因為其有著更為豐富的內(nèi)涵：它不僅僅可以表示1個物體，更可以表示其它內(nèi)容。而1與“1”的對比，則讓學(xué)生進一步明確了它們的異同，讓學(xué)生在對比中明確：“1”并不是真正的1，因為其所指向的對象更為豐富，數(shù)量上也突破了1的局限性。

(2)策略二：從分到合，分出單位“1”

單位“1”所能概括的事物非常廣泛，教材中給出了一個物體、一個計量單位、一個整體的例舉。對學(xué)生來說，學(xué)生所認識的單位“1”則更為詳細具體，比如一個蘋果、一盤桃子、一張紙、一瓶水等等，這些事物往往都非常詳細、具體。而分類，可以很好的幫助學(xué)生從這些具體的事物中概括總結(jié)出普遍性規(guī)律，有助于學(xué)生歸納形成對單位“1”的認識。

師：出示四幅圖，你能用分數(shù)表示圖中涂色部分嗎？

同桌互相說一說。

指名兩人板演并說一說每個分數(shù)的含義。

師：你能依次說一說這幾個分數(shù)分別是將什么平均分呢？

學(xué)生口答，教師根據(jù)口答板貼均分事物的圖片。

師：你能將這些對象分分類嗎？

學(xué)生嘗試將黑板中的圖片分分類。

根據(jù)學(xué)生分類情況依次總結(jié)：一個物體、一個計量單位、一個整體

師：如果讓你用一個字來表示，你想到了什么？

生：1

師：像這樣的一個物體、一個計量單位、一個整體，都可以看作是單位“1”。

師：為什么1要加雙引號?生活中還有什么可以看作單位“1”？

單位“1”有著極其豐富的內(nèi)涵，如何讓學(xué)生認識并理解這樣的內(nèi)涵呢？教者分成了這樣的兩個層次：首先，出示豐富的素材，讓學(xué)生根據(jù)圖片說一說各可以用哪個分數(shù)表示，以及這個分數(shù)的具體含義。直觀的圖片為學(xué)生認識其豐富性提供了可能，讓學(xué)生在觀察、討論、交流中明晰不同的分數(shù)是將不同的事物進行平均分；其次，教者將上述均分的物體展現(xiàn)出來，引導(dǎo)學(xué)生將他們分分類。讓學(xué)生在分類比較的過程中進一步體會單位“1”的豐富性，并且順理成章地概括出“一個物體、一個計量單位、一個整體”，在這樣的概括的過程中掌握單位“1”的含義。

策略三：以退為進，猜出單位“1”

師：出示四分之三，說一說表示什么意思？

問：四分之三可以把什么平均分？

學(xué)生口答：一個蘋果、一個月餅、一塊蛋糕……

師：一個盒子，里面裝著想平均分的物體，猜一猜是什么？

根據(jù)學(xué)生猜測依次出示一個月餅，一個長方形，一個1米線段，8個蘋果等。

師：(指著8個蘋果)這還是一個物體嗎？

介紹：一個整體

師：還可以將什么平均分？

學(xué)生口答：一個班的學(xué)生、一筐蘋果……

該策略充分利用學(xué)生已有的認知經(jīng)驗，讓學(xué)生從熟悉的分數(shù)“四分之三”入手，先說一說它的含義，再推想“四分之三”可以將哪些物體平均分？學(xué)生在交流的過程中會突破思維的局限性，如根據(jù)“一盤桃子”可以聯(lián)想到“一籃桃子”、“一筐桃子”、“一車桃子”等等，這樣的聯(lián)想是可貴的，讓學(xué)生充分體會到單位“1”表述事物的廣泛性。接著教者又進一步拓展延伸，提出問題：“還可以將什么平均分？”在學(xué)生在群體交流中進一步體會單位“1”包含事物的廣泛性。

2.合有道

2.1 借助數(shù)軸圖，巧妙識分數(shù)。分數(shù)是數(shù)的世界中不可或缺的一部分。對五年級的學(xué)生來說，學(xué)生并非初識分數(shù)，也并非初識數(shù)軸圖。之前認識小數(shù)、正數(shù)和負數(shù)時，就曾借助于數(shù)軸圖來認識。數(shù)軸圖可以幫助學(xué)生找準(zhǔn)數(shù)與點之間的對應(yīng)關(guān)系。借助數(shù)軸圖來認識分數(shù)，不但可以幫助學(xué)生更好地理解分數(shù)的意義，還可以讓學(xué)生對數(shù)的構(gòu)成有更為清晰的認識。但是，如何讓學(xué)生理解并接受相對抽象的數(shù)軸圖呢？

策略一：分層認識數(shù)軸圖

數(shù)軸是由原點、單位長度、方向(一般規(guī)定向右為正)組成的直線。在數(shù)軸上，一個單位長度即對應(yīng)分數(shù)意義中的單位“1”，這樣的對應(yīng)關(guān)系對學(xué)生來說是有著一定的難度的。因此教者可采取分層推進的方法，將數(shù)軸圖進行分解，這樣學(xué)生的理解就會變得容易得多。

師：出示數(shù)軸圖，標(biāo)注出一個單位長度。

學(xué)生理解并回答：這樣的一個單位長度表示單位“1”。

繼續(xù)出示同樣單位長度的線段兩段、三段……

學(xué)生理解并回答：兩個單位長度表示2，三個單位長度表示3……

多媒體演示，將若干個單位長度的線段連接起來，填上原點和方向，形成數(shù)軸圖。

要求學(xué)生依次在數(shù)軸圖上找一找分數(shù)，并說明自己的原因。

在上述教學(xué)環(huán)節(jié)中，教者先是從一個單位長度的線段入手，將學(xué)生將一個單位長度和單位“1”相對應(yīng)，明確將一個單位長度的線段均分成幾份，其中的一份或幾份就表示幾分之一或幾分之一。這實際上也是對真分數(shù)的認識過程；接著，教者突破了學(xué)生認識局限，從一個單位長度到幾個單位長度，并結(jié)合多媒體將數(shù)軸圖的形成過程展現(xiàn)了出來，讓學(xué)生體會到無論對應(yīng)的份數(shù)是多少，其均分的份數(shù)仍以一個單位長度為標(biāo)準(zhǔn)，這實則也是對假分數(shù)和帶分數(shù)進行了初步的滲透。讓學(xué)生在分層的認識中親歷了數(shù)軸圖形成的過程和真、假分數(shù)形成的過程，既突出了數(shù)軸圖表示數(shù)據(jù)的特點，又幫助學(xué)生深化理解了分數(shù)的意義。

策略二：分段認識數(shù)軸圖

出示數(shù)軸圖，標(biāo)注出若干個單位長度。

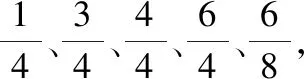
展示數(shù)軸圖及學(xué)生標(biāo)注的分數(shù)。

師：觀察這些分數(shù)及對應(yīng)的點，說一說你有什么發(fā)現(xiàn)？

生：前幾個分數(shù)的分母一樣，它們都表示把單位“1”平均分成4份；最后一個分數(shù)表示把單位“1”平均分成8份。平均分的份數(shù)不同，分母也就不同；

生2：表示把單位“1”平均分成4份，表示這樣1份的數(shù)；其它的分數(shù)依次表示這樣的3份、4份和6份；

師：說一說它們分別在數(shù)字幾和幾之間？你是怎么理解的？

生：依次說明。

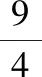
數(shù)軸圖上，每一段所表示的數(shù)據(jù)的大小是完全不同的。在上述教學(xué)環(huán)節(jié)中，教者采取分段認識數(shù)軸圖的方式，先引導(dǎo)學(xué)生認識了0與1這一段之間的分數(shù)，再逐步引申到其他分數(shù)。分段認識的方式讓學(xué)生對分母和分子所表示的意義有了更深刻的認識，也初步滲透了真、假分數(shù)及分數(shù)與整數(shù)、帶分數(shù)互化的初步知識，為學(xué)生的后續(xù)學(xué)習(xí)奠定基礎(chǔ)。

分數(shù)之所以叫做分數(shù)，是因為其是由“分”而來，3000多年前，古埃及為了在不能分得整數(shù)的情況下表示數(shù)，用特殊符號表示分子為1的分數(shù)。2000多年前，中國有了分數(shù)，但是，秦漢時期的分數(shù)的表現(xiàn)形式跟現(xiàn)在不一樣。后來，印度出現(xiàn)了和我國相似的分數(shù)表示法。再往后，阿拉伯人發(fā)明了分數(shù)線，今天分數(shù)的表示法就由此而來。分數(shù)是度量和數(shù)學(xué)本身的需要——除法運算的需要而產(chǎn)生的。讓學(xué)生更好地理解分數(shù)的意義，必須讓學(xué)生親歷“分”和“取”的過程，“分之有法，取之有道”，在“分-合”的過程中理解分數(shù)的本質(zhì)，才能讓學(xué)生的學(xué)習(xí)有根有源，有本有章，才能讓學(xué)習(xí)真正立足于學(xué)生需求。