基于FP-Growth算法的高校學生公共課成績與專業課成績相關性研究

余弦，周誼芬

（南通大學a.杏林學院，b.醫學院，江蘇 南通 226000）

高校人才培養方案中所計劃開設的課程，一般可分為公共課（包含公共選修課和公共必修課）和專業課（包含專業基礎課和專業課）兩種[1]。一般而言，公共課和專業課之間有一定的相關性，公共課所學習的內容在一定程度上是專業課內容的基礎，熟悉公共課知識對掌握專業課內容具有促進作用[2]，但是否每一門公共課的成績都會對相關專業課的成績產生影響，以及會產生多大的影響，仍有待研究和驗證。

隨著信息技術的快速發展，數據挖掘及相關技術在高校的教學、科研等領域得到不斷拓展應用。數據挖掘技術在尋找海量數據的內在關聯規則方面具有效率高、適用靈活等優點。在教學過程中累積的學生成績已經形成一個體量龐大的數據庫，通過數據挖掘的相關算法來尋找大量學生成績數據之間潛在的關聯規律，進而提高高校課程設置合理性和學生學習效率，已經成為高等教育管理領域的研究熱點之一[3]。應用FPGrowth算法對某高校部分計算機專業學生的公共課成績和專業課成績進行相關性分析，針對二者的關聯程度展開實證研究，為高校教學計劃的課程設置和教學改革提供有力的科學依據。

1 FP-Growth算法原理和實現

FP-Growth(Frequent Pattern Tree,頻繁模式樹)算法是一種在經典Apriori算法基礎上演變而來的挖掘頻繁項集方法[4]。它針對Apriori算法運行效率較低，實現過程中需要多次掃描整個事務集，進而產生大量候選集的缺點做了明顯的改進。FP-Growth算法比Apriori算法效率更高，它將數據集存儲于一個按特定順序構成的樹結構（FP樹），通過構建FP樹來壓縮事務數據庫中的信息，從而更加有效地產生頻繁項集[5]。在整個算法執行過程中，只需遍歷事務集兩次，通過遞歸調用FP樹結構，刪除不符合最小支持度（關聯度低）的項目，直至最終形成單一的樹結構，就能夠完成頻繁模式的發現。其發現頻繁項集的基本過程如下。

將事務數據庫中的單個事務記為Tk，而T={T1,T2,...,Tk}是所有事務的集合。事務中所包含的各個項目記為Ik，所有項目的集合I={I1,I2,...,Ik}。FP-Growth算法首先掃描一遍事務集T，計算事務集T中各項目Ik出現的次數n，并設定最小支持度s（項目出現的最少次數），若項目集I中某個項目Ik的出現次數n小于最小支持度s，則刪除該項目，然后將原始事務集T中的各項事務Tk按項目集Ik中的項目頻次進行降序排列。之后第二次掃描事務集T，創建項頭表以及FP樹。項頭表的第一列是按照降序排列的頻繁項，第二列是指向該頻繁項在FP樹中節點位置的指針[6]。FP樹其實是一棵用來存儲項目出現次數的前綴樹，每個項目均以路徑的方式存儲在樹結構中，與其它樹形結構不同，各項目在FP樹中并非只出現一次。只有當項目和頻次均不一致時，樹結構才會分枝。項目每出現一次，若在FP樹中有同路徑的節點，則記數增加一次，若無同路徑的節點，則相應的新增該項目節點。最終各項目按支持度降序排列，支持度越高的頻繁項離根節點越近[7]，從而使得更多的頻繁項可以共享前綴。

FP樹構建完成之后，依照樹結構中從下往上的順序，對于每個項目找到其條件模式基（CPB，conditional patten base），遞歸調用樹結構，刪除小于最小支持度的項。如果最終呈現單一路徑的樹結構，則直接列舉所有組合；非單一路徑的則繼續調用樹結構，直到形成單一路徑，即可挖掘出項目的頻繁項集。

2 FP-Growth算法在分析學生公共課成績與專業課成績相關性中的應用

2.1 學生成績預處理及離散化

根據FP-Growth算法原理及其實現步驟，本文以某高校計算機專業2018級學生的成績為數據來源，研究學生公共課成績和專業課成績之間的相關性。根據該專業教學計劃的具體內容及培養重點，選擇高等數學A(一)、大學英語(一)、計算機導論三門課程成績作為公共課成績代表，另外選擇高級語言程序設計(C++)(一)、數據庫原理及應用、數據結構三門課程成績作為專業課成績代表，在不考慮學生補考或重修等異常考試的情況下，共得到有效學生成績數據418條，作為全部的數據來源。限于本文篇幅，隨機選取其中的15名學生數據作為研究實例，其公共課和專業課原始成績如表1所示。為保護學生個人信息，以學號后六位代表對應學生。

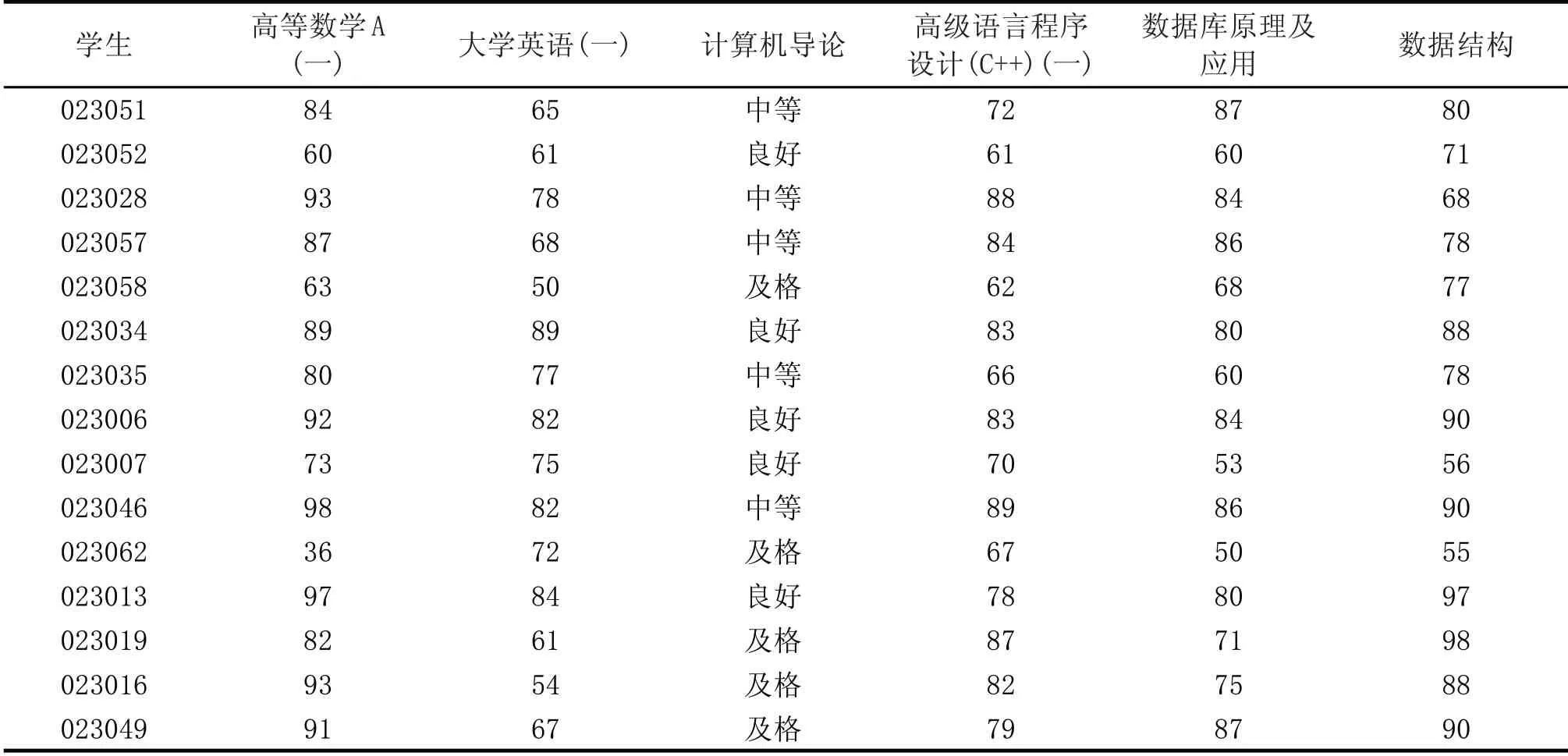
表1 學生公共課和專業課原始成績

學生的成績數據部分為百分制，部分為五級計分制，為方便FP-Growth算法處理，將學生成績數據做進一步的離散化處理。若某門課程成績為五級計分制的優秀或良好，或者其成績為百分制且分數大于等于80，則認為其成績優良，將其標注為Ik，反之則不標注。依此規則，將高等數學A(一)、大學英語(一)、計算機導論三門公共課成績為優良分別記作I1、I2、I3，高級語言程序設計(C++)(一)、數據庫原理及應用、數據結構三門專業課成績為優良分別記作I4、I5、I6。本文主要討論公共課成績優良與專業課成績優良之間的關系，故非優良的成績忽略不計。原始成績離散規則如表2所示。離散化后的學生公共課成績和專業課成績如表3所示。

表2 原始成績離散規則

表3 離散化后的學生公共課成績和專業課成績

2.2 學生公共課成績與專業課成績相關性分析

根據FP-Growth算法思想，通過以下步驟來完成學生公共課成績與專業課成績相關性分析。

1)將表3中離散化后的學生公共課成績和專業課成績作為事務集T，各項事務中所包含的項目的集合I={I1，I2，I3，I4，I5，I6}。首先完整地掃描一遍事務集T，計算所有學生成績數據中各成績項目Ik出現的次數n，得到的結果如表4所示。

表4 各成績項目Ik出現的次數

2)設定最小支持度s=5。項目集I中成績項目I2的出現次數n為4，小于最小支持度s，故刪除此項目。按出現頻次將項目集I重新排序為{I1，I6，I5，I4，I3}，依照此項目順序將成績事務集T中的各項事務Tk進行降序排列。刪除不符合最小支持度項目并進行降序排列前后的事務集T如表5所示。

表5 刪除不符合最小支持度項目并進行降序排列前后的事務集

3)掃描表5中經過刪除不符合最小支持度項目并進行降序排列之后的事務集T，創建項頭表以及FP樹。FP樹的根節點記為null，不表示任何項。先根據第一條事務T1={I1,I6,I5}創建FP樹的第一條分支，之后將事務T2到T13中的項目逐條插入FP樹中。若新加入的項目路徑若與現有FP樹節點相同，則原有節點數量增加一次；若新加入的項目路徑與FP樹節點不同，則FP樹分枝，增加新的項目節點。以此構建的項頭表和FP樹如圖1所示。

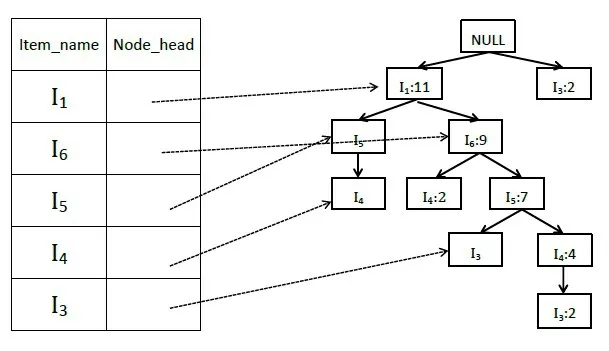
圖1 項頭表和FP樹

4)FP樹構建完成之后，查找每個項目對應的條件模式基。以項目I5和I6為例，I5的條件模式基為{I1}、{I1:7，I6:7}，I6的條件模式基為{I1:9}。將I5和I6的條件模式基作為新的事務數據庫，以條件模式基的項目為節點，構建I5和I6的條件FP樹如圖2所示。

由圖2可知，I5和I6的條件FP樹均為單路徑，且每一節點均滿足最小支持度，所以直接列舉條件FP樹中的所有節點組合，與對應項目取并集，即可得對應項目的頻繁項集。I5的條件FP樹節點組合為{I1:8}、{I6:7}、{I1:8，I6:7}，與I5取并集得到滿足最小支持度的頻繁項集為{（I1:8，I5:8），（I6:7，I5:7），（I1:7，I6:7，I5:7）}；同理，I6的條件FP樹節點組合為{I1:9}，與I6取并集得到滿足最小支持度的頻繁項集為{（I1:9，I6:9）}。

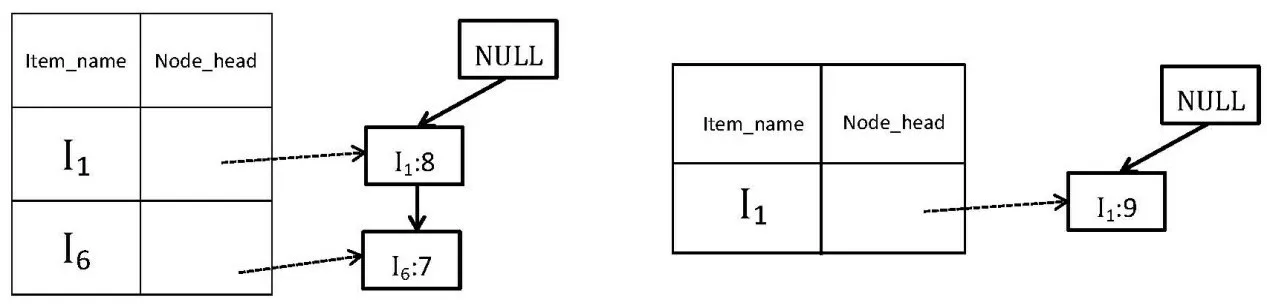
圖2 I5和I6的條件FP樹

據此分析，I1和I5以及I1和I6之間存在較強的關聯性。由此可以得出，如果學生的公共課高等數學A(一)的成績為優良，則其數據庫原理及應用、數據結構兩門專業課成績為優良的概率較大。而大學英語(一)和計算機導論兩門公共課成績未發現與數據庫原理及應用、數據結構兩門專業課成績存在明顯的關聯性。

3 結語

本文指出了高校學生公共課成績與專業課成績之間關聯的不確定性，通過分析數據挖掘的FP-Growth算法，以某高校計算機專業學生為例，選擇高等數學A(一)、大學英語(一)、計算機導論三門公共課成績和高級語言程序設計(C++)(一)、數據庫原理及應用、數據結構三門專業課成績為數據挖掘對象，將六門課程成績概化之后引入FP-Growth算法進行分析處理，通過構建FP樹等步驟，高效挖掘學生公共課成績與專業課成績之間的潛在關系，得出了兩者之間的關聯規則。這些關聯規則可以為高校教學單位課程設置提供有力的理論依據，進而制定更加科學合理的培養計劃，促進高校教學模式及人才培養過程的改革。學生也能以此為參考，結合自身成績特點，靈活調整學習重點，更有針對性地吸收知識，有效提高學習效率。