探究高中數學新教材中互補角的應用問題

江蘇省南京市臨江高級中學 樂曉梅

2020 級高一是蘇教版數學新教材使用的第一個學年，教師需要學好新課標、用好新教材，發現新教材中變化的方面，充分領悟編者的意圖，從而更好地為教學服務。三角形是所有幾何圖形的基礎，本文主要探究通過隱含的互補角，利用正、余弦定理解決三角形問題，在教學活動中發展學生的數學運算素養，進一步提高學生的數學思維品質。

一、運用互補角證明三角形中線長公式

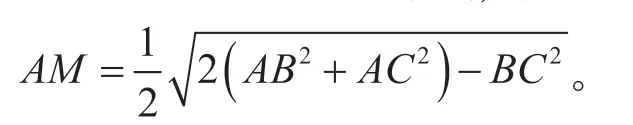
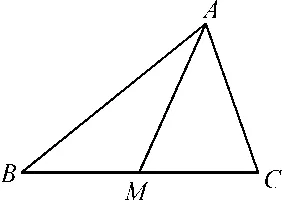
圖1

這道例題出現在余弦定理這一節，因為涉及邊的平方形式，等式結構特征明顯，很容易讓學生想到在三角形中運用余弦定理，又因為這些邊分布在兩個三角形中，所以分別在△AMB和△AMC中利用補角的余弦值相反，即cos ∠AMB=-cos ∠AMC。

二、運用互補角證明三角形角平分線定理

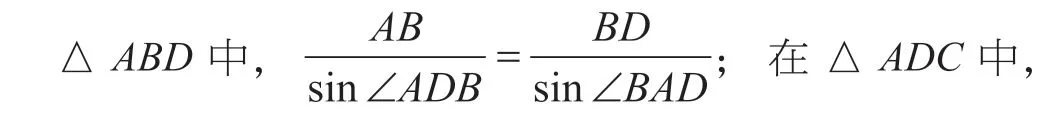
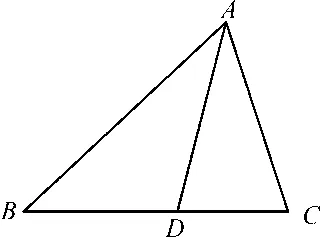
圖2

學生活動1：你能用平面幾何的方法來證明這個結論嗎？

與邊角有關，想到面積，探究面積法：

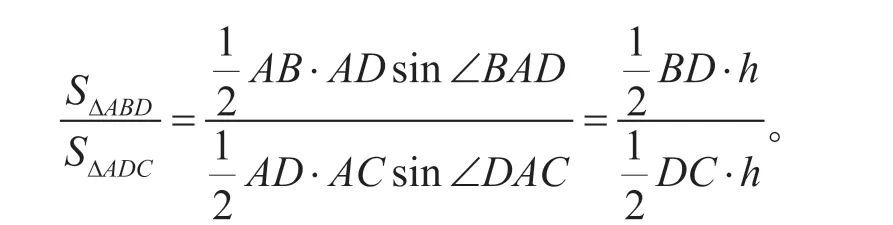
學生活動2：如果這個角平分線是外角的，會有什么結論呢？教材在95 頁思考運用部分第9 題，為學生創設了活動平臺。通過這些探究活動，讓學生發現問題、探究問題和解決問題的能力得以提升。

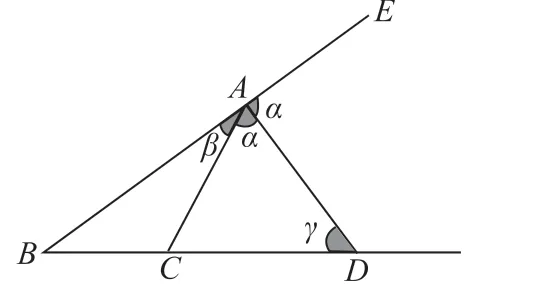
圖3

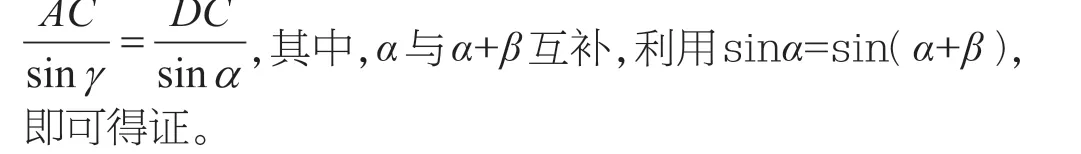
為了鞏固補角關系在圖形中的應用問題，編者在習題中設計了多個問題。

三、運用互補角求證四邊形中的相關問題

1.平行四邊形中對角線和邊的關系

學生分析：根據式子結構特征，出現邊的平方，易想到余弦定理，但三角形較多，要分別選擇以AC、BD為邊的三角形，我選擇△ABC和△BCD：

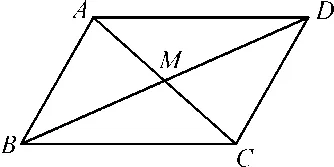
圖4

△ABC中，AC2=AB2+BC2-2AB·BCcos ∠ABC，

△BCD中，BD2=BC2+CD2-2BC·CDcos ∠BCD，

∠ABC與∠BCD互補，即cos ∠ABC=-cos ∠BCD，兩式相加即可得證。

余弦定理只能在三角形中使用，如何將四邊形轉化為三角形是關鍵，對四邊形進行分割會出現多個三角形，選擇哪些三角形又是一個關鍵點。在問題探索中加強了學生的分析能力。

2.圓的內接四邊形中求值問題

探究拓展1：教材89 頁第12 題。

（1）如圖5，圓O的內接四邊形ABCD，其中，AB=2，BC=6，CD=DA=4，求cosA的值。

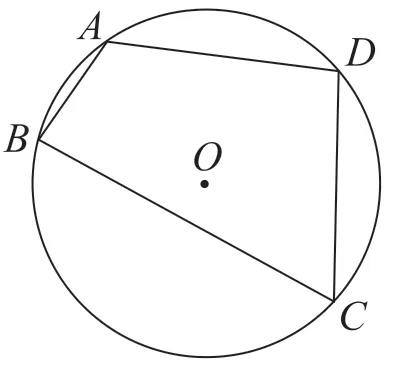
圖5

（2）已知圓的內接四邊形ABCD， 其 中，AB=a，BC=b，CD=c，DA=d，求cosA的值（用a，b，c，d表示）。

學生分析：連接BD，分別在△ABD和△BCD中利用余弦定理計算BD2，根據∠A與∠C互補，得到cosA=-cosC，兩式相減即可得證。

這道題第一問由具體四邊形出發，讓學生探究。在前面例題的基礎上，學生很容易想到分割四邊形放到三角形中，再由之前的補角應用，很容易算出數值，在此過程中，學生分析問題的能力、數學運算素養得到進一步發展。第二問是新增內容，由特殊到一般，比較抽象，但在第一問鋪墊的基礎上，很容易發現還是分別在△ABD和△BCD中利用余弦定理計算BD2，根據∠A與∠C互補，得到cosA=-cosC，兩式相減即可得證。這也是數學上常用的方法，特殊化探究出一般結論。

探究拓展2：教材105 頁復習題探究拓展第10 題。

（1）如圖6，在圓O的內接四邊形ABCD中，AB=2，BC=6，CD=DA=4，求四邊形ABCD的面積。

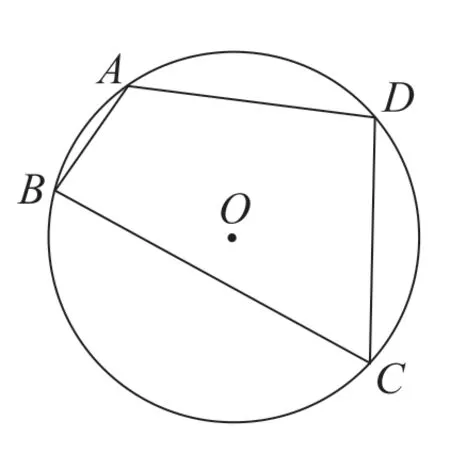
圖6

這兩道探究拓展題的題干是一樣的，第二題是在第一題的基礎上進一步深入探究，這兩題的第二問也都是新教材中增加的，這也表明教材設計者在知識點鞏固設計上的連續性和提高性，使學生的運算能力、思維能力得到進一步發展，讓學生形成良好的思維品質。

合作探究：

四、運用互補角求解高考題

2021 年新高考Ⅰ卷19 題：記△ABC的內角A，B，C的對邊分別為a，b，c。已知b2=ac，點D在邊AC上，BDsin ∠ABC=asinC。

（1）證明：BD=b；

（2）若AD=2DC，求cos ∠ABC。

本文探究的互補角主要包括三類：一是一個大的三角形分成兩個小的三角形后形成有公共邊的兩個互補角；二是平行四邊形中的互補角；三是圓內接四邊形中的對角互補。