基于UbD逆向視角的小學數學單元整體設計

曾競瑩

【摘要】學科核心素養是學科教育的歸宿，要求著單元教學整體化、連續化。強調逆向視角的UbD（Understanding by Design）教學設計方法恰好為單元整體教學提供了有效路徑。本文以人教版小學數學四年級上冊“除數是兩位數的除法”單元為例，按照UbD教學設計思路，注重從學習結果入手，整合零散的知識與技能，明確單元目標統領教學，設計評估方法檢驗學習，劃分單元課時確定任務，建構知識內容的框架，進而達成深度理解，實現應用遷移，發展核心素養。

【關鍵詞】小學數學;單元整合;UbD教學設計方法

【正文】

小學數學學科核心素養強調知識點從理解到應用，重視知識點之間的聯結及其運用。因此教學設計從一個課時變成單元整合已是必然，UbD教學設計模式為單元整合設計提供了有效路徑。UbD從字面上理解是理解為先的教學設計，從實質上理解則是一種以明確的學習目標為起點，強調以終為始的逆向思考，注重從學習結果入手，以促進學生有意義學習的教學設計模式。本文以人教版小學數學四年級上冊“除數是兩位數的除法”單元為例，按照UbD教學設計思路，整合零散的知識與技能，建構知識內容的框架，進而達成深度理解，實現應用遷移，發展核心素養。

一、單元目標統領核心教學

（一）單元前后概念梳理

小學階段的整數除法計算的整體知識結構從二年級下冊“表內除法（有余數的除法）”開始，到三年級下冊的“除數是一位數的除法”，最后到四年級上冊的“除數是兩位數的除法”，共分為3個階段。

本單元除數是兩位數的除法的計算原理與除數是一位數的除法相同，只是試商的難度加大，不僅和除數十位上的數有關，而且還和除數個位上的數有關，計算過程比較復雜，有時需要試商兩三次才能求出恰當的商，因此試商的方法是本單元的教學難點。

除此之外，除數是兩位數的除法計算是與之前的計算認知有區別的。在加法、減法、乘法豎式和除數是一位數的除法豎式，都是以計數單位拆分數再計算。比如計算268÷2，是將被除數拆分成“200+60+8”，再分別除以2。而本單元的除法計算需要將除數看成一個整體，不拆分計數單位，這是第一次出現，其實是算理問題，也是教學的難點。

（二）UbD單元目標確定

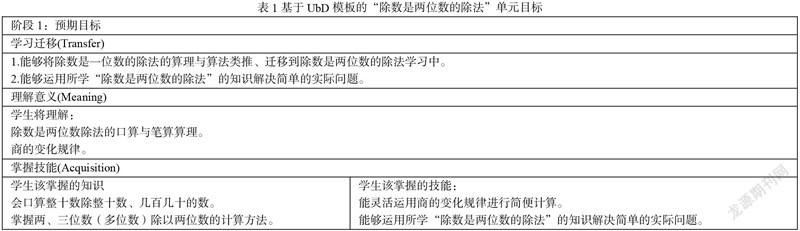
UbD教學模式的宗旨是理解為先，核心理念是讓學生了解學習目標，運用了逆向設計的原理。基于以上模式，在教學的第一階段，筆者充分了解小學數學課程標準、教材單元課時內容以及學生的已有經驗基礎，通過橫向多版本教材對比分析、縱向梳理教材內容安排，制定單元整合目標。如表1所示。

二、評估方法檢驗學習增量

UbD教學模式涉及的評估方法有：課堂交流評價、課后測驗、及自我評估等。如何確認學生己經達到相應的程度，教師需要對此做好相應的評估標準及時反饋。因此對于學生學習任務表現設置關鍵評估標準，保證評估的一致性與準確性。具體如下表所示：

三、單元課時確定目標任務

（一）單元學習序列活動安排

對比教材，人教版教材學習采用“口算除法——筆算除法（商一位數、商兩位數）——商的變化規律”的單元學習序列活動，北師大版教材采用“三位數除以兩位數——商不變規律——常見的數量關系”單元學習序列活動，并沒有按照“商的位數”編排，而是貫穿“定位—試商—調商”的思維主線設計例題，解決商是幾位數（定位）、如何試商（步驟和方法）、調商的重難點。這樣的整合使學生整體架構筆算除法，深化對筆算算理的理解，掌握筆算算法。

（二）學生現實經驗起點調查分析

筆者進行了一次教學前測，結果發現：學生口算計算的正確率為97.3%，每道題的正確率均超過了95%，表示除數是整十數的口算除法，學生有著較高的學習起點。但容易在計算過程中負遷移了“筆算乘法”處理因數末尾0的方法，會出現了“商在十位”，“商與除數的乘積寫成9”，“余數繼續除”等錯誤產生。另外，在實際教學過程中，筆者發現學生不會靈活運用試商方法，比如“同頭無除試商8、9”和“除數折半估商5”，試商也是一大難點。

（三）整體單元課時任務材料設計

【參考文獻】

[1]威金斯，麥克泰格.追求理解的教學設計[M].閆寒冰，宋雪蓮，賴平，譯.上海：華東師范大學出版社，2017.

[2]中華人民共和國教育部.義務教育數學課程標準（2011 年版）[M]. 北京：北京師范大學出版社，2012.

[3]崔允漷.學科核心素養呼喚大單元教學設計[J].上海教育科研，2019，（04），1.

[4]於青.基于UbD模式的教學設計與實踐——以異面直線所成角及其度量為例[J].中小學數學，2020，（7）.