基于直觀想象核心素養視角下多面體的外接球解題策略

陶昌熙

摘 要：近幾年高考（全國卷）對直觀想象核心素養的考查主要體現在立體幾何中空間想象能力的考查。其中多面體的外接球問題是高考數學試卷經常出現的題型，主要以選擇題形式呈現。如何解決此類問題是學生面臨的一道難關。本文將通過直接法、補形法、構造法，對如何處理多面體的外接球問題進行闡述。

關鍵詞：直接;補形;構造

多面體的外接球問題包含多面體和外接球兩個內容。高考題主要以兩類問題考查。學生應該掌握多面體的相關知識，以及外接球的知識。下面結合例子談談幾類多面體的外接球解題策略。

一、直接法

直接法即利用球的定義直接找出球心。直接找出球心的必備知識：球的定義。球就是在空間中與定點的距離等于定長的點的軌跡。此類問題關鍵是找到球心，那么如何找到球心呢？利用定性關系或定量計算找到一個定點到多面體各個頂點的距離相等，那么該定點就是球心;球心找到后再利用多面體的知識求出球的半徑。

二、補形法

補形法就是把球心不易找到的多面體補成長方體或直棱柱。學生可以利用長方體的球心在體對角線的中點上或者直棱柱的球心在上下兩個面的外接圓圓心連線的中點上找到球心。

三、構造法

構造法就是利用球心與截面圓心的連線垂直于截面的定理或者能夠找到兩條這樣的垂線就可以確定球心，然后構造直角梯形或直角三角形轉換成代數計算求出球的半徑。

（一）側棱相等但不互相垂直的棱錐

根據側棱相等可以證明頂點與底面外接圓圓心的連線垂直于底面。可以判斷球心一定在該垂線上。然后構造直角三角形轉換成代數關系，從而求出球的半徑。

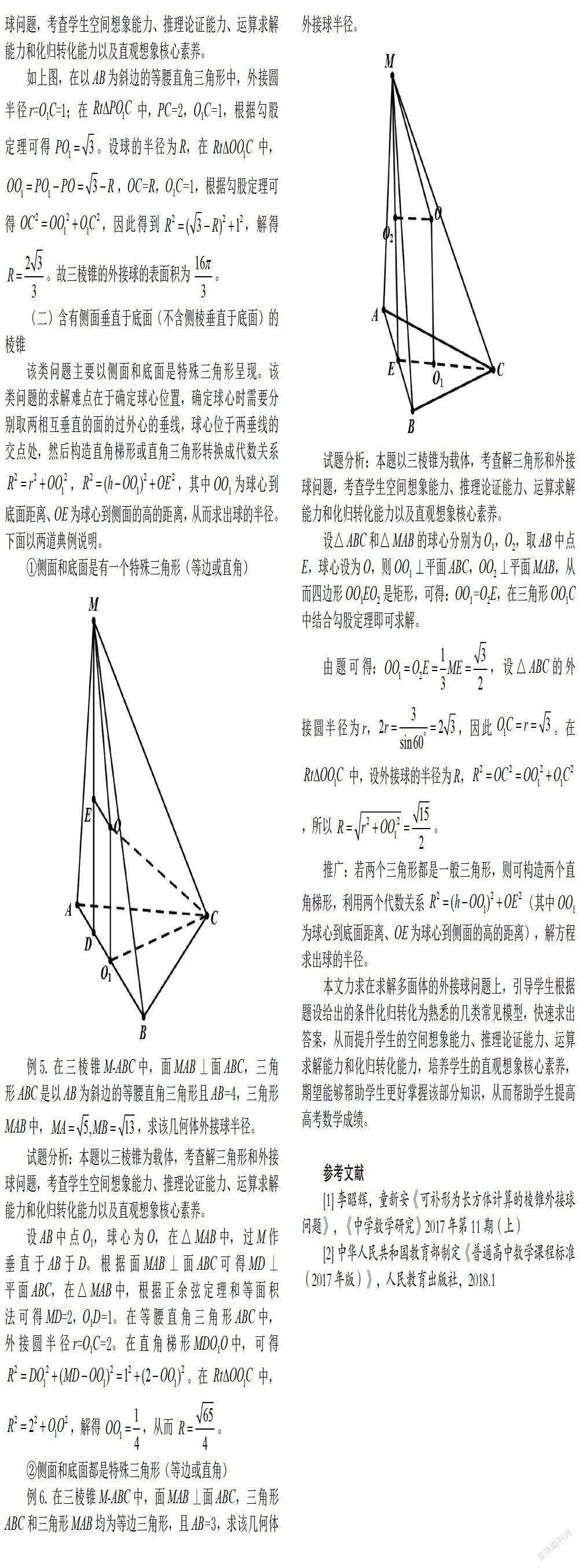
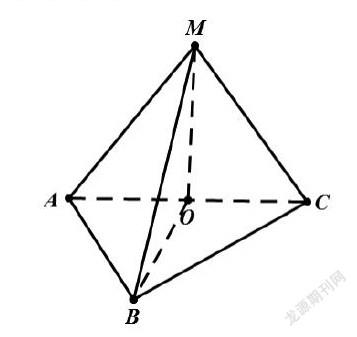
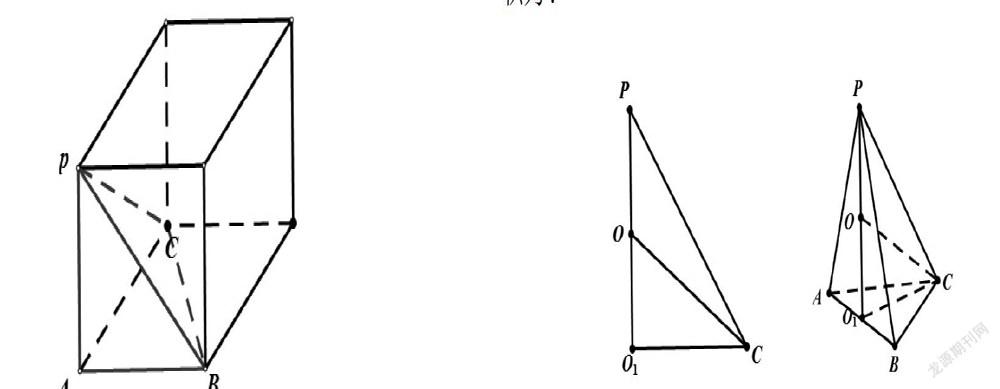
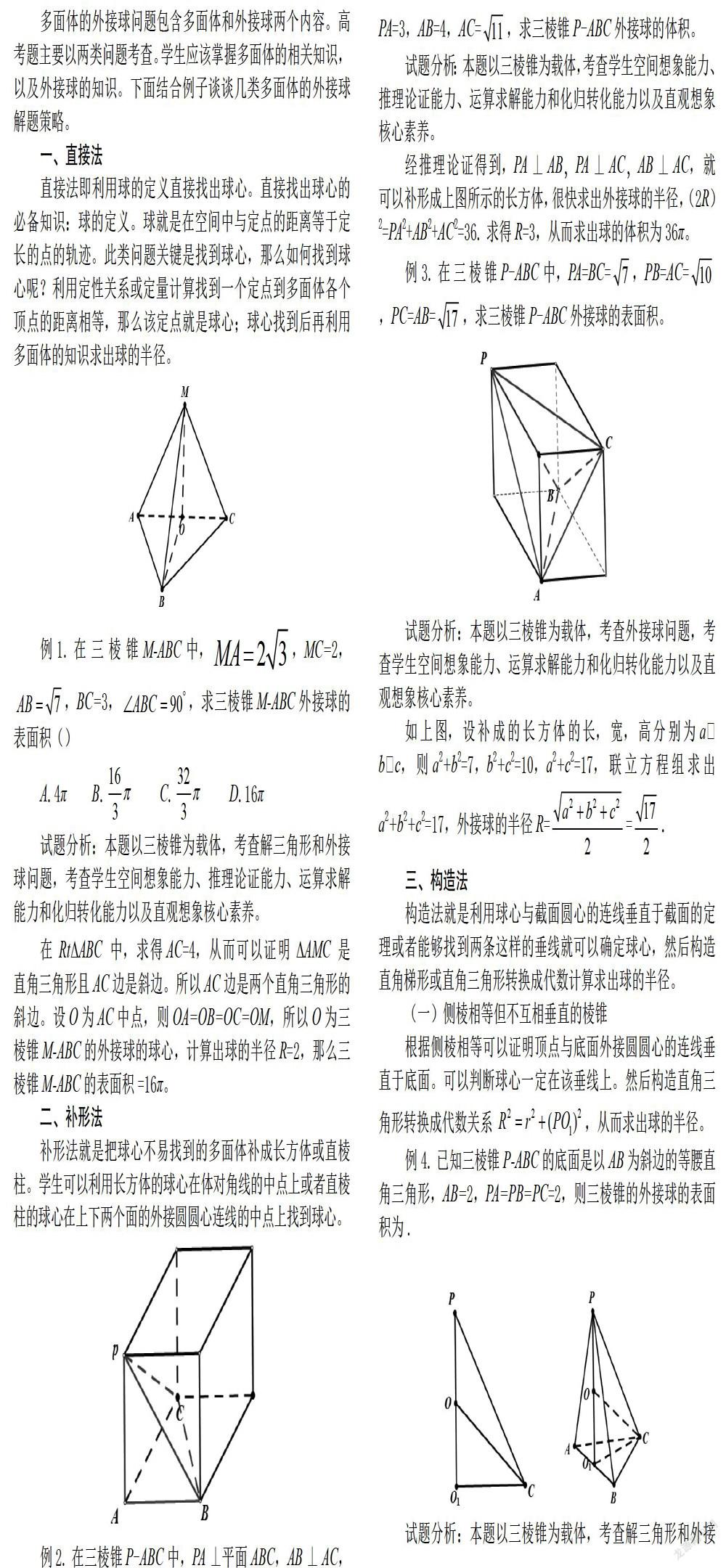
例4.已知三棱錐P-ABC的底面是以AB為斜邊的等腰直角三角形，AB=2，PA=PB=PC=2，則三棱錐的外接球的表面積為.

試題分析：本題以三棱錐為載體，考查解三角形和外接球問題，考查學生空間想象能力、推理論證能力、運算求解能力和化歸轉化能力以及直觀想象核心素養。

如上圖，在以AB為斜邊的等腰直角三角形中，外接圓半徑r=O1C=1;在中，PC=2，O1C=1，根據勾股定理可得。設球的半徑為R，在中，，OC=R，O1C=1，根據勾股定理可得，因此得到，解得。故三棱錐的外接球的表面積為。

（二）含有側面垂直于底面（不含側棱垂直于底面）的棱錐

該類問題主要以側面和底面是特殊三角形呈現。該類問題的求解難點在于確定球心位置，確定球心時需要分別取兩相互垂直的面的過外心的垂線，球心位于兩垂線的交點處，然后構造直角梯形或直角三角形轉換成代數關系，，其中OO1為球心到底面距離、OE為球心到側面的高的距離，從而求出球的半徑。下面以兩道典例說明。

①側面和底面是有一個特殊三角形（等邊或直角）

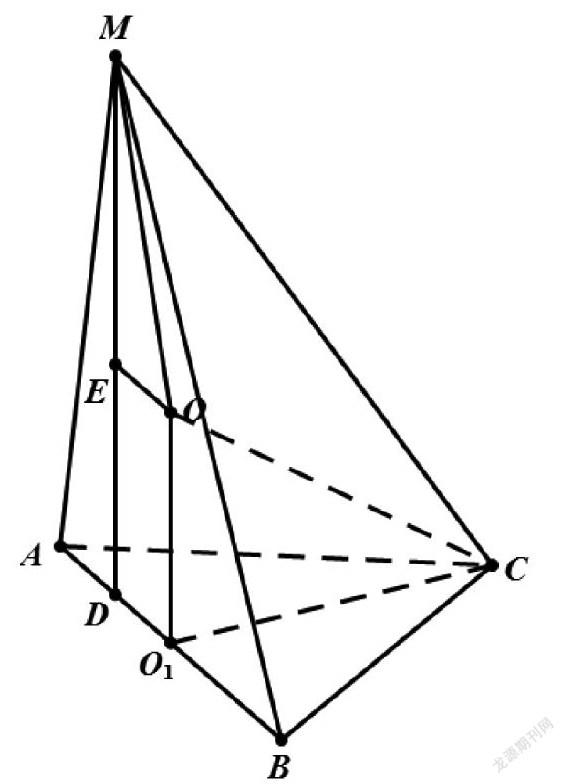
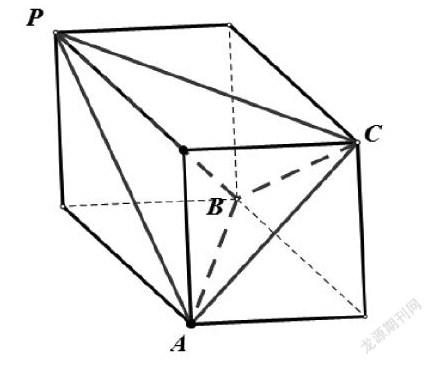
例5.在三棱錐M-ABC中，面MAB⊥面ABC，三角形ABC是以AB為斜邊的等腰直角三角形且AB=4，三角形MAB中，，求該幾何體外接球半徑。

試題分析：本題以三棱錐為載體，考查解三角形和外接球問題，考查學生空間想象能力、推理論證能力、運算求解能力和化歸轉化能力以及直觀想象核心素養。

設AB中點O1，球心為O，在△MAB中，過M作垂直于AB于D。根據面MAB⊥面ABC可得MD⊥平面ABC，在△MAB中，根據正余弦定理和等面積法可得MD=2，O1D=1。在等腰直角三角形ABC中，外接圓半徑r=O1C=2。在直角梯形MDO1O中，可得。在中，，解得，從而。

②側面和底面都是特殊三角形（等邊或直角）

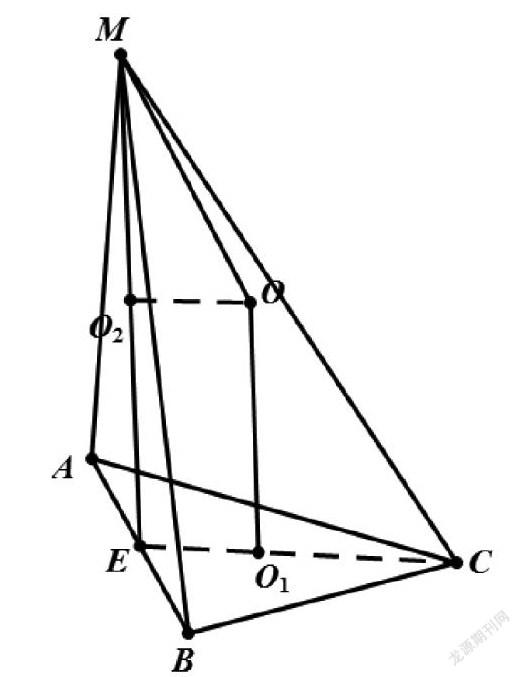
例6.在三棱錐M-ABC中，面MAB⊥面ABC，三角形ABC和三角形MAB均為等邊三角形，且AB=3，求該幾何體外接球半徑。

試題分析：本題以三棱錐為載體，考查解三角形和外接球問題，考查學生空間想象能力、推理論證能力、運算求解能力和化歸轉化能力以及直觀想象核心素養。

設△ABC和△MAB的球心分別為O1，O2，取AB中點E，球心設為O，則OO1⊥平面ABC，OO2⊥平面MAB，從而四邊形OO1EO2是矩形，可得：OO1=O2E，在三角形OO1C中結合勾股定理即可求解。

由題可得：，設△ABC的外接圓半徑為r，，因此。在中，設外接球的半徑為R，，所以。

推廣：若兩個三角形都是一般三角形，則可構造兩個直角梯形，利用兩個代數關系（其中OO1為球心到底面距離、OE為球心到側面的高的距離），解方程求出球的半徑。

本文力求在求解多面體的外接球問題上，引導學生根據題設給出的條件化歸轉化為熟悉的幾類常見模型，快速求出答案，從而提升學生的空間想象能力、推理論證能力、運算求解能力和化歸轉化能力，培養學生的直觀想象核心素養，期望能夠幫助學生更好掌握該部分知識，從而幫助學生提高高考數學成績。

參考文獻

[1]李昭輝，童新安《可補形為長方體計算的棱錐外接球問題》，《中學數學研究》2017年第11期（上）

[2]中華人民共和國教育部制定《普通高中數學課程標準（2017年版）》，人民教育出版社，2018.1