用心經(jīng)營 育好“復(fù)習(xí)林”

鄭漢成

摘要：復(fù)習(xí)課是小學(xué)數(shù)學(xué)教學(xué)中的重要課型之一，它是學(xué)生再現(xiàn)學(xué)習(xí)的一種手段。通過復(fù)習(xí)梳理，能喚醒學(xué)生已有的認(rèn)知與經(jīng)驗，將平時相對孤立地知識以再現(xiàn)、整理、歸納等辦法串聯(lián)起來，形成結(jié)構(gòu)嚴(yán)密的系統(tǒng)，進(jìn)而加深學(xué)生對知識的理解、溝通，讓學(xué)生在完善知識結(jié)構(gòu)的過程中溫故知新。人們常把新授課比成“種好一棵樹”，那復(fù)習(xí)課就要“育好一片林”。因此，教師要用心去組織，努力上好復(fù)習(xí)課，提升課堂有效性。

關(guān)鍵詞：復(fù)習(xí);知識核心;日記

一、回顧整理促活力

（一）自主梳理知識，構(gòu)建知識網(wǎng)絡(luò)

《數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》指出：某些單元知識，概念多，知識雜，各知識點表面看是零散的，實際上有著密切的聯(lián)系，通過復(fù)習(xí)整理，就能形成知識網(wǎng)絡(luò)。這類復(fù)習(xí)課可以利用思維導(dǎo)圖、知識樹、列表格等形式，學(xué)生親歷知識梳理、自主建構(gòu)的過程，培養(yǎng)學(xué)生創(chuàng)造性思維能力。

（二）回放過程方法，把握知識核心

在復(fù)習(xí)之前，學(xué)生的知識點和研究方法都以零散的形式存在于腦海中。復(fù)習(xí)不僅要把知識穿起來，形成一個整體，更要回顧探究的過程和探究時所用到的思想方法，使研究方法成為一個整體。

如五上數(shù)學(xué)“多邊形面積”的單元復(fù)習(xí)。我們要讓學(xué)生再現(xiàn)多邊形面積公式的推導(dǎo)過程，回顧在探究過程中用到了哪些思想方法。復(fù)習(xí)時，學(xué)生整理出三角形轉(zhuǎn)化成已學(xué)圖形的各種方法。有用兩個完全一樣的三角形進(jìn)行轉(zhuǎn)化，它們都可以拼擺成長方形或平行四邊形。有把一個三角形進(jìn)行轉(zhuǎn)化，可以通過剪拼、折疊、還原等多種方法轉(zhuǎn)化成長方形或平行四邊形。在此基礎(chǔ)上，再引導(dǎo)學(xué)生進(jìn)一步梳理各種轉(zhuǎn)化對應(yīng)的面積公式。

二、鞏固應(yīng)用提價值

（一）練習(xí)設(shè)計要有層次性

復(fù)習(xí)課的練習(xí)設(shè)計應(yīng)循序漸進(jìn)，逐步提高，有層次，有梯度。既給后進(jìn)生輔導(dǎo)性練習(xí)，又給優(yōu)秀生提高性練習(xí)，讓不同層次的學(xué)生都能有所獲。把由淺入深、層層遞進(jìn)的題安排在一起，讓學(xué)生的思考不斷深入，不斷提升，有利于學(xué)生把握問題的本質(zhì)，掌握同一類問題的共性。

如六上“圓的面積”復(fù)習(xí)課，為了鞏固圓的面積推導(dǎo)過程，我設(shè)計了這樣一組習(xí)題。

把一個圓平均分成若干等份，拼成一個近似長方形。

1.如果長方形的寬是1分米，求圓的面積。

2.如果長方形的長是9.42分米，求圓的面積。

3.如果長方形的周長比圓的周長長12分米，求圓的面積。

4.如果長方形的周長是16.56分米，求圓的面積。

通過以上4道題，層層深入，由易到難，前一題是后一題的基礎(chǔ)，后一題是前一題的延伸。尤其第4題學(xué)生不容易解決，但有1、2、3題的鋪墊，最終也會領(lǐng)略到“山重水復(fù)疑無路，柳暗花明又一村”的欣喜。

（二）練習(xí)設(shè)計要有開放性

復(fù)習(xí)題的內(nèi)容要不斷推陳出新，要輸入新鮮血液和養(yǎng)分。為了有效地檢測知識之間的聯(lián)系，需要設(shè)計一些開放性的習(xí)題。由于結(jié)果的多樣性和解題策略的不唯一性，為學(xué)生創(chuàng)設(shè)思考空間，培養(yǎng)了學(xué)生的創(chuàng)新精神。

（三）練習(xí)設(shè)計要有拓展性

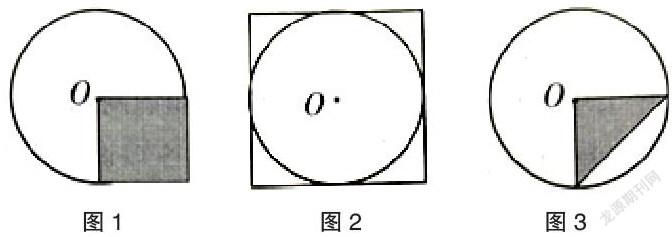
有時在題目中故意設(shè)置一些難度是有良苦用心的。如圖1，如果正方形的面積是5平方厘米，圓的面積是多少平方厘米？要解答這個問題，學(xué)生又遇到了新的問題。誰的平方等于5？思維阻塞時，迫使學(xué)生尋找別的出口。正方形的面積等于半徑的平方，也就是半徑的平方是5，那么圓的面積就是3.14×5，問題解決的巧妙而輕松。

“誰的平方等于5？”這個問題雖然沒有解答，但卻給學(xué)生打開了一片新的天地，今后遇到類似問題，也可以從尋找半徑的平方入手。

如圖2，圖中正方形的面積是20平方厘米，求圓的面積。圖3，三角形的面積是6平方厘米，求圓的面積。解決這兩題，也要緊扣半徑的平方，即找到一個小正方形的面積，問題就可以突破了。

三、撰寫日記拓情智

悉心指導(dǎo)學(xué)生撰寫數(shù)學(xué)日記，可以從以下幾方面寫：寫數(shù)學(xué)認(rèn)知、寫數(shù)學(xué)活動、寫數(shù)學(xué)思考、寫數(shù)學(xué)應(yīng)用、寫數(shù)學(xué)發(fā)現(xiàn)等等。學(xué)生的數(shù)學(xué)日記既有對所學(xué)知識的整理和總結(jié)，也有對課堂教學(xué)的理性思考，有對教師教學(xué)方式的探討，還有用所學(xué)知識編成數(shù)學(xué)童話。通過讓學(xué)生撰寫數(shù)學(xué)日記，給學(xué)生搭建了一個積累數(shù)學(xué)知識，豐富數(shù)學(xué)情感，拓展數(shù)學(xué)智慧，交流學(xué)習(xí)心得，溝通師生關(guān)系的平臺，不少學(xué)生通過與教師之間這種書面的交流，對數(shù)學(xué)教師有了親近感，學(xué)生學(xué)習(xí)數(shù)學(xué)成為一個愉快的過程，從而提高了數(shù)學(xué)學(xué)習(xí)成績。

參考文獻(xiàn)：

[1]韓兵.小學(xué)高年級數(shù)學(xué)復(fù)習(xí)課有效教學(xué)的三個途徑研究[J].課程教育研究，2019（22）.

[2]李啟龍.如何上好小學(xué)高年級的數(shù)學(xué)復(fù)習(xí)課見解[J].知識文庫，2019（23）.