基于多變量最小二乘法和粒子群優化的金團簇結構預測
孫悅 劉佳奇 侯冬雪 高闖

摘? 要:團簇科學是凝聚態物理領域中非常重要的研究方向,該文以金屬團簇金Au20為研究對象,利用999組已知的結構數據,運用最小二乘法通過最小化誤差的平方和尋找數據的最佳函數匹配簡便地求得未知的模型參數,進而建立金團簇Au20的Gupta能量預測模型。結合金團簇的能量預測模型,利用粒子群優化算法進行對原子結構進行優化,最終運用VMD軟件進行金團簇的全局最優結構重構,驗證模型的有效性和可行性。
關鍵詞:原子團簇? ?結構優化? ?Gupta勢能函數? ?粒子群算法
中圖分類號:TB383.1? ? ? ? ? ? ? ? ? ? ? 文獻標識碼:A文章編號:1672-3791(2021)06(c)-0188-04
Structure Prediction of Gold Clusters Based on Multivariable Least Square Method and Particle Swarm Optimization
SUN Yue? ?LIU Jiaqi? ?HOU Dongxue? GAO Chuang*
(School of Electronic and Information Engineering, University of Science and Technology Liaoning, Anshan, Liaoning Province, 114051? China)
Abstract: Cluster science is a very important research direction in the field of condensed matter physics. This paper takes Metal Cluster Gold Au20 as the research object, uses 999 groups of known structural data, uses the least square method to find the best function matching of the data by minimizing the sum of squares of errors, easily obtains the unknown model parameters, and then establishes the Gupta energy prediction model of gold cluster Au20. Combined with the energy prediction model of gold clusters, particle swarm optimization algorithm is used to optimize the atomic structure. Finally, VMD software is used to reconstruct the global optimal structure of gold clusters to verify the effectiveness and feasibility of the model.
Key Words: Atomic clusters; Structure optimization; Gupta potential energy function; Particle swarm optimization
團簇研究正在迅猛發展,是跨越原子、分子物理、固體物理、表面物理、量子化學等諸多學科的一個交叉學科。但由于團簇的勢能曲面上存在著大量的局部極值,同時需要考慮相對論效應等,所以要想找到團簇的全局最優結構是十分困難的。傳統的計算方法中隨著原子數的增加,高精度的理論計算時間呈現指數型增長,耗時嚴重。所以,團簇能量預測模型的研究在很多方面還需要不斷完善。基于慣性權值非線性遞減的改進粒子群算法或結合自適應免疫優化算法和動態格點搜索操作以及無偏優化算法優化了團簇的最穩定結構,具有較高的計算速度和成功率,但需要指出的是團簇的初始構型是隨機生成的,內部操作也有一定的隨機性,因此應對該方法進行進一步的改進[1-3]。基于CALYPSO結構預測方法和密度泛函理論的第一性原理、粒子群優化算法,結合隨機學習、競爭機制以及變異算子、多種經典啟發式算法、動態格點搜索算法以及遺傳算法結合密度泛函TPSS對勢能面提出了一些高效的、無偏的優化算法[4-8]。與上述文獻的建模方法不同,該文采用多變量最小二乘法和粒子群優化算法,通過智能方法建立金團簇的能量預測模型,并利用該模型找到金團簇的最優原子結構,最后通過VMD軟件對原子結構進行重構,進行穩定性分析,驗證所提出模型有效性。
1? 模型的建立與求解
1.1 數據預處理
選取999組金團簇Au20的結構異構體數據,利用MATLAB軟件進行數據預處理,具體步驟如下。
Step 1:將每組的三列數據放至一列,設置兩個變量n1,n2,分別從0~99,100~154,156~199,200~299,300~399,400~499,500~599,600~699,700~799,800~899,900~999對其賦值,共11組。
Step 2:利用for循環和num2str函數先將i變量轉換為字符型。
Step 3:用textread函數對數據進行讀取得到A1 cell文件,后用str2num函數將其轉換為double型進而得到向量m。
Step 4:設置一個空矩陣B,將m中的一列數據分為每列61行存放在矩陣A中,將A賦值給B,得到最終處理好的數據。
Step 5:重復Step2~4,完成全部11組數據的預處理,得到999列的建模數據B。
1.2 基于多變量最小二乘法的Gupta能量預測模型
為了建立金團簇的Gupta能量預測模型,基于999組實際數據,可采用多變量最小二乘法回歸出金團簇的勢能預測模型。Gupta勢函數可描述金團簇中金原子之間的相互作用。Gupta勢函數可以分解為斥力項Vr(i)和引力項Vm(i),對于原子總數為N的團簇勢能函數Vn表述為[1]:
(1)
(2)
其中,N為團簇原子總數;rij代表原子i和j之間的距離;rij是最近鄰近平衡距離;Aij是斥力項系數;ξij代表原子i和j之間的有效跳躍積分參數;pij和qij分別描述為對斥力與引力作用的權重。
上述模型中的除了N和rij的其他5個參數可采用多變量最小二乘法,結合999組數據,對參數進行辨識,最小二乘法是一種常用的數學優化方法,它通過最小化誤差的平方和尋找數據的最佳函數匹配。它可以用于函數曲線擬合。在無約束最優問題中,其目標函數可表示為:
(3)
其中,Li(x)是x的非線性函數,該題的Li(x)選擇為Gupta勢函數。具體建模步驟如下。
Step 1:讀取999組實際數據,設定5個待辨識參數的初值。
Step 2:根據數據中的坐標信息,計算出各個原子之間的距離rij。
Step 3:在MATLAB中調用最小二乘lsqcurvefit函數,將初值和距離rij代入函數中進行計算。
Step 4:通過lsqcurvefit函數的返回值Cof,得到辨識后的5個參數實際值。完成金團簇的Gupta能量預測模型建模。
1.3 基于粒子群算法的金團簇結構優化模型
建立Gupta能量預測模型后,可利用粒子群優化算法對各原子之間的距離進行優化,得到勢能更低的金團簇結構異構體。該算法具有獨特的搜索機制,是受鳥群捕食行為的啟發而提出來的一種群體智能優化算法,其數學描述為:設在一個D維搜索空間中,每個粒子是一個點,粒子規模為N,第i個粒子的位置矢量可以描述為xi=(xi1,xi2,…,xid),速度矢量可描述為vi=(vi1,vi2,…,vid),第i個粒子搜索到的最優位置為pi=(pi1,pi2,…,pid),稱為個體極值,表示粒子的個體經驗;整個種群搜索到的最優位置為pg=(pg1,pg2,…,pgd),稱為全局極值,表示粒子的群體經驗[4]。粒子的速度和位置更新公式如下:
(4)
式中,w為慣性權重;k為當前迭代次數;C1和C2為加速因子,是非負的常數;r1和r2是分布在[0,1]之間的隨機數。
利用上述公式,可完成金團簇原子距離的優化,具體建模步驟如下。
Step 1:初始化種群數量、迭代次數以及原子數量等粒子群參數。
Step 2:隨機生成初始種群(原子坐標)的初始解,將初始解代入Gupta勢函數(1)和(2)中,計算出各個勢能值。
Step 3:根據當前的最優解,利用式(4)的更新規則求出種群下次迭代的位置。
Step 4:重復Step 2和3,達到最大迭代次數時,得到最優解,即為本次運行的全局最優解,其對應的20個原子坐標組成的金團簇是全局最優結構。
2? 結果檢驗
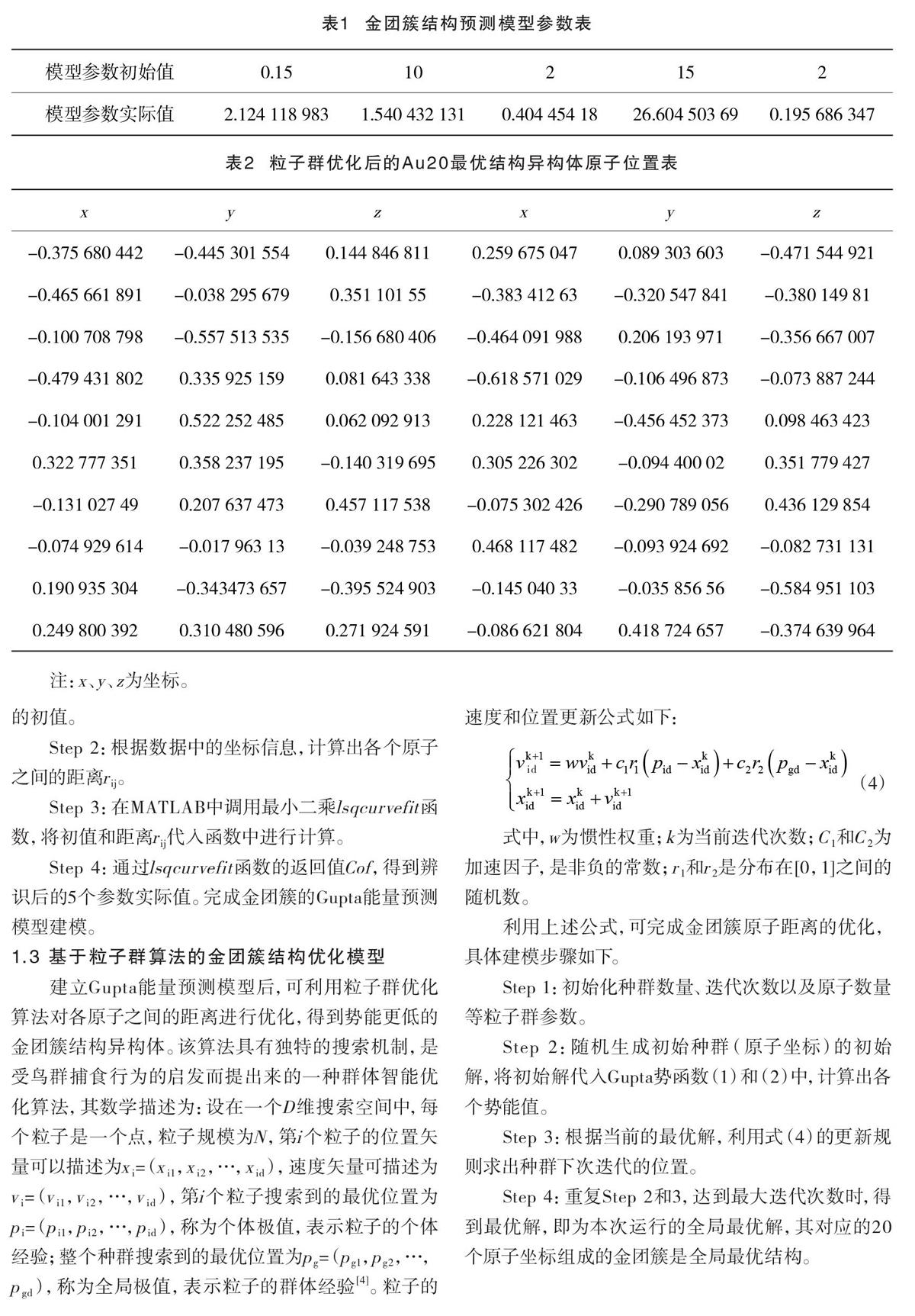
根據1.3的建模步驟,利用MATLAB軟件進行仿真,可建立金團簇結構預測模型。模型的初始值和實際值見表1。
根據1.3的建模步驟,設置PSO的種群數量為50,迭代次數為2 000,可找到金團簇Au20的全局最優結構,最優結構的原子坐標信息見表2。
Au20的全局最優結構見圖1,從圖中可以看出,四面體結構的Au20納米團簇具有配體保護的金納米團簇中的熒光將團簇聚集源與定制的離子光學和大量選擇過程相結合,創造出了一束裸Au20簇,然后把它們植入固體氖基質中。它們是通過沉積具有氖背景氣的團粒束獲得的,然而氖氣是一種惰性氣體,與其他物質相互作用較弱。氖中固有的結構和光學團簇性質在實驗中能夠得以保留,因此穩定。
3? 結語
該文利用多變量最小二乘法,可以更簡便地獲取模型所需參數,提高了模型的預測效率;Gupta模型的適用范圍很廣,能夠允許除該文所用的數據進行能量預測,進而找到可能存在的最優化結構,體現了模型的實用性和合理性。后續工作,可采用更高效的元啟發式優化算法替代,可獲得更準確的模型參數;粒子群算法的程序里較大,算法復雜,可采用更簡便的優化算法替換,例如鯨魚群優化算法等,優化策略更簡單高效。
參考文獻
[1] 吳夏,董彥杰.Gupta與Sutton-Chen勢函數的金團簇穩定結構[J].計算機與應用化學,2014,31(11):
1333-1336.
[2] 周營成.基于群智能和機器學習的新型納米團簇結構預測研究[D].北京:北京化工大學,2020.
[3] 宋婉婷,孫彤,張如杰,等.Au_mY_n(m+n≤6)團簇的結構、穩定性及電子特性研究[J].分子科學學報,2019,35(6):503-508.
[4] 華勇,王雙園,白國振,等.基于慣性權值非線性遞減的改進粒子群算法[J].重慶工商大學學報:自然科學版,2021,38(2):1-9.
[5] 周營成.基于群智能和機器學習的新型納米團簇結構預測研究[D].北京:北京化工大學,2020.
[6] 熊荊武.預測Au團簇基態結構的啟發式優化算法[D].武漢:華中科技大學,2017.
[7] 汪光煉.預測Au團簇基態結構的動態格點搜索算法[D].武漢:華中科技大學,2015.
[8] 田志美.配體保護金團簇的結構預測及電子結構分析[D].合肥:安徽大學,2018.

