基于PSO算法優化BP神經網絡的金融風險防范預警模型研究

吳川惠 王昭

（西安歐亞學院，陜西 西安 710065）

傳統的BP神經網絡模型豐富了金融風險預警模型體系，能夠實現從輸入到輸出過程復雜非線性的映射，具有很強的學習能力，但BP神經網絡算法易陷入局部最優解，而隨機的初始化權值和閾值使其出現每次訓練的結果都不一致的情況。本文將利用種群中個體對信息共享的特征，可以自適應地調整搜索方向，以便具備隱行性和全局尋優能力的粒子群優化算法（PSO）對BP神經網絡的權值和閾值進行優化，以此解決BP神經網絡存在的局部收斂性問題，從而動態地在海量數據中提取隱藏規律，提高對經濟指標的全局搜索和預測能力。

一、金融風險防范預警指標體系

金融風險預警模型防范金融風險，需要通過實時地監測金融指標的動態變化來實現，所以指標體系的構建需要具有時效性、靈敏性、可操作性以及系統性等特點。通過借鑒國內外相關文獻和訪談相關專家，確定了三大類風險為金融監管風險、金融機構風險以及證券保險國際收支的交叉類風險。本文以科學性和有效性原則，構建了與金融風險預測相適應的預警指標體系，涉及9類具體風險類型和24個變量指標。根據上述各大類風險中具體風險的變量指標，選取2010—2019年我國相關金融數據作為樣本（見表1），用以檢驗預警模型的金融風險預測效果。

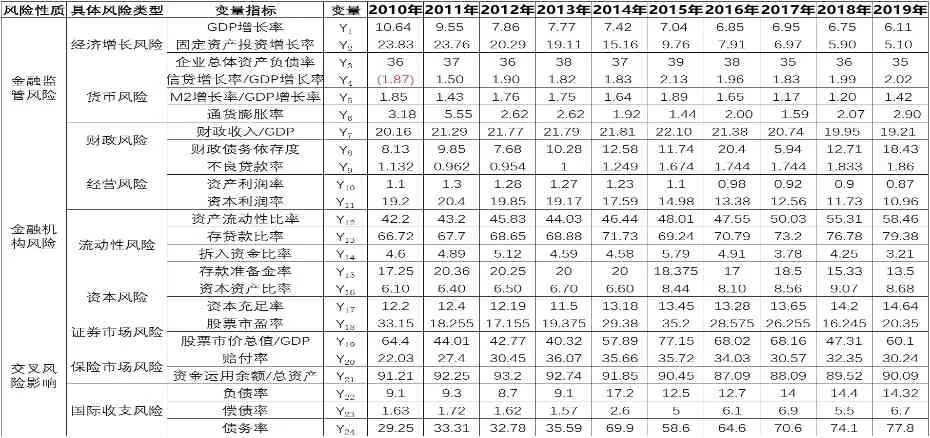
表1 金融風險防范預警指標體系

二、金融風險防范預警模型構建

針對BP神經網絡具有收斂速度慢、易陷入局部極值點、學習過程易發生振蕩和訓練時學習新樣本過程中有遺漏舊樣本等問題。本文將PSO算法對BP神經網絡的權值和閾值進行優化，以解決這些問題。基于PSO優化的BP神經網絡主要流程如下：

Step1：設定神經網絡的輸入層節點數、隱層節點數和輸出層節點數以確定BP神經網絡拓撲結構，確定神經網絡的權值和閾值的函數分量，以方便后續調用優化。

Step2：初始化粒子群的速度、最大迭代次數、學習因子、種群規模和粒子位置。

Step3：通過網絡訓練，計算粒子的適應度函數值，得到粒子個體最優解和全局最優解，通過比較，記錄粒子種群的最優位置。

Step4：重新調整當前粒子的速度和位置，將新個體插入到種群中，當訓練網絡的誤差滿足設定條件時，則終止迭代，計算并得到結果，否則轉步驟3，繼續迭代直至算法收斂。

Step5：將PSO優化的權值和閾值賦予BP神經網絡的初始權值和閾值，獲取優化后的BP神經網絡結構，從而反復迭代完成訓練，輸出預測值。

三、金融風險防范預警模型實證檢驗

為了驗證構建的金融風險防范預警模型可行性，本文采用Matlab2016a軟件對金融風險防范預警模型進行訓練和檢驗。

（一）粒子群算法預置參數

根據經驗值進行設置，種群大小個數為300，最大速率0.01，適應度閾值0.000001，學習因子c1 = 2、c2 = 0.8，迭代次數n為500，粒子位置Xmax＝1，Xm i n＝－1，粒子的速度Vmax＝1，Vm i n＝－1，粒子的慣性權重w 采用線性遞減方式其中Wmax=0.9，Wmin=0.3。

（二）BP神經網絡預置參數

整個網絡由3層構成，輸入層節點數為9，主要輸入2010年至2018年的24個指標的數據，輸出層值為2019年度的預警指標數據，隱層節點數根據經驗不斷地進行網絡訓練，確定隱含層節點數為9時，誤差較小且效果最優。傳遞函數Sigmoid，訓練次數為1000次，訓練目標是0.000001。

（三）模型評價指標

為了便于更加準確地評估金融風險防范預測模型的準確性，本文選用了2個評價指標，分別為平均絕對誤差（MAE）和平均絕對百分誤差（MAPE）。

（四）適應度曲線

在迭代進化過程中，前期減幅較大，而后平均適應度曲線總體下降趨勢減緩，當迭代次數達到500時，適應度曲線逐漸趨于平緩（見圖1）。

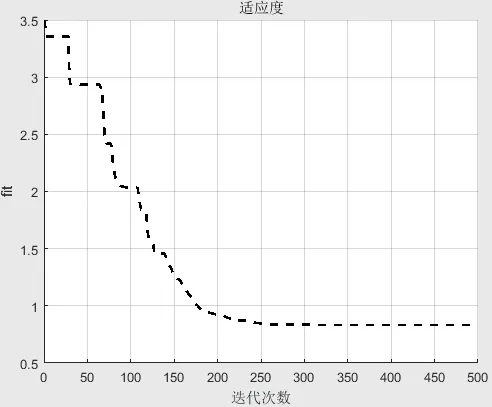
圖1 適應度曲線

（五）優化的神經網絡權值及閾值

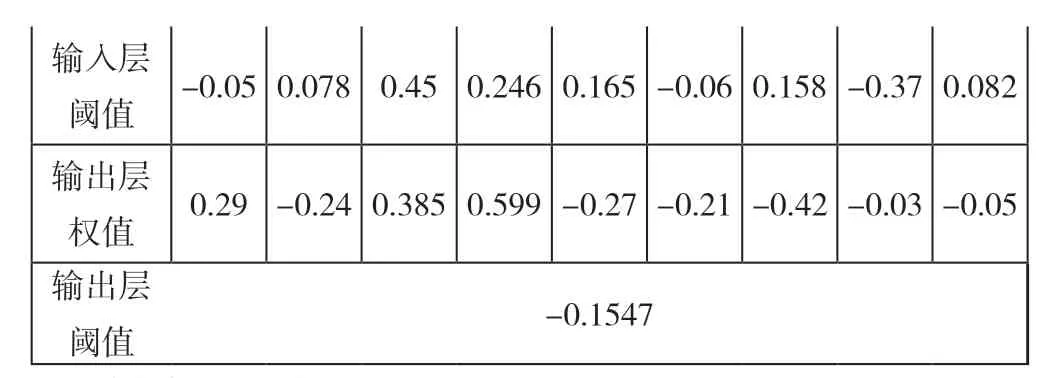
迭代完成后，找到最優粒子，得到PSO優化的權值和閾值（見表2），將其最優粒子的位置向量值賦給BP神經網絡的權值和閾值，使得BP神經網絡性能達到最優。

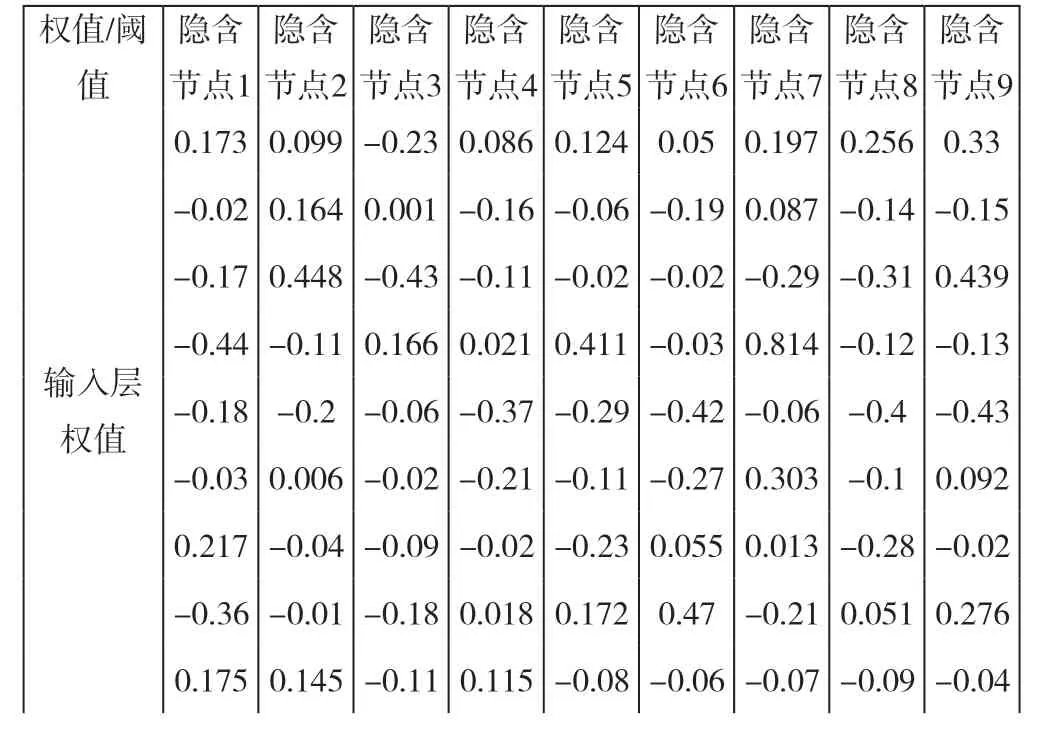
表2 PSO算法優化BP神經網絡的最優權值和閾值

?

（六）預測結果分析

由圖2預測真實值可以看出PSO－BP神經網絡模型的預測值與實測值非常接近，其中最大相對誤差為1.5%，最大絕對誤差為3.6，誤差在可接受范圍內，表明此算法性能較好，因此可以將預測結果用于模擬計算。

圖2 預測真實值

四、結束語

運用PSO算法優化的BP神經網絡模型進行數據處理，在對我國金融風險動態預測中，模型會自動吸取歷年各個指標的歷史變化趨勢，挖掘出潛在可能存在的風險信息，比較準確的預測出期望年度各指標的數據，然后再與國家監管部門的風險閾值自動對比，形成風險地圖，使得政府部門的干預措施具有戰略性。構建金融風險防范預警模型，并以此為基礎構建我國的金融風險監管體系，通過以上實證數據的檢驗具有可行性，推進了我國實施整個金融風險防范預警體系的信心。