培問題之“壤” 長思維之“花”

施李丹 姚海燕

[摘 要]針對小學低段學生提問中的“問題思考不敏銳”“問題呈現不主動”“問題表述不清楚”等現狀，主張實施“思·現·煉”策略，即根據小學低段學生的認知特點和思維特點，引導學生精準化思考問題，將問題緊扣數學本質;再鼓勵學生主動地呈現問題，凸顯困惑思路;最后提升學生的語言思維。以估測習題教學為例，談如何利用“思·現·煉”策略培養學生發現和提出問題的能力，提升學生的思維水平。

[關鍵詞]估測;習題教學;思維能力

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）29-0016-04

【課堂回顧】

教學片段1：給予參照物表象，首次思考估測問題

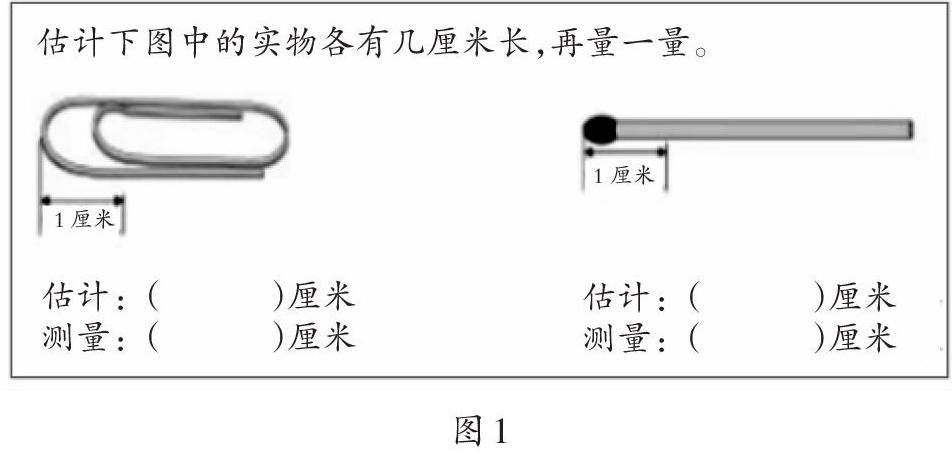
出示人教版教材二年級上冊“長度單位”單元練習一的第1題：

1.引導學生思考“什么是估”

師：仔細讀題，有不理解的地方嗎？

生1：這個“估計”是什么意思？

師：哪位同學知道？

生2：我認為估計就是大概的意思。

生3：我感覺估計的話不用真的去測。

師：確實，估計長度就是大概多長的意思，如果只是要知道估計的數據，我們是不用進行測量的。既然理解了估計的意思，就請獨立解決問題。

2.引導學生思考“怎么估才準”

（1）正誤辨析，初構問題

師：在解決問題的過程中遇到什么問題嗎？

（學生沒有反饋）

出示（學生估計的答案）：2厘米、3厘米、4厘米、10厘米。

師：大家覺得哪個估得準？

生4：3厘米，因為我測量出來的也是3厘米。

師：這位同學沒有測量就估出3厘米，確實厲害！其他同學會感到困惑嗎？

生5：為什么估3厘米？而不是1厘米、2厘米……

師：你認為3厘米怎樣？

生5：很準。

師：所以你想問的是？

生5：怎么估才能更準一些呢？

師：非常了不起的問題，你這個問題在解決估測問題上是非常重要的！接下來我們就一起探究怎么估。

（2）展露隱思，探尋估法

師：有位小朋友給“1厘米”標了“？”（如圖2），現在就請她來說說感到疑惑的問題。

生6：這個是干什么的？

師：不要緊張，試著讓大家都明白你要表達的意思。

生6：就是為什么要1厘米……

（教師再三鼓勵，生6還是說不下去）

師：誰來幫他把問題說清楚、說完整？

生7：我覺得他是想問“為什么標1厘米，而不是標其他的長度？”。

生8：他想問1厘米是不是能幫助我們估計？

生9：1厘米在這里到底有什么用？

師：你們都很厲害，不僅能互幫互助，還能想出這么了不起的問題。大家記得在哪里接觸過和“估”有關的題嗎？

生10：上學期學過估數，幾個十。

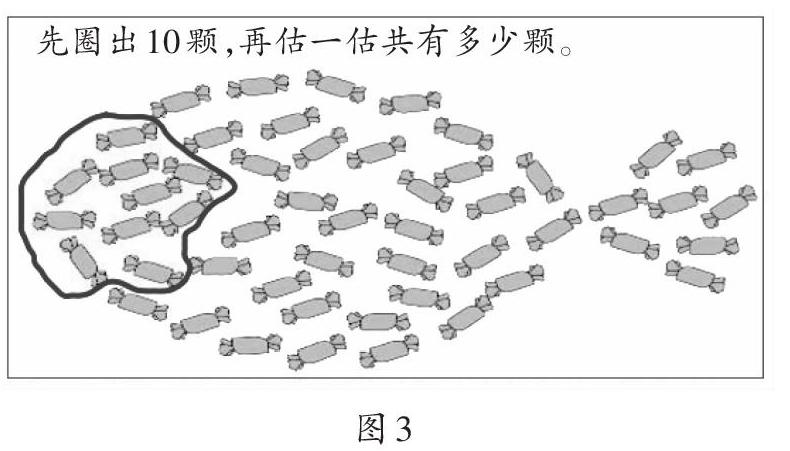
師（出示題目）：你的記性真好，還記得當時是怎么估的嗎？

生11：先知道10顆有多少，然后看這一堆里大概有幾個10顆就可以估作幾十。

師：和我們今天這道題目有什么聯系？

生12：一樣的道理，1厘米和10顆都是用來幫助我們估計的，看回形針大概有幾個1厘米就是幾厘米。

師：確實，“10顆”“1厘米”就是起到參考的作用，是參照物。不管什么物體，只要找到參照物，觀察這個物體有幾個參照物的大小就能估得準，如果一開始估的方法不對的再來試一試吧！

教學片段2：抽離參照物表象，深度思考估測問題

出示數學課堂作業本第2頁第2題：

1.聚焦沖突，再探估法

（1）自構表象1厘米：估測時未出示“1厘米”也可估

生1：這一題怎么估呀？

師：我們不是學過怎么估了嗎？你的問題是什么？

生1：這一題沒有1厘米了，怎么估？

生2：1厘米多長難道你不知道？

師：知道1厘米多長確實很重要，無論1厘米是否出示，心里都要有它。

（2）靈活拓寬參照物：估測參照物并非只有“1厘米”

生3：可是腰身呢？

師：慢慢來，把話說清楚、說完整，腰身怎么了？

生3：一拃長可以估計，因為看自己的手就能想象有幾個1厘米，但腰的話就要加幾十個1厘米，太麻煩了，怎么估？

師：這個問題確實是傷腦筋。怎么估才能不麻煩？

生4：參照物可以是一拃呀，我一拃是12厘米，量得5拃，估計是60厘米。

生5：把10厘米當作參照物也可以，用手大概量出10厘米后去圍著腰身量一圈，看大概有幾個10厘米就是幾十厘米。

師：你們的方法都可行，而且你們都在述說一個道理：估測時為了方便可以尋找一個合適的參照物。

2.題后遠思，再度提問

（1）對比生疑，聯系生活

師：會估會測量了，那對于“估和測量”還有什么想問的？

生1：為什么又估又量？直接量不就好了？

生2：什么時候需要量，什么時候可以估？

師：都是好問題！那誰能舉例說說什么時候需要量，什么時候可以估？

生3：如果我爸爸想戴我的手套，我就可以估計他戴不了，因為他的手太大了。

生4：如果我的手套壞了，媽媽想給我織新的手套就要量我手掌的大小。

師：同學們很擅于聯系生活思考問題。確實，估和量在生活中有不同作用，能估計時用估更方便，但需要精確數值時就得量，避免出現差錯。

（2）舉一反三，延續思考

師：到現在為止，我們學了估數、估測，你還有什么想問或者想說的嗎？

生5：除了估數、估測，還有什么也可以用“估”來解決？

生6：是不是還可以估大??？

師：你們已經會舉一反三地思考問題了，真棒！今后我們還會學習和“估”有關的內容，所以留個懸念給大家，大家也可以自己去發現……

【課后反思】

教學片段1中，學生對于“估測”的學習屬于首次，由于生活經驗不豐富，學生對于“估”存在較多問題。教學片段2是學生學完估測后的課堂練習，雖然學生解決過“什么是估”和“怎么估”，但因為習題脫離了參照物，學生的思維再一次受阻，出現問題較多。低段學生對問題的感知不敏銳，問題呈現不主動，在提問時表達過于籠統或不清晰。因此，筆者在常態課上就會注重培養學生發現和提出問題的能力，通過引導學生精準思考問題、鼓勵學生主動呈現問題、指導學生清晰表述問題來發展學生的思維能力。

一、逐引問思，提升學生的思維水平

教學時先引導學生思考問題從視點走入質點，最終帶領學生思考發展的遠點。所謂視點，即信息切入口;質點，即數學知識、方法上的核心點;遠點，即質點之后可引領學生抵達的高度，即由數學知識延伸至生活或由一及類。

1.視點切入，基于文本理解的問題思考

在與文本對話中往往需要主動對接原有的生活經驗和數學經驗，而低段學生的感知能力較弱，理解詞句的能力比較弱， 因此，促進低段學生思考問題可從文本信息切入，通過文本閱讀自我診斷，從中發現問題。這同時也能考查學生是否帶著思考在審題。

教學片段1中，筆者讓學生閱讀文本信息，生活經驗不豐富、詞匯量不足的學生的思維馬上聚焦在了“估計”一詞上，他們會提出問題“什么是估計？”。通過“估”的切入，學生理解了“估”的意思，才能繼續思考更本質的內容，避免后續階段的無效投入。

2.質點深入，基于本質探尋的問題思考

弗賴登塔爾曾說：“學習數學的唯一正確的方法是實行‘再創造，也就是由學生本人把要學的東西，自己去發現和創造出來?！睘榇?，在知識的本質處、核心處要引導學生自己生發問題，引發學生深度思考，使學生的探尋能有效指向知識的本質。

理解“估”不是重點，“會估”才是本質。在教學片段1中，學生未意識到自己的問題時，筆者通過“正誤辨析”“聚焦沖突”“對比生疑”“舉一反三”等策略給予學生思考問題的方向，逐步引導學生思考核心問題“怎么估”。而在探究核心問題過程中，筆者引導學生提出一個個問題：“1厘米有什么用？”“沒有1厘米了怎么估？”“腰身用1厘米不好估怎么辦？”……以小問題的解決最終解決大問題。

3.遠點延伸，基于外延聯想的問題思考

數學學習既要知內涵，又要知外延。除了從知識的核心處去思考問題，還要讓學生感受知識的價值。教師是學生思維生長的助推手，解決完問題并不代表學習結束。

教學片段2中，“會估會測量了，那對于‘估和測量還有什么想問的？”就是在學生理解了估意、估法后，筆者引導學生對比“估”和“測”。學生提出的問題“為什么又估又量？直接量不就好了？”“什么時候需要量，什么時候可以估？”雖然不作為學習要求，但筆者希望學生學數學的同時也會用數學，因此讓學生思考并觀察生活。此外，筆者引導學生通過舉一反三來思考問題“還可以用估來解決什么？”“是不是還可以估大?。俊薄紤]到教學要為下一次學習留住生長點，筆者沒有解說答案，因為問題不一定必須得解決，學生發現并提出問題的過程就能促進他們思維生長。

二、外顯問意，滿足學生的心理需求

低段學生正值喜歡提問的年紀，但教師在課堂上經常感受不到，原因有二：一方面，學生因害怕提錯問題而不敢問;另一方面，一節課只有40分鐘，教師不可能時時等待學生提出問題。因此，在“育問”路上教師要感同身受不同學生的處境，滿足不同學生的心理需求，讓學生養成主動提問的習慣。

1.靜待花開，給予提問能力弱的學生思考問題的機會

學生認知發展水平的不同，導致他們感悟問題的時間也有所不同，提問能力弱的學生往往需要較長的時間才能感悟到自己的問題。數學教學應最大程度地開啟每個學生的智慧潛能。當學生處于思考問題的環節，筆者均會留出一定的思考時間。對于提前發現問題的學生，筆者要求他們以“疑問手勢”（如圖6）示意，避免脫口而出的問題打斷其他學生的思考，待較多學生發現問題后筆者再指名學生提問。

2.以退為進，呵護膽小學生思考問題的意識

在看似熱鬧的課堂之下，潛藏著很多“沉默的疑惑”，一些生性膽小的學生不擅長展示自己的內心活動，也就得不到教師點撥的機會。筆者不強求這些學生必須提問，而是鼓勵他們在探究過程中思維受阻時可以圈圈畫畫，或標智慧符號“？”，筆者就能通過這些符號及時關注到他們的內心需求。

在教學片段1中，給“1厘米”標了“？”的學生的成績不是很好，他性格也較為內向，基本不敢舉手提問?！?厘米的作用”屬于探究估測法的必經之路，聰明的學生也許根本不會想到這個問題，但對于學困生而言，發現這個問題時就表明思維在生長，因此，教師要給予他們關注和鼓勵，讓他們的問題意識得到充分呵護。

3.見縫插針，展露學生思維生長的節點

在整個課堂教學中教師要以學生為主體，致力于培養學生在學習過程中的自主性和參與性，提高學生的表現力。因此，筆者允許學生在任何時候發現數學問題，但沒有提問機會時，可以高高舉起“智慧”手勢，避免學生的真問題由于沒機會提問而流失。

教學片段2中一句“可是腰身呢？”屬于學生真實存在且迫切想解決的問題，在課堂如常進行之時，“可是腰身呢？”這個問題再一次點燃了集體的思維火花，帶給了提問者成功的體驗。學生經歷了“用1厘米為參照物來估→去掉1厘米后靠想象來估→非1厘米為參照物來估”的思維過程，這個過程將估測的方法展現得淋漓盡致。

三、培育問語，發展學生的語言思維

“能用語言組織表達出來，是對認知的一種證明。思維在沒有被表達出來前是一團無形的東西，語言將思維表達出來后，思維就變成了有意義的信息。”低段學生的語言表達能力往往還不成熟，教師要有針對性地培養，使得學生在表達問題的過程中獲得新的思考路徑，促進語言思維的提高。

1.表達卡點時，及時點撥

提問開始階段，學生的思維會呈現無序狀態，學生表述時會詞不達意，作為課堂中的引導者，教師應該幫助學生將無序思維變得有序，混亂的語言變得清晰。在教學片段1中，當學生提出問題“為什么估3厘米？而不是1厘米、2厘米……”時，他們的思維是模糊的，筆者通過“你認為3厘米怎樣？”助力學生語言表達的突破，直至引導學生提出“怎么估才準？”。同樣，在教學片段2中，教師通過“以問引問”使得學生能更清晰地表述問題“沒有1厘米了怎么估？”。

學生表達問題的過程就是一個“試誤”階段，教師通過點撥使學生的問題語言由不精準向精準轉變。這里要注意的是點撥需適量、及時，點到為止。

2.問語模糊時，引導生生共振

學生思考初期形成的問題是籠統、模糊的。學生發現頭腦里有些想法，想表達自己的問題時，往往講了半天，別人也不知道他想表達什么。此時，可以讓其他學生補充和提示，使得問題逐漸清晰化。在此過程中，提示的學生得到了鍛煉，提問的學生也能獲得能力的提升。

教學片段1呈現了生生思維共振的畫面，當學生提出“1厘米是干什么的？”這樣模糊的問題時，筆者鼓勵其他學生來幫助其完善問題。由于學生的思維基本處于同一個水平，他們更容易有共鳴及互相理解。完善者與分享者這場“思維的乒乓球比賽”，也能促使更多的學生參與到問題中。

3.思維放松時，鼓勵自由提問

低段學生的問題意識需要被呵護，教師不要為了提問而讓學生去提問。這樣會讓學生常常處于緊張狀態，反而不利于學生提問能力的發展。教師要引導學生的提問由不自覺向自覺轉變，提問不是目的，思考才是目的。

教學片段1中，有學生質疑“1厘米”的作用時，由于大家感覺自己是在幫助同學完善問題，因此心態較輕松，便開啟了自由狀態式提問：“為什么標1厘米，而不是標其他的長度？”“1厘米是不是能幫助我們估計？”“1厘米在這里到底有什么用？”。教學片段2中，在解決完怎么估的問題后，學生處于輕松狀態，在筆者的引導下學生也開始“暢談困惑”。思考問題就是一種思維的活動，教師不要貿然打斷學生的自由提問，而是使學生能更久地處于思考的氛圍中。

總之，學習是一個循序漸進的過程，“發現和提出問題”能力的培養亦是如此。無論新課教學還是習題課教學，教師均應耐心引導學生思問、現問、述問，從而提升學生的數學思維能力和語言表達能力。

【本文系海鹽縣2019年度教育科學規劃微型課題《小學低段數學學生提問的“思·現·煉”策略研究》研究成果。】

（責編 童 夏）