一元線性回歸問題的可視化教學(xué)案例研究

張弛

[摘? ? ? ? ? ?要]? 研究一元線性回歸問題的可視化教學(xué)案例。基于GeoGebra平臺，通過一個具體的實際教學(xué)案例研究不同函數(shù)模型擬合效果、函數(shù)擬合的殘差比較等，實現(xiàn)一元線性回歸問題的教學(xué)可視化，并在與傳統(tǒng)教學(xué)設(shè)計對比后得出可視化教學(xué)具有有效增強教學(xué)效果、提高學(xué)生學(xué)習積極性的結(jié)論。

[關(guān)? ? 鍵? ?詞]? 教學(xué)設(shè)計;GeoGebra;可視化

[中圖分類號]? G712? ? ? ? ? ? ? ? ? ?[文獻標志碼]? A? ? ? ? ? ? ? ? ? ?[文章編號]? 2096-0603（2021）45-0158-02

對于初識統(tǒng)計學(xué)問題的職業(yè)學(xué)校學(xué)生來說，回歸分析問題的學(xué)習對初等函數(shù)知識要求較高，且具有計算量較大、思維抽象的特點。GeoGebra是一款動態(tài)數(shù)學(xué)軟件，同時具備代數(shù)變量運算、統(tǒng)計概率以及3D繪圖等實用功能。GeoGebra軟件通過便捷計算代數(shù)系統(tǒng)和智能指令輸入系統(tǒng)，真正實現(xiàn)了數(shù)與形的融合，將抽象的數(shù)據(jù)關(guān)系可視化為可具體感知的圖像信息，激發(fā)中職生數(shù)學(xué)的學(xué)習興趣，提升學(xué)生的數(shù)學(xué)核心素養(yǎng)。

一、教材解讀

（一）教學(xué)目標與教學(xué)重難點

“一元線性回歸”是江蘇職業(yè)學(xué)校文化基礎(chǔ)課數(shù)學(xué)第十章第八節(jié)的內(nèi)容。其教學(xué)重點是了解一元線性回歸的基本思想與方法，難點是理解回歸模型建立的基本步驟。

（二）傳統(tǒng)教學(xué)設(shè)計流程

茶水銷售問題：商店為了解茶水銷售量與最低氣溫之間的關(guān)系，隨機統(tǒng)計并制作了某六天的銷售量（單位：杯）與當天最低氣溫（單位：℃）的對照表（見表1）。

若某一天最低氣溫為-5℃，能否估計這天商店賣出茶水的杯數(shù)？

在教材中，以此題作為引入問題，要求建立茶水銷售量y關(guān)于氣溫x的一元線性回歸方程。從傳統(tǒng)教學(xué)設(shè)計的角度，此題包括以下三個問題的討論與解決：（1）作出熱茶銷售量與氣溫的散點圖，根據(jù)散點圖建立它們間的函數(shù)關(guān)系;（2）建立以溫度為自變量、茶水銷售杯數(shù)為因變量的一元線性回歸模型，計算殘差并利用殘差進行數(shù)據(jù)分析;（3）計算W（a，b），并利用最小二乘法對建立的模型進行分析，判斷能否較好地刻畫溫度和茶水銷售量間的數(shù)量關(guān)系，最終生成一元線性回歸方程。

二、基于GeoGebra平臺的教學(xué)過程

GeoGebra軟件具有數(shù)據(jù)統(tǒng)計與分析、函數(shù)繪圖和強大的代數(shù)運算功能，故我們利用GeoGebra軟件，針對該課題實施教學(xué)活動。

（一）建立一元線性回歸模型環(huán)節(jié)

1.繪制散點圖

啟動GeoGebra軟件后，在主菜單欄中的“視圖”選項里單擊“表格區(qū)”，則在界面右側(cè)彈出表格區(qū)。然后，在表格區(qū)輸入表1中的“最低氣溫”“茶水銷售量”及對應(yīng)數(shù)量。接著，框選數(shù)據(jù)，通過右鍵彈出對話框，選擇對話框中的“創(chuàng)建”—“點列”欄目。此時，繪圖區(qū)內(nèi)生成數(shù)據(jù)散點圖，即生成點列為l1。

教師在生成散點圖后，再呈現(xiàn)教材中的散點圖，由學(xué)生對兩張圖片進行對比，分析兩張圖片的區(qū)別，再總結(jié)匯報，教師進行點評。學(xué)生會發(fā)現(xiàn)教材中的坐標系的縱軸已經(jīng)進行了縮放，散點分布失真。那么，散點分布的規(guī)律到底滿足什么樣的特征？僅僅依靠直觀印象是不能做出正確的判斷的，由此學(xué)生探究的愿望漸濃，期待進行下一步的探究。

2.建立一次函數(shù)模型環(huán)節(jié)

散點圖生成后教師指導(dǎo)學(xué)生觀察其特征，回顧已掌握的函數(shù)圖像，由學(xué)生猜想并嘗試建立回歸模型。在小組討論后匯報的過程中，大部分學(xué)生都能得出“散點圖分布在一條直線附近”的結(jié)論，也會有一部分學(xué)生猜想二次函數(shù)、冪函數(shù)的情況。針對這一情況，教師要及時給予表揚，引導(dǎo)學(xué)生先嘗試建立一次函數(shù)回歸模型，并將其他情況作為拓展任務(wù)暫不展開。

首先，教師指導(dǎo)學(xué)生在指令欄里輸入“多項式擬合”，彈出“多項式擬合（<點列1>，<多項式次數(shù)>）”指令提示。

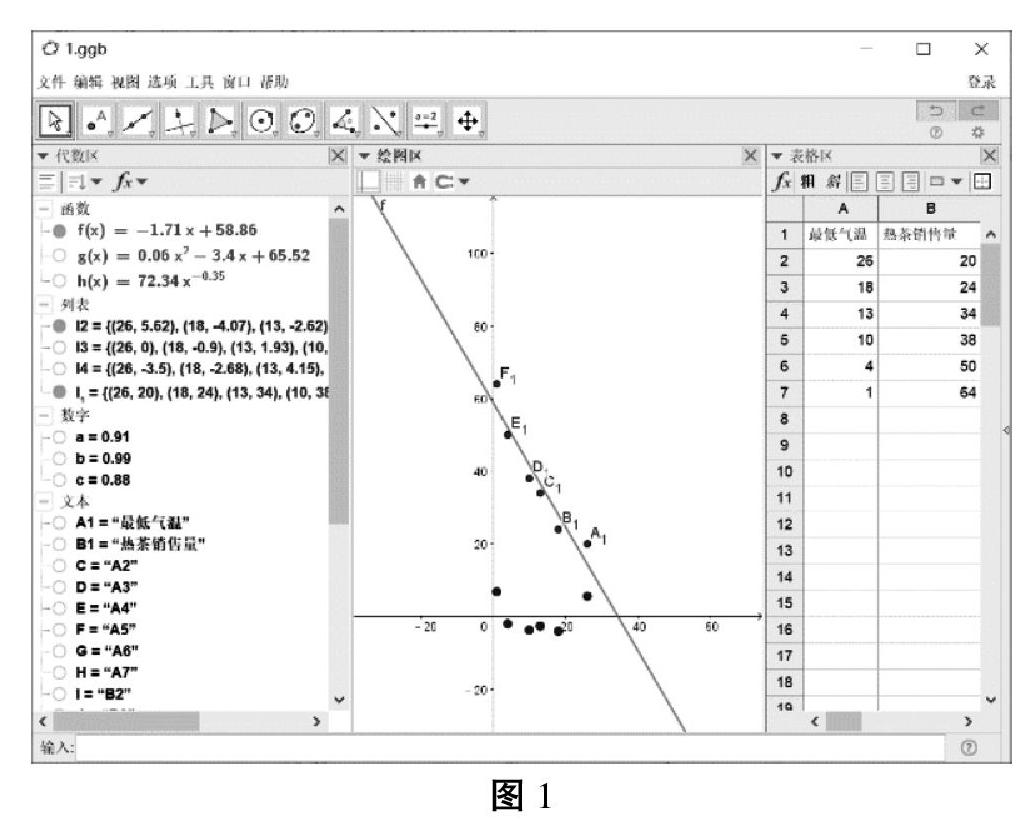
接著，將其中“<點列1>，<多項式次數(shù)>”改為“l(fā)1，1”，并點擊回車后，此時在繪圖區(qū)中生成一次函數(shù)圖像f（x），同時在代數(shù)區(qū)內(nèi)顯示函數(shù)f（x）=-1.71x+58.86，在計算機生成一次回歸函數(shù)后，教師則呈現(xiàn)回歸直線的數(shù)學(xué)定義：用直線方程近似表示的相關(guān)關(guān)系叫作線性關(guān)系，這條直線成為回歸直線，其中a，b稱為回歸系數(shù)。學(xué)生回答出計算機生成的回歸系數(shù)為“a=1.71，b=58.86”。

3.一次函數(shù)模型殘差分析環(huán)節(jié)

教師指導(dǎo)學(xué)生在指令區(qū)內(nèi)輸入“殘差圖”，彈出“殘差圖（<點列>，<函數(shù)>）”，將其改為“殘差圖（l1，f（x））”，則在繪圖區(qū)內(nèi)呈現(xiàn)出一次函數(shù)模型的殘差圖。（如圖1所示）。

在殘差圖的直觀演示下，教師引導(dǎo)學(xué)生將殘差與方差進行對比，促進學(xué)生對殘差這一概念的理解。然后，教師再借助殘差圖，簡要介紹殘差的平方和表達式以及求解回歸系數(shù)的最小二乘法。最后，給出一元回歸直線的系數(shù)計算公式。

（二）回歸模型拓展環(huán)節(jié)

1.建立二次函數(shù)、冪函數(shù)模型環(huán)節(jié)

教師依據(jù)學(xué)生猜想的另外兩種回歸模型：二次函數(shù)與冪函數(shù)模型，指導(dǎo)學(xué)生自主完成計算機繪圖任務(wù)。首先，教師指導(dǎo)學(xué)生在指令欄里輸入“多項式擬合”，彈出“多項式擬合（<點列1>，<多項式次數(shù)>）”指令提示。接著，將其中“<點列1>，<多項式次數(shù)>”改為“l(fā)1，2”，并點擊回車，此時繪圖區(qū)中生成二次函數(shù)的函數(shù)圖像g（x），并且代數(shù)區(qū)內(nèi)會呈現(xiàn)函數(shù)g（x）=0.06x2-3.4x+65.52。然后，在指令欄里輸入“冪函數(shù)”，彈出“冪函數(shù)擬合（<第一象限點列1>）”指令提示。接著，將其中“<第一象限點列1>”改為“l(fā)1”，并點擊回車，此時在繪圖區(qū)中生成冪函數(shù)圖像h（x），同時在代數(shù)區(qū)內(nèi)顯示函數(shù)h（x）=72.34x-0.35。

2.不同函數(shù)模型擬合效果的比較

教師指導(dǎo)學(xué)生作出二次函數(shù)與冪函數(shù)模型的殘差圖。通過學(xué)生先觀察、討論，再分析比較，發(fā)現(xiàn)二次函數(shù)模型的殘差分布于x軸附近，殘差絕對值也較小;冪函數(shù)模型殘差在x軸附近分布較為分散，即殘差絕對值較大，所以得出結(jié)論：二次函數(shù)模型擬合較冪函數(shù)模型好。但學(xué)生也會提出質(zhì)疑：“僅憑直觀感知，沒有計算”是不能作為充分條件的。

因此，教師順勢指導(dǎo)學(xué)生利用R2值驗證猜測結(jié)論。

首先，在指令欄里輸入關(guān)鍵詞“可決系數(shù)”，提示“可決系數(shù)R方（<點列1>，<函數(shù)>），將其中“<點列1>，<函數(shù)>”改為“l(fā)1，f（x）”，單擊回車鍵后，在代數(shù)區(qū)內(nèi)顯示a=0.91（即R2=0.91）。

然后，在指令欄里輸入關(guān)鍵詞“可決系數(shù)”，提示“可決系數(shù)R方（<點列1>，<函數(shù)>），將其中“<點列1>，

<函數(shù)>”改為“l(fā)1，g（x）”，并單擊回車鍵，在代數(shù)區(qū)內(nèi)顯示b=0.99（即R2=0.99）。

最后，在指令欄里輸入關(guān)鍵詞“可決系數(shù)”，提示“可決系數(shù)R方（<點列1>，<函數(shù)>），將其中“<點列1>，

<函數(shù)>”改為“l(fā)1，h（x）”，再單擊回車鍵，在代數(shù)區(qū)內(nèi)顯示c=0.88（即R2=0.88）。

在對三種函數(shù)擬合情況的“可決系數(shù)”進行比較分析時，教師可以向?qū)W生明確R2越大表示擬合效果越好。

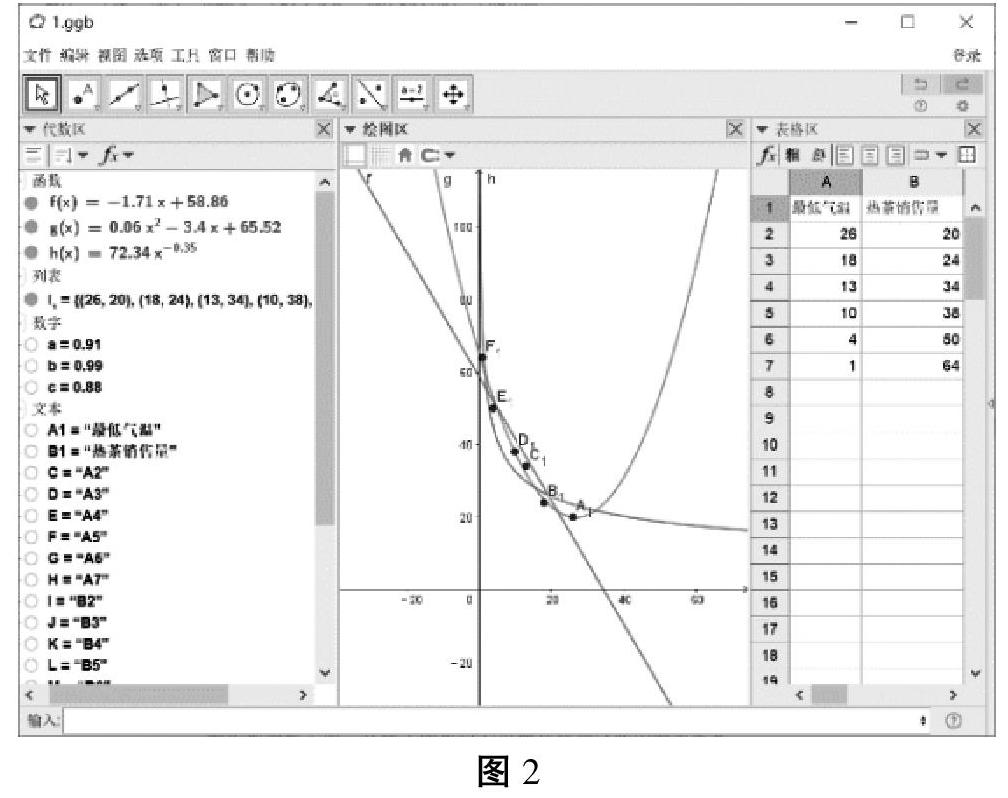
觀察函數(shù)的圖像與相應(yīng)R2值的大小對比，師生可以發(fā)現(xiàn)二次函數(shù)模型擬合的效果最佳，經(jīng)比較甚至比教材中提供的一次函數(shù)模型擬合的效果更為精密，但是冪函數(shù)模型的擬合效果是三者中最差的。再將三種模型刻畫在同一坐標系之中則更具視覺直觀性（如圖2所示）。故而可以借助二次函數(shù)解析式對-5℃的情況預(yù)測小賣部賣出茶水的杯數(shù)。

三、兩種教學(xué)設(shè)計效果分析

基于GeoGebra軟件的教學(xué)設(shè)計，給課堂教學(xué)創(chuàng)設(shè)了一個學(xué)生大膽猜想、自主探索、即時生成的學(xué)習情境。首先，本次課的設(shè)計節(jié)省了學(xué)生手動作圖及計算的時間，學(xué)生參與思考、交流討論的意識得到加強。其次，相比傳統(tǒng)的教學(xué)設(shè)計，本次設(shè)計拓展了二次函數(shù)與冪函數(shù)模型的探究，這產(chǎn)生于GeoGebra軟件可視化效果作用下的課堂即時生成。最后，相比較傳統(tǒng)教學(xué)設(shè)計中直接引入殘差平方值的計算，GeoGebra軟件中殘差圖的運用更具直觀性，有利于學(xué)生從直觀感知過渡到理性認知，進一步進行針對幾種函數(shù)模型進行主動解構(gòu)與對比。所以，本課題的教學(xué)設(shè)計中生成的二次函數(shù)擬合程度較好的結(jié)論，是相對于教材中一次函數(shù)模型更加合理的一種函數(shù)模型的呈現(xiàn)，是一種機智的教學(xué)生成。

參考文獻：

[1]張志勇.高中數(shù)學(xué)可視化教學(xué)：原則、途徑與策略：基于GeoGebra平臺[J].數(shù)學(xué)通報，2018，57（7）：21-24，28.

[2]張維忠，唐慧榮.可視化教學(xué)內(nèi)容設(shè)計的五大原則[J].電化教育研究，2010（10）：99-102.

[3]李紅美，王鎮(zhèn)國，韋俊楠.面向移動終端課堂互動信息的可視化分析：以高中數(shù)學(xué)為例[J].現(xiàn)代教育技術(shù)，2017，27（2）：113-119.

◎編輯 鄭曉燕