淺議微積分學中的“化”

蘇 志 勇張 飛 羽

（1.蘭州大學數學與統計學院，甘肅 蘭州 730000；2.河西學院數學與統計學院，甘肅 張掖 734000）

在微積分學課程的學習中，學生對定理的理解程度，對知識的運用能力，體現在具體的解題過程中.培養學生具有正確得當的解題思路，是教學過程中的重要一環，是對目標教學與結構教學是否有機結合的一種檢驗.這里所要談的“化”，是數學中的一種分析和解決問題的重要方法.在此，如果我們把已知的事實、假設、定理、公式稱之為“標準型”，把待論證或計算的問題稱之為“非標準型”，那么貫穿整個微積分學的思想之一，就是化非標準型為標準型來解決問題（這也是其它數學學科常用的方法）.課程教學中常用的方法有兩類，一是恒等變形，在這里也僅僅是分項組合、加減或乘除同一數（式）；另一個就是變量替換.這里的變量替換手段包括RMI原則，即關系映射反演原則，其含義是：假設我們遇到的問題為原像關系結構R，R中原像目標為Z，并且R在中難以解決，為此我們尋找一種可定映射?，將問題R轉化成R?，R?中映像目標為Z?，并且能夠通過確定的數學方法解出Z?，然后再通過反演?-1，將原像求解出來.基于此，文中精選了較為充分的例題，除了體現函數的分析性質之間轉化具體形式（恒等變形和變量替換）外，還考慮了建構模式轉化問題（譬如：微積分學中理論構造性的證明，數學模型的構建，等等）.同時，所選的典型例題都能體現化歸思想在分析中的應用.

1 極限理論中的化

這方面的問題有兩類，一是直接論證或計算極限A，另一類是給定極限A，求極限B.前者所用依據有：極限的定義、兩個重要極限、等價無窮小、夾擠定理、單調有界原理、柯西收斂準則、洛必達法則等等.當然，微積分幾乎所有的概念和定義都是由極限定義的，它們反過來也可用于極限討論；對后者，一般方法是：將B或B的部分形式化成A（或A的拓展形式）來求解.與此相反的作法就是利用f(x)=A?f(x)=A+α,將其代入極限B中討論.當然，對上述兩類問題，變量替換法也常常或顯或隱地在使用.

1.1 直接論證

提示 通過有理化方法，把其中的極限為零的因子n4+1-n4化去，使之變為常見的形式.

1.2 已知極限A,求極限B

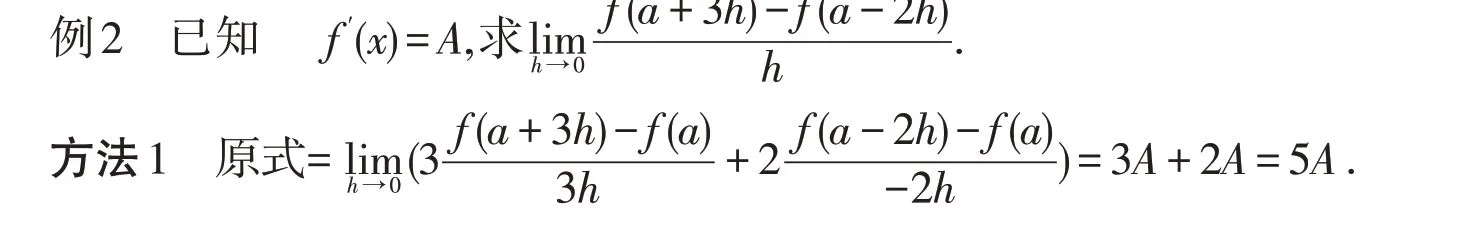
方法2

2 利用函數構造進行轉化

在函數的連續性理論和可微理論中，函數構造法比較普遍.例如，用零點定理證明介值定理，以及用洛爾定理證明拉格朗日中值定理和柯西中值定理等.

例4f(x)∈C[a,b],f(a)b??ξ∈(a,b) ,f(ξ)=ξ.

提示 令g(x)=f(x)-x?g(a)?g(b)<0.

3 利用互逆關系進行轉化

常用的互逆關系有：函數與反函數、微分與不定積分、方程（組）與其決定的隱函數（組）、函數展成冪級數與求冪級數的和函數等.例如，等式兩邊取對數法；利用函數的導數與不定積分計算其反函數的導數與不定積分，如

隱函數存在定理在求曲線的切線方程、曲面的切平面方程、化條件極值為無條件極值等方面扮演著重要角色，如拉格朗日數乘法公式的建立.

例8 求曲面x=x(u,v),y=y(u,v),z=z(u,v)在點M處的法向量.

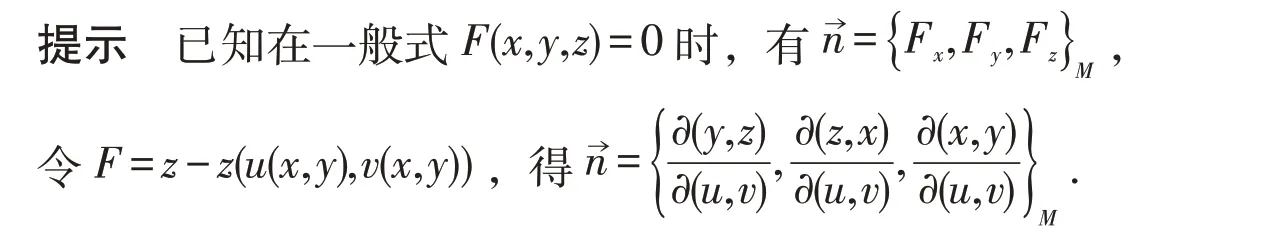
4 利用一些“橋梁”性定理進行轉化

（1）利用海因定理，將數列極限的理論用于一般函數，反之亦然，如洛必達法則用于數列極限的計算；

（2）利用微分中值定理及泰勒公式，將函數的性質及特征轉化成其導數或高階導數的性質，反過來研究函數，如函數的單調性、凸性、極值、切線斜率、曲率、近似計算、零點個數估計等；

（3）利用積分理論中的格林公式、高斯公式、斯托克斯公式，進行不同類型積分之間的轉化；

（4）利用對無窮區間的分化，進行級數與廣義積分之間的轉化，如

5 利用函數的局部屬性與整體屬性進行轉化

有限覆蓋定理和區間套定理就是局部性質與整體性質之間進行轉化的橋梁，如用有限覆蓋定理證明連續函數在閉區間上有界，以及用區間套定理證明零點定理.有時在鄰域內選取小閉區間也可達到此目的，如冪級數分析性質的論證.另外，最值點即有整體屬性又有局部屬性，所以它在一些問題的論述中扮演著重要角色，如洛爾定理的證明，一些不等式的證明等.

6 利用常量與變量的辯證關系進行轉化

將常量關系轉化成變量關系，這一方法在數項級數求和、一些橢圓積分的計算、柯西-施瓦茲不等式的證明等問題中比較常見（如例5）.反之，在局部視變量為常量，以及利用累次法、折線法、固定變量法進行一元函數與多元函數之間的轉換，就是將變量關系轉化成常量關系很好的例子.

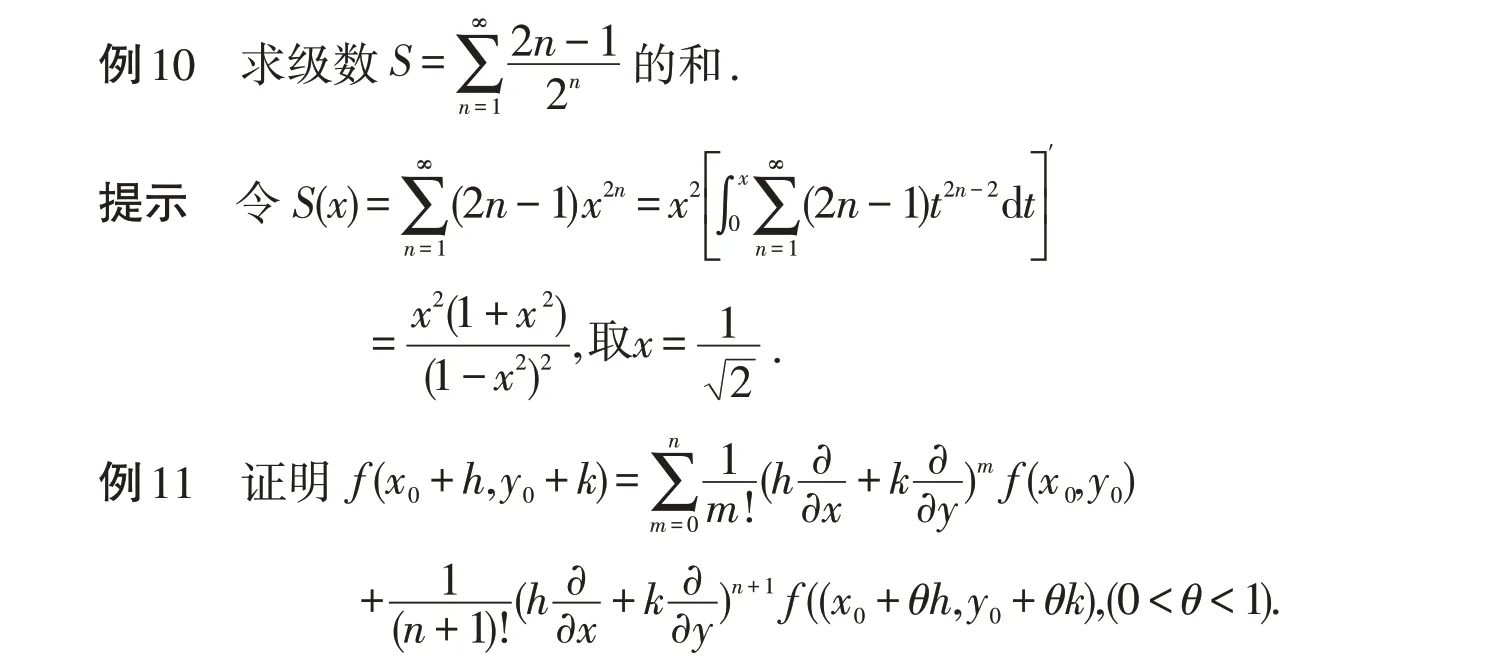
提示 這是關于定點(x0,y0)與其附近點(x0+h,y0+k)的局部問題，在兩點連線上構造一元函數?(t)=f(x0+ht,y0+kt)，給出其馬克勞林展式后代入

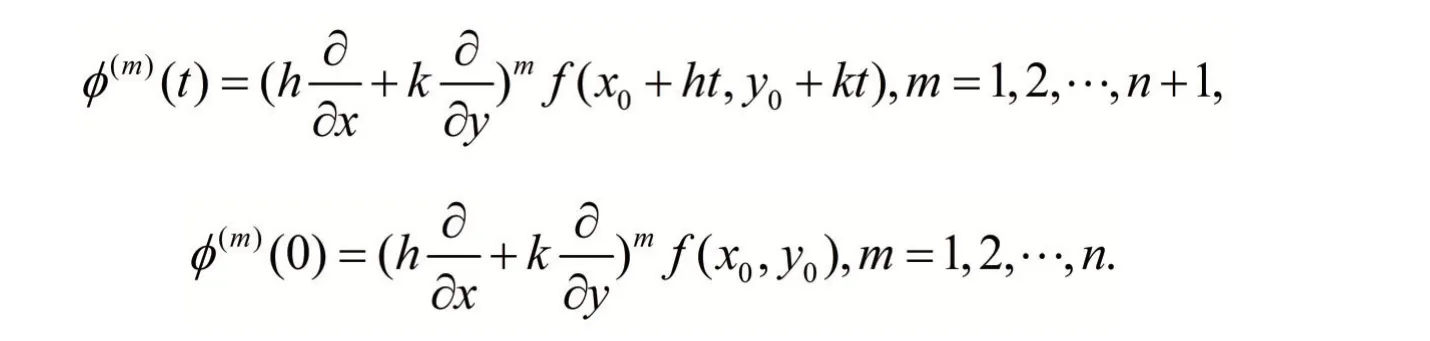
例12 設f(x),g(x)∈R[ ]

a,b，證明施瓦茲不等式

7 利用極限將無限（界）形式轉化成有限（界）形式

一般在“有限”情況下，許多性質、運算都成立，如四則運算、兩種運算次序的交換等.而微積分的主要內容都體現“無限”，為此，我們常常化“無限”為“有限”加極限，如無窮級數與廣義積分分析性質的論證.另外，值得一提的是，有限覆蓋定理的應用，它利用命題中每一點的局部性質構造出開鄰域簇，再將“無限”問題轉化為“有限”問題來處理，如利用有限覆蓋定理證明連續函數在閉區間上有界.

提示 兩種積分次序的交換可在區間有限的情況下進行.?A>a，考慮

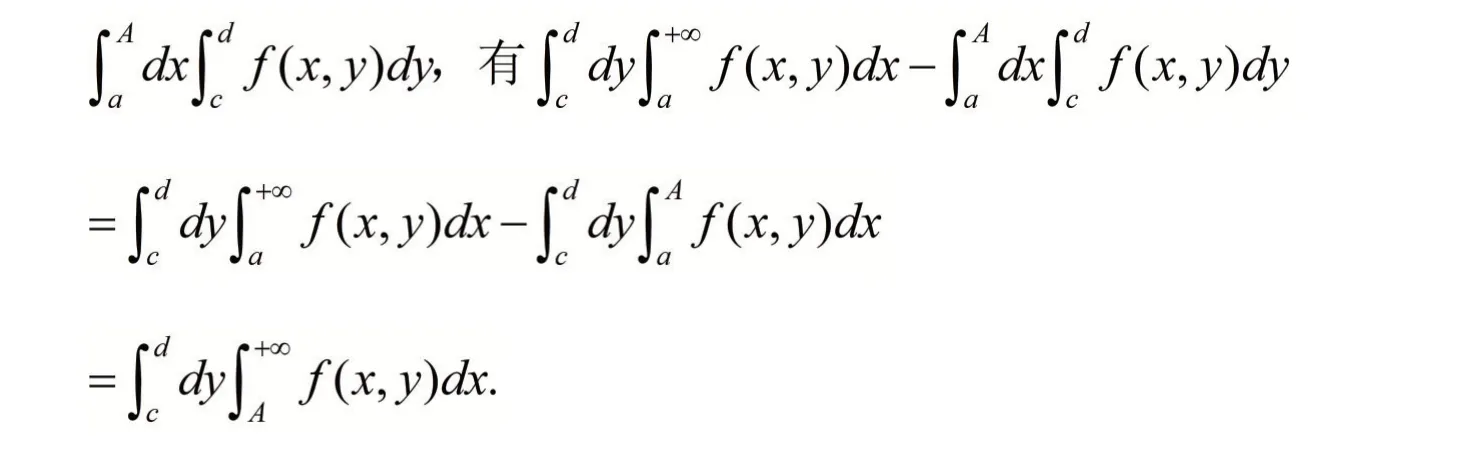
再利用一致收斂性即可.