基于數學核心素養的滲透教學

文|王倩

一、數學核心素養的內涵分析

數學核心素養是指小學生在數學學習過程中應當達成的、有特定意義的綜合性能力，包括“直觀想象、模型思想、空間觀念、數學運算、抽象思維、邏輯推理、數據分析”等數學思想與數學能力。這些數學思想與數學能力具有持久性、整體性、綜合性等特點。

二、數學核心素養的重要性分析

數學核心素養雖然不是具體的教學內容，但卻反映了數學最本質的特點與內在價值，是促進小學生形成數學思維、數學思想和數學知識技能的源動力。數學核心素養不僅是小學生學習數學必備的思維與技能基礎，更是小學生學習其他學科，以及將來必備的思維與技能基礎。

例如，具備邏輯推理能力，能讓學生運用合理假設、科學論證、歸納類比等方法認清事物本質、發現事物規律，促進學生形成嚴謹縝密、條理清晰的思維方式和學習態度，不僅有利于提高學生的數學學習效率，也有利于提高他們學習其他學科的效率，更有利于學生將來養成嚴謹高效的工作態度與有條有理的處事風格，讓學生更能適應將來的工作環境與社會生活。具備數學運算與統計分析能力，不僅能提高學生解決數學問題的效率、提高學生數學學習的自信心，而且能為瞬息萬變的社會培養大批高科技后備人才。因為互聯網技術已經滲透到社會各行各業，云計算、大數據離不開數學算理與算法，而小學階段是培養學生數學運算、數據分析能力的基礎時期，夯實小學生的計算基礎就是為學生的人生打好底色。

可見，培養小學生的數學核心素養，就是從數學的角度幫助學生養成良好的思考習慣，獲得必需的知識與技能，形成良好的思維能力與方法態度。這不僅是小學生學好數學的必要能力，更是學生將來自立于世的必要技能。因此，小學數學教師應高度重視培養學生的數學核心素養，并把培養核心素養滲透到教學的各個方面，讓學生在潛移默化與日積月累中形成屬于自己的獨特數學核心素養。

三、數學課堂滲透核心素養的途徑

（一）在質疑提問中滲透核心素養。

問題意識是引發小學生數學學習與思考的基礎，也是激發小學生探究真相、發現規律的不竭源泉。因此，教師應在教學中借助多種教學手段創設有趣的問題情境，喚醒學生的問題意識，激發學生的質疑能力，誘發學生去主動思考與探究。

例如，教學《比的意義》時，為了激發學生的問題意識與探究興趣，我設置了懸疑問題情境。首先，播放了一段公安人員在犯罪現場偵查、尋找犯罪線索的視頻讓學生觀看：公安人員在現場提取了一枚腳印，測量其長度為25 厘米，并根據腳印長度推算出犯罪嫌疑人的身高為175 厘米左右。接下來，我問學生：你們對視頻中的案件偵查有什么疑問，或者對哪些細節感興趣呢？學生紛紛舉手，他們提出的問題很多，如“為什么公安人員根據腳印長度就能推算出犯罪嫌疑人的身高？公安人員是用什么方法計算犯罪嫌疑人身高的？”等等。看到學生的好奇心被激發起來，我出示了一組數據讓學生自己尋找答案：1.人的身高與雙臂平伸的比約是1∶1；2.成年人腿長與頭長的比約是4∶1；3.體重與血液質量之比約為13∶1；4.一般成年人的身高與腳長的比約是7∶1……學生一看，恍然大悟：原來公安人員是根據身高與腳長的比（7∶1），25×7=175（厘米），所以很快推算出犯罪嫌疑人的身高。我告訴學生，“比”在我們的生產生活中隨處可見，如做米飯時應按怎樣的比例放米和水？建大樓時應按怎樣的比例放沙子、水泥和水？我再讓學生舉出生活中更多的“比”的事例，學生都爭先恐后地舉手回答。接下來，我引導學生從事例中發現，“比”的用處很大，也為我們的生產生活提供了極大便利。那么，究竟什么是“比”？怎樣求“比值”呢？（板書：比的意義）學生露出好奇的表情，他們對學習“比”產生了強烈的愿望，接下來的教學活動就是順勢而為，我引導學生運用觀察、比較、分析、概括等一系列方法，層層推進探究“比”的內涵與比值的求法。由于前面的問題情境鋪墊，學生在整個學習活動中積極踴躍，學習效率也非常高。

其實，上面是運用了生活化的問題情境，把抽象的數學概念變得直觀化、形象化，以誘發學生的問題意識與直觀想象，激發學生思考的興趣與探究的愿望。這正是培養學生抽象思維與分析概括能力必不可少的情感與思維基礎。

（二）在合理猜想中滲透核心素養。

學習數學離不開猜想與假設，因為猜想是培養學生想象與創新的重要途徑。因此，在數學教學中，我們要鼓勵小學生大膽猜想、合理假設，引導學生在猜想引領下，經歷觀察、實驗、推理、論證等探究活動，鍛煉學生的數學思維，提升學生的數學核心素養。

例如，教學《圓的面積》時，我通過引導學生一次次提出猜想，再一步步驗證猜想，最終引導學生推導并提煉出圓的面積計算公式。

教學時，我先以話題導入：學校要建一個新花壇需要知道哪些數據？（應知道花壇面積、再根據花壇面積計算所用的花苗）然后讓學生回顧圓的周長公式，并啟發學生猜測：圓的面積計算可能與哪些因素有關？（周長？直徑？半徑？）從而引出新課內容。

1.把圓轉化為正方形數小方格驗證。

我先用多媒體畫了一個正方形，再以正方形的邊長為半徑畫圓，從而把圓的面積計算轉化為數小方格計算（每個小格為1 平方厘米）。由于“正方形的面積=16 平方厘米”“圓的面積≈13 平方厘米”“圓的面積≈13×4=52 平方厘米”，而“52÷16≈3.1……”，因此可以得出“圓的面積≈正方形的面積×3=邊長×邊長×3”；因為“正方形的邊長=圓的半徑（r）”，所以“圓的面積≈半徑×半徑×3=半徑2×3”。

通過實驗驗證了圓的面積與半徑有直接關系，且是半徑平方的三倍多。那么是不是所有圓的面積都與半徑有關，且都是半徑平方的三倍多呢？

2.學生自主實驗進一步探究驗證猜想。

我讓學生用上面的實驗方法自主操作并完成下面表格。先用透明方格紙分別數出一大一小兩個正方形的面積；再分別以這兩個正方形的邊長為半徑畫圓，用數方格的方法分別數出兩個圓的面積；再讓學生用計算器算出兩個圓的面積，以及圓的面積是正方形面積的幾倍。

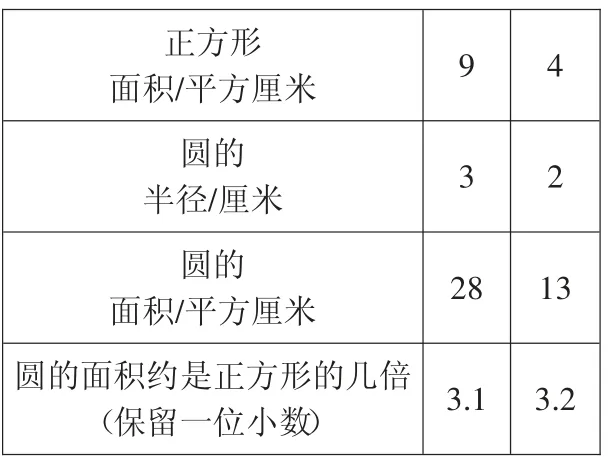
正方形面積/平方厘米94圓的半徑/厘米32圓的面積/平方厘米2813圓的面積約是正方形的幾倍（保留一位小數）3.1 3.2

讓學生觀察上表的數值，發現這兩個圓的面積都是它半徑平方的三倍多。由于圓周率π≈3.14，是不是圓的面積與π 有關系呢，也就是“圓的面積是否是π 乘以半徑的平方”呢？

3.利用動畫輔助驗證并推導面積公式。

為了驗證“圓的面積是否是π 乘以半徑的平方”，我借助多媒體運用了“轉化”的方法進行驗證，也就是利用動畫演示把一個圓形平均分成8 份、16 份、32份、64 份……再把分出的份數拼成一個新的圖形。學生通過觀察動畫演示發現，把圓平均分的份數越多，拼出的圖形就越接近長方形。由于拼出的長方形的長是圓周長的一半（長方形的長=、寬是圓的半徑（寬=r），因此可以得出：圓的面積=長方形的面積=簡化一下就是πr2。從而順利推導出圓的面積計算公式就是“S=πr2”，同時也驗證了圓的面積與圓周率π 有直接關系。

（三）在數學建模中滲透核心素養。

在小學生的思維結構中，數字只代表整數，對應著具體實物（如1 個人，10 個球），要在他們頭腦中建立分數、小數等非整數概念，是一件非常困難的事情。因此，教師可以由數軸等幾何圖形入手，幫助學生建立數形關聯，再引導學生把圖形語言轉化為抽象的非整數概念。

例如，教學《小數的意義》一課時，可以利用數軸的直觀特點引導學生聯系已有知識經驗，通過假設、探究、討論、推理等學習活動，得出“小數的意義”這一概念，讓抽象的概念變得直觀可感。

1.縱向聯系，明確換算關系。

（1）利用數軸引導學生回憶“米、分米、厘米”之間的換算關系。（1 米=10 分米=100 厘米）

（2）引導學生觀察數軸，思考探究。

①把1 米平均分成10 份，每份是（ ）；用分數表示就是（ ）米。

②把1 米平均分成100份，每份是（ ）；用分數表示就是（ ）米。

2.橫向聯系，由舊知向新知遷移。

（1）把1 米平均分成10 份，用小數怎樣表示？

思路引導：把1 米平均分成10 份，每份是“1 分米”，用分數表示就是“米”，用小數表示就是“0.1 米”，因此“1 分米=米=0.1 米”。

（2）如果把1 米平均分成100 份，用小數該怎樣表示？（學生自主推導）

3.探求規律，完成新概念建構。

（1）按照上面的推理方法，讓學生自主探究。

①把1 米平均分成10 份，取其中的一份，用分數表示是（ ）米、用小數表示是（ ）米，如果取其中的2 份和4 份，用分數和小數表示分別是多少？

②把1 米平均分成100 份，取其中的5 份和7 份，用分數和小數該怎樣表示？

……

（2）探究后交流，得出：分數和小數之間有直接聯系，不同的分數可以寫成不同的小數。

（3）引導學生總結、概括小數的意義。

在上面的學習活動中，利用數軸幫助學生進行思考、探究、推理，把“抽象”的小數變得直觀可感，把“深奧”的“小數意義”變得簡單形象，從而幫助學生順利完成關于“小數的意義”的概念建構。