應(yīng)用統(tǒng)計學(xué)專業(yè)實踐教學(xué)案例的量化分析

胡 攀

(四川文理學(xué)院 數(shù)學(xué)學(xué)院, 四川 達(dá)州 635000)

0 引 言

《國家中長期教育改革和發(fā)展規(guī)劃綱要(2010-2020 年)》中提出了在人才培養(yǎng)體系改革中要“注重知行統(tǒng)一”,“堅持教育教學(xué)與生產(chǎn)勞動、社會實踐相結(jié)合”,突出強調(diào)了高校在人才培養(yǎng)工作中加強大學(xué)生實踐教學(xué)培養(yǎng)的重要性.[1]應(yīng)用統(tǒng)計學(xué)專業(yè)具有較強的實踐性、應(yīng)用型和綜合性特點,而實踐教學(xué)是本專業(yè)人才培養(yǎng)方案的重要組成部分.實踐教學(xué)不僅可以培養(yǎng)學(xué)生的創(chuàng)新精神和實踐能力，而且能培養(yǎng)學(xué)生理論聯(lián)系實踐,提高實際動手能力和分析問題、解決問題的能力.

為了全面深入貫徹落實黨的十九大精神和習(xí)近平新時代反腐倡廉建設(shè)的新思想、新部署和新要求.四川文理學(xué)院數(shù)學(xué)學(xué)院受川東A市紀(jì)委委托,對本市轄區(qū)范圍內(nèi)58個申請創(chuàng)建“廉潔細(xì)胞”的單位,按照六大類“廉潔細(xì)胞”的建設(shè)標(biāo)準(zhǔn),通過問卷調(diào)查的方式進行第三方監(jiān)測評估,以鞏固和發(fā)展A市良好的政治生態(tài).數(shù)學(xué)學(xué)院接到任務(wù)后,深知本次監(jiān)測評估工作即是一項艱巨的政治任務(wù),更是應(yīng)用統(tǒng)計學(xué)專業(yè)一次難得的實踐教學(xué)機會.通過本次實踐活動,既可以加強應(yīng)用統(tǒng)計學(xué)專業(yè)實踐教學(xué)內(nèi)容與考核方式的建設(shè),又可以培養(yǎng)學(xué)生的創(chuàng)新精神和實踐能力,還可以檢驗本專業(yè)的教學(xué)質(zhì)量.

傳統(tǒng)的應(yīng)用統(tǒng)計學(xué)專業(yè)的實踐教學(xué)研究,主要是從定性的角度進行分析和總結(jié).[2-5]從定量的角度進行分析和研究的成果少之又少.因此,本文以川東A市六類“廉潔細(xì)胞”工程建設(shè)中“廉潔機關(guān)”的建設(shè)為例,通過問卷調(diào)查的方式，綜合運用數(shù)學(xué)建模和描述性統(tǒng)計的思想和方法,對10個申報建設(shè)“廉潔機關(guān)”單位的調(diào)查問卷進行量化分析,探索應(yīng)用統(tǒng)計學(xué)專業(yè)實踐教學(xué)的過程和內(nèi)容設(shè)置,希望能加快完善本專業(yè)的實踐教學(xué)體系.

1 調(diào)查問卷設(shè)計概述

做好應(yīng)用統(tǒng)計學(xué)專業(yè)的實踐教學(xué),既是提高本專業(yè)人才培養(yǎng)質(zhì)量的重要保證,也是培養(yǎng)學(xué)生理論聯(lián)系實踐的主要途徑.作為應(yīng)用型與實踐性較強的專業(yè)，要搞好實踐教學(xué),關(guān)鍵是做好兩方面的工作:一方面是做好抽樣與調(diào)查；另一方面是運用恰當(dāng)?shù)姆椒▽Τ闃诱{(diào)查的結(jié)果進行整理和分析.抽樣與調(diào)查作為實踐教學(xué)的主要內(nèi)容,既是前期獲取高質(zhì)量調(diào)查數(shù)據(jù)的保證,又是后期對調(diào)查結(jié)果整理和分析的基礎(chǔ).因此,做好抽樣與調(diào)查環(huán)節(jié),能使實踐教學(xué)達(dá)到事半功倍的效果.本節(jié)結(jié)合川東A市“廉潔細(xì)胞”工程建設(shè)中“廉潔機關(guān)”的建設(shè),介紹調(diào)查問卷內(nèi)容的設(shè)置與抽樣方法的選取.

1.1 調(diào)查問卷內(nèi)容的設(shè)定

根據(jù)川東A市紀(jì)委《關(guān)于對“廉潔細(xì)胞”創(chuàng)建示范單位進行考評驗收的通知》要求，本次監(jiān)測評估需對“廉潔細(xì)胞”建設(shè)情況和整治“群眾最不滿意的10件事”活動成效進行監(jiān)測評估.基于此,本次評估將調(diào)查問卷的內(nèi)容設(shè)置為:機關(guān)制度設(shè)定、機關(guān)作風(fēng)、宣傳教育、社會評價和整治活動成效五個方面.

1.2 抽樣方法的確定

為了全面了解川東A市“廉潔機關(guān)”建設(shè)的成效，依據(jù)調(diào)查問卷的內(nèi)容，按照分層抽樣的方法，將各申報點的調(diào)查對象分為中層及以上機關(guān)領(lǐng)導(dǎo)、機關(guān)普通員工和機關(guān)服務(wù)的群眾三個層.考慮到機關(guān)單位中,中層及以上領(lǐng)導(dǎo)人數(shù)較少,采用隨機抽樣可能會造成較大誤差,所以,對機關(guān)領(lǐng)導(dǎo)采用整群抽樣的方式進行問卷調(diào)查.根據(jù)黃金分割比,對機關(guān)普通員工按照62%的比例進行隨機抽樣.由于部分機關(guān)的服務(wù)群眾具有人數(shù)多、分布廣、調(diào)查難度大的特點.因此,監(jiān)測評估小組到各機關(guān)單位的辦事窗口隨機抽取100名群眾進行問卷調(diào)查.[6]各機關(guān)單位的調(diào)查內(nèi)容、題目數(shù)量和抽樣方法見表1.各機關(guān)單位抽樣總體分布及問卷整理結(jié)果見表2.

表1 各機關(guān)單位調(diào)查內(nèi)容分配明細(xì)

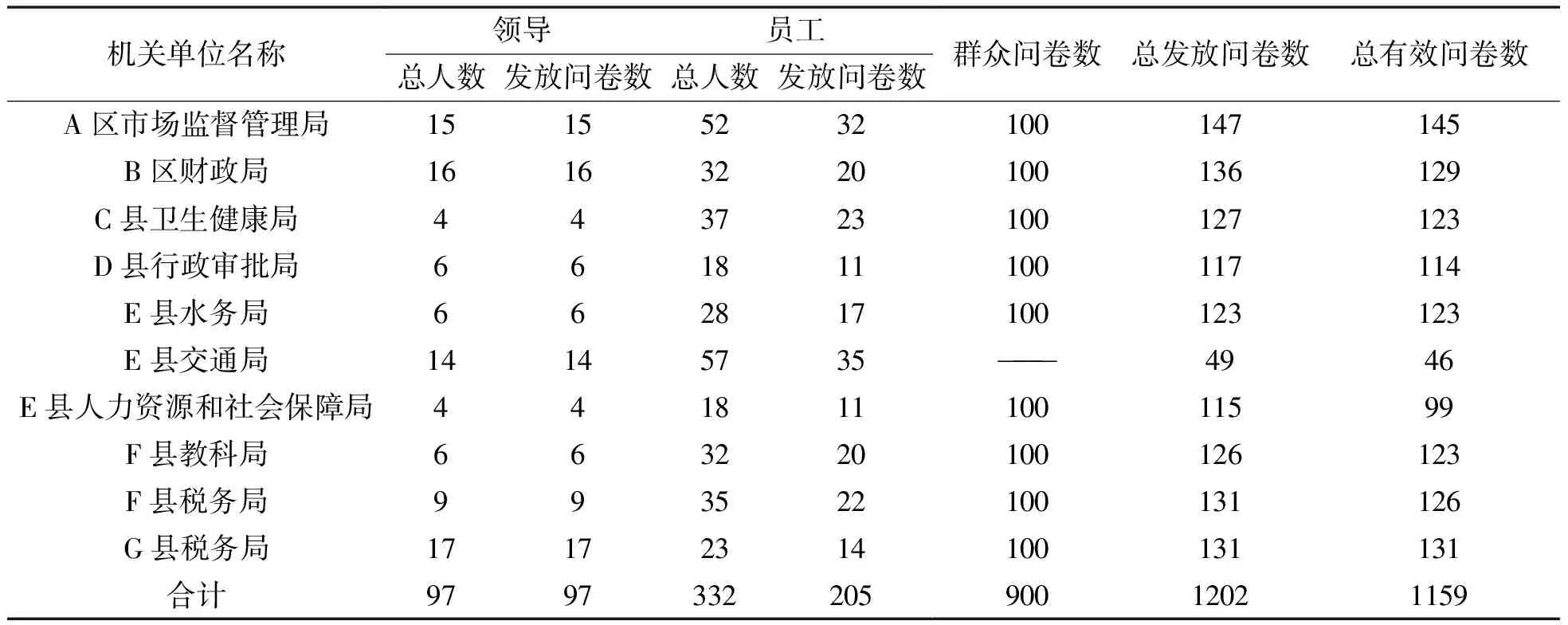
表2 各機關(guān)單位抽樣總體分布及問卷整理結(jié)果

將調(diào)查問卷的結(jié)果錄入excel表格中,將未填寫完整的問卷、填寫過程中存在邏輯錯誤的問卷及部分答案選擇不明確的問卷均視為無效問卷,整理過程中共刪除無效問卷43份.表2中總有效問卷數(shù)=總發(fā)放問卷數(shù)-無效問卷數(shù).

2 監(jiān)測評估成績統(tǒng)計的數(shù)學(xué)模型

問卷調(diào)查結(jié)果的整理和分析是應(yīng)用統(tǒng)計學(xué)專業(yè)實踐教學(xué)的另一項主要內(nèi)容,運用恰當(dāng)?shù)臄?shù)學(xué)統(tǒng)計方法分析調(diào)查結(jié)果,從分析中發(fā)現(xiàn)問題、提出問題進而解決問題,這既可以培養(yǎng)學(xué)生將所學(xué)基本知識和基礎(chǔ)理論用于解決實際問題的能力,又可以進一步探索專業(yè)實踐教學(xué)的內(nèi)容和考核方式.為了對“廉潔機關(guān)”的問卷調(diào)查結(jié)果進行量化分析,并最終以百分制的形式對10個機關(guān)單位的廉政建設(shè)成效進行排名.本節(jié)借助數(shù)學(xué)建模的思想和方法,建立問卷成績計算的數(shù)學(xué)模型.[7]

2.1 權(quán)重系數(shù)的確定

首先將 “廉潔機關(guān)”調(diào)查問卷中的問題分為正向問題和反向問題兩類;其次,依據(jù)每小題的答案選項設(shè)置答案權(quán)重,并將每小題的答案權(quán)重分為普通權(quán)重和特殊權(quán)重兩類.規(guī)定：① 每小題中積極性和正向性強度越強的答案，權(quán)重系數(shù)越高,反之亦然.② 對于問卷中選項后面留有填空的題目,領(lǐng)導(dǎo)和普通員工如果選了對應(yīng)選項，但選項后面填空內(nèi)容留空白,視本小題權(quán)重為0,如果選了對應(yīng)選項,依據(jù)選項后面的填空內(nèi)容設(shè)置特殊權(quán)重(如:領(lǐng)導(dǎo)問卷中的第8小題,員工問卷中的8、9小題);③ 對于題目后面沒有選項只有填空的小題,將根據(jù)問卷答案設(shè)置特殊權(quán)重(如:群眾問卷的第7小題).最后,結(jié)合每小題的答案選項數(shù)量和強度等級(強度等級由強到弱依次定為I級、Ⅱ級、Ⅲ級和Ⅳ級)，制定各答案的權(quán)重系數(shù). 特殊權(quán)重系數(shù)范圍[0,1],普通權(quán)重系數(shù)見表3.

表3 不同答案選項的普通權(quán)重系數(shù)

2.2 監(jiān)測評估成績統(tǒng)計的數(shù)學(xué)模型

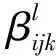
(1)

由于三類調(diào)查問卷的題目數(shù)量各不相同,各小題的賦分結(jié)果也不盡相同,造成三類調(diào)查問卷的總分均不是百分制,不便于后續(xù)統(tǒng)計分析和排序.因此，需要先對三類調(diào)查問卷的實際得分作如下百分制轉(zhuǎn)化:

(2)

記nij表示第i個監(jiān)測點第j類問卷的問卷份數(shù),從而可得第i個監(jiān)測點第j類問卷的平均得分為:

(3)

記α1,α2,α3分別表示領(lǐng)導(dǎo)、員工和群眾問卷得分在總評成績中的比重.綜上可得監(jiān)測評估成績的數(shù)學(xué)模型:

(4)

3 監(jiān)測評估成績統(tǒng)計與分析

3.1 監(jiān)測評估成績統(tǒng)計

結(jié)合上節(jié)的數(shù)學(xué)模型,編程求出川東A市“廉潔機關(guān)”建設(shè)10個監(jiān)測評估點的考評成績及排名如表4.

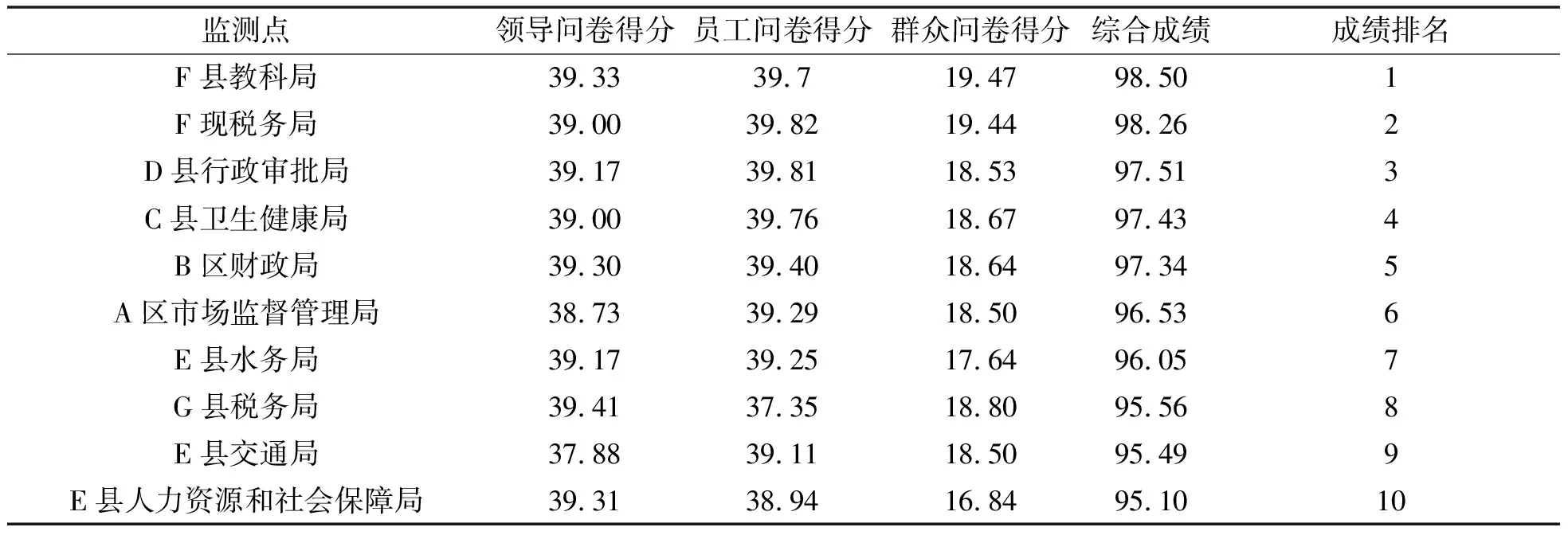
表4 監(jiān)測評估點考評成績及排名

由于E縣交通局的原因,造成本單位的群眾問卷缺失,在成績處理過程中,將其余9個單位群眾問卷的綜合成績?nèi)∑骄笞鳛镋縣交通局的群眾問卷得分.表中的問卷得分是在問卷得分百分制轉(zhuǎn)化基礎(chǔ)上乘以總評得分權(quán)重系數(shù)后的結(jié)果,權(quán)重系數(shù)α1,α2,α3分別取0.4,0.4和0.2.

3.2 考評成績統(tǒng)計分析

(1) 描述性統(tǒng)計分析

從表4的數(shù)據(jù)統(tǒng)計結(jié)果可知,10個監(jiān)測評估點領(lǐng)導(dǎo)問卷平均得分39.03,最高得分39.41,最低得分37.88,極差為1.53;機關(guān)單位員工問卷平均得分39.243,最高得分39.82,最低得分37.35,極差為2.47;群眾問卷平均得分18.503,最高得分19.47,最低得分16.84,極差為2.63.

(2) 綜合成績結(jié)構(gòu)對比分析

10個“廉潔機關(guān)”監(jiān)測評估點的綜合成績差異不大,為了看清各監(jiān)測評估點綜合成績差異的本質(zhì),將10個監(jiān)測評估點領(lǐng)導(dǎo)問卷成績、員工問卷成績和群眾問卷成績繪制成如下蜘蛛圖.[8]

圖1 各監(jiān)測評估點問卷成績結(jié)構(gòu)對比圖

從圖1可知,E縣人力資源和社會保障局和E縣水務(wù)局群眾得分偏低,是導(dǎo)致兩單位綜合成績排名靠后的直接原因;G縣稅務(wù)局員工得分略低于其它區(qū)縣,也是導(dǎo)致該縣綜合成績偏低的主要原因;E縣交通局機關(guān)領(lǐng)導(dǎo)得分略低,導(dǎo)致其成績排名靠后.

(3)相關(guān)性檢驗

下面討論10個“廉潔機關(guān)”監(jiān)測評估點領(lǐng)導(dǎo)問卷、員工問卷和群眾問卷得分之間的相關(guān)關(guān)系.由于只有10個評估點,數(shù)據(jù)不具有正態(tài)性,不宜使用Pearson相關(guān)性檢驗,此處考慮Spearman秩相關(guān)系數(shù)檢驗和Kendallτ相關(guān)系數(shù)檢驗.[9]

Spearman秩相關(guān)系數(shù)檢驗的假設(shè)為:

H0:ρ=0?H1:ρ≠0

(5)

Spearman秩相關(guān)系數(shù):

(6)

其中,Ri表示Xi在(X1,X2,…,Xn)中的秩,Qi表示Yi在(Y1,Y2,…,Yn)中的秩.其對應(yīng)的檢驗統(tǒng)計量:

(7)

當(dāng)T>tα(n-2)或P(T>tα(n-2))<α?xí)r,拒絕原假設(shè),表明兩變量有相關(guān)關(guān)系,反之則不能表明有相關(guān)關(guān)系.

Kendall于1938年提出另一種與Spearman秩相關(guān)系數(shù)檢驗相似的檢驗方法.設(shè)有n對觀察值(X1,Y1),…,(Xn,Yn),若乘積(Xj-Xi)(Yj-Yi)>0,?j>i,稱數(shù)對(Xi,Yi)與(Xj,Yj)滿足協(xié)同性;若乘積(Xj-Xi)(Yj-Yi)<0,?j>i,則稱該數(shù)對不滿足協(xié)同. Kendallτ相關(guān)系數(shù)統(tǒng)計量:

(8)

在95%的置信水平下,用上述兩種非參數(shù)相關(guān)性檢驗方法進行檢驗,結(jié)果見表5.

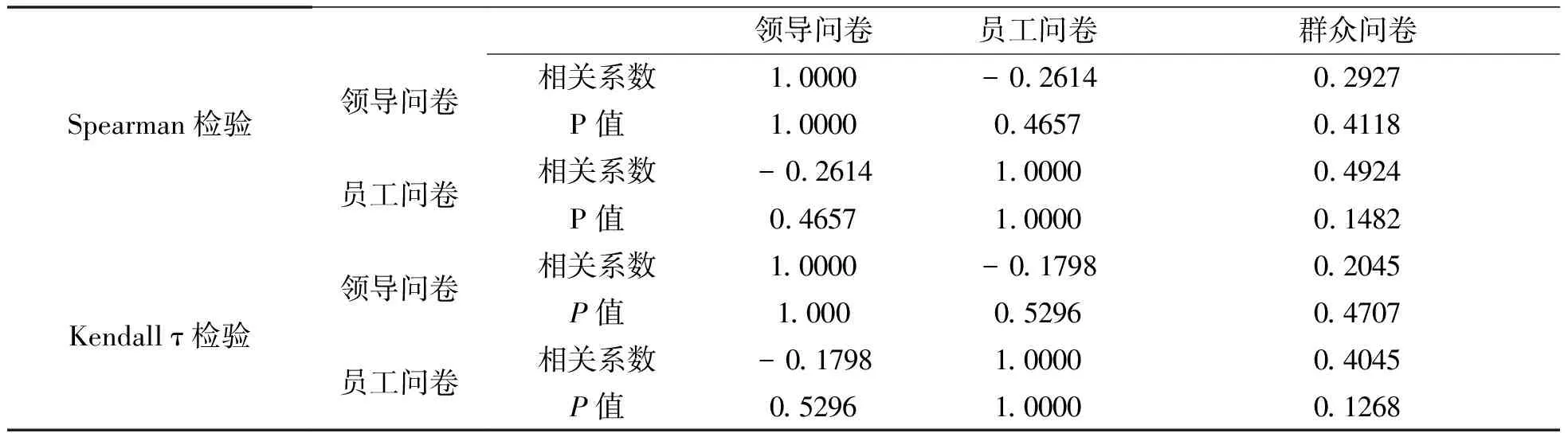
表5 兩種非參數(shù)相關(guān)性檢驗結(jié)果

表5中的數(shù)據(jù)結(jié)果表明,盡管領(lǐng)導(dǎo)問卷、員工問卷和普通群眾問卷的相關(guān)系數(shù)均不為0,但在95%的置信水平下,所有的概率值均大于0.05,故接受原假設(shè),即認(rèn)為三類調(diào)查問卷成績兩兩間不存在相關(guān)性.用上述兩種非參數(shù)相關(guān)性檢驗方法進行檢驗的數(shù)值結(jié)果有一定差別,主要是由兩種檢驗方法的統(tǒng)計量不同造成的,并不影響最終的結(jié)果判定.

結(jié) 論

針對現(xiàn)實生活中的具體實例,將數(shù)學(xué)建模和描述性統(tǒng)計的思想和方法有機結(jié)合起來,從定量的角度,介紹應(yīng)用統(tǒng)計學(xué)專業(yè)實踐教學(xué)的內(nèi)容和方法,具有一定的理論研究意義和實際應(yīng)用價值.用自然科學(xué)的方法解決社會科學(xué)類問題,從方法論的角度看,是一次大膽的嘗試,它將定性的問題轉(zhuǎn)化為定量研究,且數(shù)值研究的結(jié)果表明,此方法具有一定的可行性.前期問卷問題設(shè)置的不足,使得后期在選用統(tǒng)計方法對調(diào)查結(jié)果的分析上顯得過于單一,很難進行深層次的數(shù)據(jù)挖掘與分析,但這并不影響本次監(jiān)測評估結(jié)果的可信度.