二次函數最值題型的歸類及突破
◎王軍南
(甘肅省慶陽市鎮原縣城關初級中學,甘肅 慶陽 744500)
結合自身教學實踐,對二次函數最值問題進行匯總與分析認為二次函數最值題型包括:定軸定區間最值問題、定區間動軸最值問題、定軸動區間最值問題、模型類最值問題、幾何圖形類最值問題、實際問題類最值問題.但無論哪種題型,都需要應用到二次函數的性質,必要情況下需要根據習題創設的情境進行分類討論,因此,在學習的過程中應注重切實打牢基礎,熟練掌握不同題型的解題思路,把握相關的解題細節,尤其保證考慮問題的全面性.
一、定軸定區間類最值問題
相對來說定軸定區間類的習題難度不大.解題時根據題目中給出的二次函數解析式,結合二次函數圖像,確定對稱軸與給定區間之間的關系,結合二次函數圖像性質不難求解出對應的最值.當然部分習題可能不會直接給出二次函數的解析式,解題時需要根據題干中的已知條件先確定其解析式,而后結合二次函數的對稱軸以及給出的自變量范圍求出對應的最值.如下題:
例已知二次函數y=x2+bx+c的圖像經過坐標原點O和A(7,0),直線AB交y軸于點(0,-7),動點C(x,y)在直線AB上,且-1 A.有最小值9 B.有最大值9 C.有最小值8 D.有最大值8 解題思路該習題沒有直接給出二次函數的解析式,但是給出其經過的兩個點,此時可采用待定系數法求出其具體的解析式,而后畫出相關的輔助圖形,找出CD的長與自變量的函數關系.確定函數與對稱軸的大小關系,便可求出對應的最值. ∵二次函數y=x2+bx+c的圖像經過坐標原點O和A(7,0). ∴c=0,49+7b=0,解得b=-7 ∴二次函數為y=x2-7x 又∵直線AB交y軸于點(0,-7),設過AB的直線方程為y=kx+b,將AB兩點坐標代入得到y=x-7,則C(x,x-7),D(x,x2-7x) ∴CD=x-7-(x2-7x)=-(x-4)2+9.可知其表達式為二次函數,其二次函數的對稱軸為直線x=4,又∵-1 解題點評二次函數的定軸定區間最值問題是學生學習二次函數時最先接觸的問題.解題時既需要確定二次函數的對稱軸與區間之間的關系,又需要明確拋物線的開口方向,在此基礎上找到取得最大值的點,將其代入到二次函數中進行計算即可. 解答定區間動軸問題,需要根據題目創設的情景進行分類討論.討論的思路為:對稱軸在區間的左側、對稱軸在區間內部、對稱軸在區間的右側.當然要求解其最值還需要根據二次函數圖像的開口方向,確定其最大值還是最小值.需要注意的是,當對稱軸處在區間內部時,在其頂點處取得最大值和最小值.另外,在確定最后的結果時,需要整合各種滿足題意的結果.如下題: 例當-2≤x≤1,二次函數y=-(x-m)2+m2+1有最大值4,則m的值為( ). 解題思路習題中的自變量范圍為-2≤x≤1,二次函數圖像的開口方向向下.明確這一點后便可按照對稱軸從左到右的順序進行分類討論. ∵二次函數y=-(x-m)2+m2+1,則其對稱軸為直線x=m,頂點為(m,m2+1). (3)當m>1時,二次函數圖像對稱軸在給定區間的右側,則當x=1時取得最大值.代入可得4=-(1-m)2+m2+1,解得m=2. 解題點評定區間動軸類最值問題在初中數學中較為常見.該類問題主要考查學生對二次函數性質的認識與靈活應用程度.因為二次函數的對稱軸是不確定的,所以可將對稱軸按照從左到右的順序,考慮每一種可能的情況.需要注意的是在計算的過程中應注重對相關參數進行合理的取舍. 定軸動區間最值問題和定區間動軸問題類似,均需要進行分類討論.一般情況下分類討論需要分三種情況.當然也有部分習題較為特殊,需要根據已知條件先確定自變量范圍,找到其中的規律,便可減少分類討論的情況.授課中為使學生具體問題具體分析,避免思維定式的干擾,應注重為學生多講解相關的習題,使其掌握不同習題的特點以及對應的解題思路,避免在解題中走彎路,如下題: 例二次函數y=-(x-1)2+5,當m≤x≤n,且mn<0時,y的最小值為2m,最大值為2n,則m+n的值為( ). 解題思路解答該習題不要輕易動筆,應充分挖掘隱含條件,以降低解題的復雜度.由題目中m≤x≤n,且mn<0,便可判斷出m、n和的大小關系,即,m<0,n>0.解題時只需要判斷n和1的大小關系即可. (1)當m≤x≤n<1,由二次函數性質可知,x=m時取最小值,即,2m=-(m-1)2+5,整理解得m=2(舍去)或m=-2.當x=n時取得最大值,2n=-(n-1)2+5,整理解得n=2(舍去)或n=-2(舍去). 解題點評定軸動區間類最值問題區間是確定的,因此在討論其最值時要認真審題,確定是求解最大值還是最小值,而后將區間按照一定的順序移動,結合對稱軸和區間的關系,拋物線的開口方向進行解答. 二次函數最值問題情境復雜多變,解題思路不盡相同.針對以二次函數為背景,求解兩個線段之和最小值的習題,常采用模型法,例如將軍飲馬模型,通過點的對稱,找到點的具體位置,運用幾何知識能很快地求解出最值,因此在解題過程中為少走彎路,提高解題效率,應提高學生的模型應用意識,通過聯系所學的模型,迅速地找到解題的切入點.如下題: 例如圖1所示,已知直線y=kx+b(k,b為常數)分別和x軸,y軸交于點A(-4,0),B(0,3),拋物線y=-x2+4x+1與y軸交于點C,點E在拋物線的對稱軸上移動,點F在直線AB上移動,則CE+EF的最小值為( ). 圖1 A.2 B.4 C.2.5 D.3 解題思路習題要求解兩個線段之和的最小值,先考慮到運用“將軍飲馬”模型,找到C點的對稱點,因C點在拋物線的圖像上,其對稱點也在拋物線的圖像上,且兩點關于拋物線的對稱軸對稱.意識到這一點后,習題也就不難解答. 如圖2,設點C關于拋物線對稱軸的對稱點為C′,由對稱性可知CE=C′E.則CE+EF=C′E+EF,要想其值最小,則只需C′、E、F三點在一條直線上且其所在直線和直線AB垂直. 圖2 解題點評解答二次函數模型類最值問題時應通過審題確定習題考查的是哪一種模型,模型中涉及哪些參數,題干中給出了哪些參數,還需要求解哪些參數等,而后運用所學求解出相關線段的長以及坐標,確定最值對應的參數. 解答幾何圖形內最值問題時常根據已知條件設置相關參數,構建對應的函數,借助函數的性質進行解答.其中構建二次函數求解圖形類最值類問題時既需要靈活運用所學的幾何知識,包括三角形全等、三角形相似、等腰三角形、圓的相關性質等,找到相關參數之間的內在聯系.構建二次函數時為保證求解最值問題的正確性,應注重找到正確的自定義范圍,結合二次函數性質計算出最終結果. 例如圖3,已知圓O的半徑為3,弦CD=4,A為圓O上不與點C、點D重合的一動點,連接AO并延長交CD于點E,交圓O于點B,P為CD上一點,當∠APB=120°時,AP·BP的最大值為( ). 圖3 A.4 B.6 C.8 D.12 解題思路習題要求兩個線段乘積的最大值,結合所學不難聯想到三角形相似的性質總“兩三角形相似,對應邊成比例”,可將其轉化為兩條線段的乘積形式.同時考慮到求最值,需要構建對應的函數.認識到這些內容,便不難找到解題的思路. 如圖4,延長BP交圓O于點F,連接AF、CF、BD,∵∠APB=120°,∴∠APF=60°,又∵AB為圓O的直徑,∴∠AFB=90°,∴∠FAP=30°,∴AP=2PF,∴AP·BP=2PF·BP;由圓周 角定理可得∠FCP=∠PBD,又∵∠CPF=∠BPD,∴△CFP∽△BDP,∴CP/BP=FP/DP,PF·BP=CP·DP,設CP=x,∴DP=4-x(0 圖4 解題點評求解幾何圖形類最值問題不僅需要靈活運用所學的幾何知識求解出相關參數包括線段、角度、點的坐標等,而且需要結合已知條件合理設出相關參數,尤其當將問題轉化為二次函數問題時應注重通過配方法確定其對稱軸,結合自變量范圍進行解答. 二次函數與人們的生產生活有著密切的聯系,在解決實際問題中有著廣泛的應用,尤其在求解實際問題中的最值問題時,使用二次函數可獲得事半功倍的效果.運用二次函數實際問題的最值問題,常出現在初中數學各類測試中.解題中,應結合自身經驗把握相關參數之間的內在邏輯關系,明確自變量與因變量,構建對應的二次函數,運用二次函數性質進行探討. 解題思路該題以人們生活中的產品銷售為背景進行設問.通過審題可知其涉及較多的參數,準確找到參數之間的關系是解題的關鍵,因此既需要認真審題,又需要應結合自身的生活以及解題經驗,理清解題的思路. 解題點評運用二次函數求解的實際問題類的最值問題,關鍵如何構建正確的二次函數模型.解題時應把握以下兩點:其一,認真審題,提煉出有用信息.其二,根據題干描述以及自身生活經驗,通過合理的抽象確定參數間的函數關系,尤其針對不同自變量范圍下對應不同的函數關系時應注重分類討論. 二次函數最值問題情境靈活多變,是各類測試以及中考的熱門考點.部分學生因分類討論的意識不強或者未掌握分類討論的技巧,在解題的過程中非常容易出錯.教師在授課中需幫助學生掌握該類題型,在對二次函數基礎知識深入講解的基礎上對最值問題分門別類,并講解相關的解題思路,尤其在課堂上講解經典例題時,要與學生一起剖析解題過程,使學生留下深刻的印象,布置專題訓練習題,要求其在課下解答,從而達到及時鞏固所學,積累豐富的經驗,掌握相關的技巧的目的.二、定區間動軸類最值問題


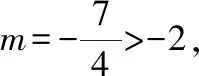

三、定軸動區間類最值問題



四、模型類最值問題


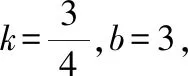

五、幾何圖形類最值問題


六、實際問題類最值問題
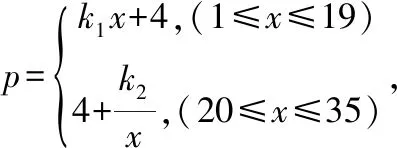

七、總 結

