情境問題解決中的學生認知發展

夏小剛 鄧清

夏小剛

貴州師范大學數學科學學院教授、博士生導師、副院長，教育部高等學校數學類專業教學指導委員會委員;已在《比較教育研究》《數學教育學報》《人民教育》《民族教育研究》《課程·教材·教法》《數學通報》《Journal of Mathematics Education》等期刊發表“數學情境的創設與數學問題提出”等論文，出版《基于提出問題的數學教學研究》等著作;曾獲國家級教學成果一等獎等獎勵，以及貴州省高等學校教學名師、貴州省優秀教師等榮譽稱號。

隨著新課程改革的不斷深化，我國數學教育已逐漸從注重知識的掌握發展到注重基于情境問題解決的數學素養培養。為此，我們需要對情境問題解決中的學生認知發展情況做必要的分析和反思，以探尋面向核心素養培養的數學教學的切入點，為教師有效實施問題解決教學提供參考。

一、調查設計

20世紀90年代末，蔡金法教授以貴陽市小學五年級學生為研究對象，對中美學生在數學情境問題中的認知表現做了一系列的實證研究。為了研究近20年來我國五年級學生在情境問題解決中的認知發展情況，筆者選用了與蔡金法教授所選的同樣的6所公辦學校的五年級學生為研究對象。其中3所學校教育質量高于貴陽市平均水平，另外3所處于貴陽市平均水平。筆者從每所學校選取中等水平的一個班的學生進行測試，得到有效問卷276份。

測試采用了蔡金法教授編制的3份問卷。卷一涉及18個較為簡單的情境問題，卷二和卷三分別涉及6個較為復雜的情境問題，其中卷二的問題屬于過程受限問題，卷三的問題屬于過程開放問題。這3份測試卷的信度系數分別為0.78、0.66和0.72。

二、調查結果與分析

1.問題解決結果差異性與均衡性并存

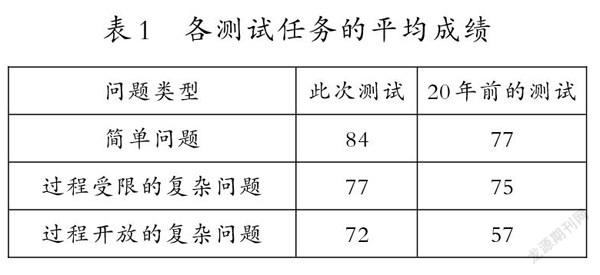
表1顯示了學生在較為簡單的情境問題（簡稱“簡單問題”）、過程受限的復雜的情境問題（簡稱“過程受限的復雜問題”）和過程開放的復雜的情境問題（簡稱“過程開放的復雜問題”）上的數學表現。

由表1可見，學生在簡單問題（t=6.60，p<0.001）、過程受限的復雜問題（t=2.12，p<0.05）和過程開放的復雜問題（t=14.22，p<0.001）的解決上，得分均高于20年前，且差異顯著。學生在3個測試任務上的數學表現各有不同，但與20年前相比，這種差異已明顯減小，且呈現相對均衡的發展狀態。

2.問題解決策略體現多樣性和創造性

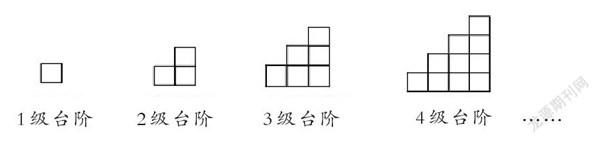
學生在解題策略上幾乎與20年前的情況一致，即大部分學生都采用了常規策略。此外，有不少學生采用了非常規性解題策略，有的解題策略是在20年前的測試中沒有出現的。如“臺階問題”，學生被要求根據下圖求20級臺階的方塊數。

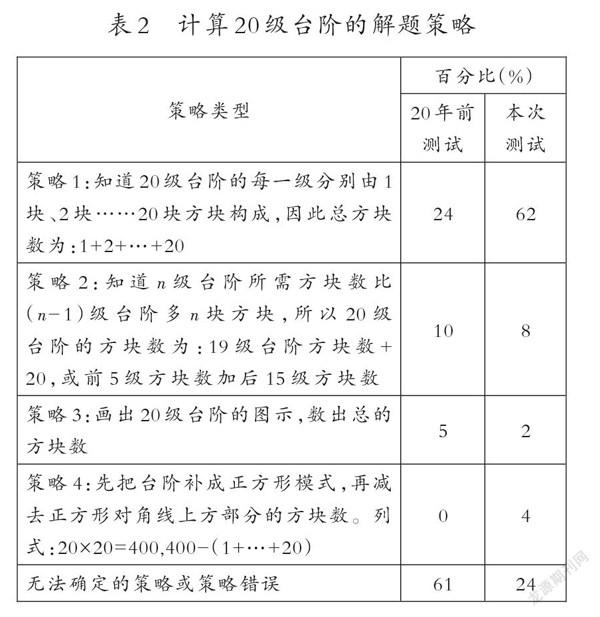
筆者用表2呈現了兩次測試中學生計算20級臺階所使用的解題策略。

可以發現，本次測試中有76%的學生采用了恰當的解題策略，這一比例明顯高于20年前（39%）。采用恰當解題策略的學生中，能正確求出方塊數的占比為78%（20年前為38%）。在正確求解的學生中，62%的學生使用了“高斯方法”，這一比例也明顯高于20年前（30%）;還有少數學生采用了“畫圖計數”策略（如表2中策略3）以及“添補”策略（如表2中策略4）。由于“添補”策略是先把階梯形添補為正方形，再從所得到的方塊總數中減去后添加的方塊數，所以這種解題策略抽象度更高。

3.符號表征是主要表征模式

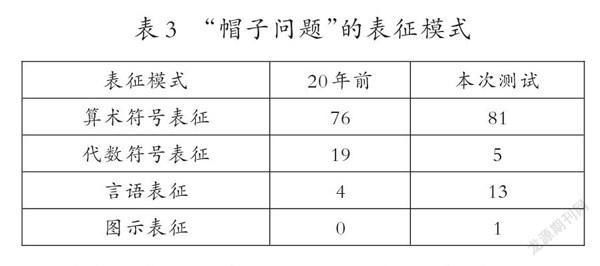
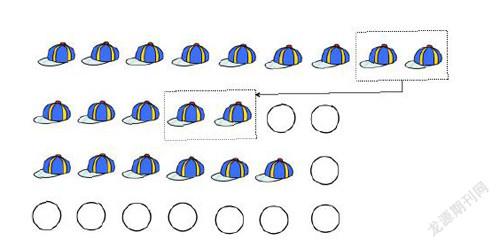
統計結果表明，近20年來采用符號表征的學生占比最多。這在一定程度上反映出學生已經從“直觀思維”過渡到了算術思維，甚至是代數思維。以“帽子問題”為例，該問題以圖示方式呈現了某商店在第一個星期、第二個星期和第三個星期所售出的9頂、3頂和6頂帽子，問這家商店在第四個星期應該賣多少頂帽子，才能使售出的帽子平均數為7。筆者統計了學生表征“帽子問題”的模式（見表3）。

從表3中可以發現，學生兩次解決“帽子問題”時，都主要采用算術符號表征（如9+3+6=18，4×7=28，28-18=10）或代數符號表征（如設第四個星期賣出x頂，由“（9+3+6+x）÷4=7，可知x=10”）。但值得關注的是采用代數符號表征的學生比例明顯減少，采用算術表征的學生比例明顯增加。這一現象值得我們做進一步研究。

4.缺乏對概念性知識的理解

測試中有兩個關于平均數的情境問題。一是“春游問題”（T1）：某小學師生共296人，準備乘車去春游，如果每輛車能坐24人，共需要多少輛車。二是前面提到的“帽子問題”（T2）。前者涉及平均數算法知識的運用，后者體現了對平均數概念的理解。

表4數據顯示：兩次測試中，能正確解答“春游問題”的學生占比均在85%以上，而能正確解答“帽子問題”的學生占比為61%，后者占比明顯低于20年前（71%）。筆者對學生解決“帽子問題”的3種典型錯誤進行統計，發現近70%的解題錯誤涉及平均數概念的理解，如有的學生用前三周所賣的帽子數18除以3，得到6，但是題目中所指的平均數是7，便在前三周的和的基礎上加3，然后除以3，得7，于是錯誤地給出答案“3”。這表明近20年來，學生雖然較好地掌握了平均數的算法，但對平均數的概念性理解水平相對較低，甚至有所下降。

三、調查結論與建議

總體來看，近20年來情境問題解決中的學生認知發展情況呈現以下特點：一是學生解決過程開放的情境問題的能力進步明顯;二是學生解決情境問題的策略更具多樣性和創造性;三是在多種表征共同發展的基礎上，符號表征仍然是學生運用的主要表征模式;四是學生缺乏對概念性知識的深度理解。據此，筆者提出以下建議。

第一，注重情境問題的創設。經過20年的發展，學生解決簡單問題和復雜問題的能力均得到提高，特別是在解決過程開放的復雜問題方面的進步更為明顯。無疑，在基礎教育課程改革背景下，基于情境問題的教學對學生問題解決能力的提升產生了積極作用。但是我們也看到，學生在非常規問題解決上的數學表現不如常規問題，在復雜情境問題解決上的數學表現不如簡單問題。這說明復雜的、非常規的情境問題依然影響和制約著學生對數學問題的分析和解決。為此，教師要注重情境問題的創設。具體來說，在新知引入階段，情境問題的創設應采用學生熟悉的、有利于知識生長和發展的數學情境;在知識應用教學中，情境問題的創設應具有現實性、層次性和開放性，問題的現實性有利于學生從數學的角度觀察和思考問題，問題的層次性有利于不同水平的學生發展數學思維，問題的開放性有利于學生數學綜合能力和創新意識的發展。

第二，鼓勵學生用多種策略解決問題。本次測試，無論是結果還是過程，學生在過程開放的情境問題解決上的數學表現明顯好于20年前。然而，我們也發現仍有較大比例的學生未能根據自己的理解建構恰當的解題策略，甚至放棄問題的解決。在一定層面上，這與下列原因有關：實踐中，教師對學生的自我建構特別是偏離教學目標的數學理解，存在明顯的認識偏差，比如在“列方程解決問題”中，教師對學生采用的算術策略或試誤策略大多不給予積極評價，盡管學生采用這樣的策略也能做出正確的解答。無疑，教師需要關注和鼓勵學生采用多樣化的解題策略，注重學生數學自我認識的建構，激發學生的探究意識，使他們在面對復雜問題時勇于探索，進而發展創新精神，提升實踐能力。

第三，注重學生數學直觀與數學抽象思維的平衡發展。研究表明，學生在解決情境問題時，大多采用較為抽象的解題策略和符號表征，較少使用言語推理策略或視覺表征方式。這符合對小學五年級學生數學認知發展的基本要求，也體現了學生數學思維能力的發展。然而，也有不少采用抽象表征的學生并未正確解決問題，且不少基礎較差的學生不會采用較為簡單、直觀的表征方式。為此，教師要把握學生數學直觀與數學抽象思維的平衡。以“帽子問題”為例，學生的解題錯誤主要在于對符號表征的盲目使用。事實上，換用圖示表征（如下圖），通過“割補”方式解決問題更簡便。

直觀與抽象是數學發展的兩翼。波利亞說：“抽象的道理是重要的，但要用一切辦法使它們看得見，摸得著。”因此，教師應鼓勵學生通過圖示表征等較為直觀的方式，將復雜和抽象的數學對象簡明化、具體化，促進學生數學素養的發展。

第四，注重學生對數學知識的概念性理解。有研究指出，數學概念是從具體情境或數學情境中舍去事物的非本質屬性，保留本質屬性而抽象出來的。調查結果反映出學生對平均數本質理解的缺失，因此，教師不僅要引導學生體會“是什么”，而且要注重概念的多元表征，如實物表征、圖像表征、言語表征、符號表征等，訓練學生轉換不同的表征方式，促進學生對概念本質的認識和對知識的有效運用。

（鄧清，貴陽市烏當中學）

[本文系全國教育科學“十三五”規劃課題“面向核心素養的數學問題情境教學測評模型研究”的研究成果。課題編號：XHA180286]

責任編輯? 劉佳