圓錐曲線上一類定值問題的再推廣

重慶市銅梁二中 (402560) 李 波

1 問題提出

文[1]中給出了圓錐曲線焦點弦引起的所分線段比值之和為定值的若干結論.比如以下兩個結論：

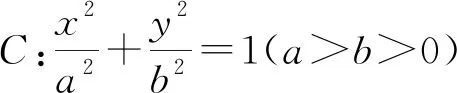
事實上，文[2]也給出了上面的兩個命題，并提供了四種證明思路.在以上兩個結論中，焦點F1,F2其實是x軸上一對關于原點對稱的點.那么，對于x軸上其他的關于原點對稱的點P1,P2，是否有類似的結論？進一步，P1,P2是y軸上的一對關于原點對稱的，甚至是坐標軸之外的一對關于原點對稱的點，λ1+λ2還會是定值嗎？本文對這幾個問題展開討論，并對雙曲線和橢圓上的類似問題給出解答.

2 問題解決

證法同性質1，此略.

圖1

若λ1=-1，則x0=x1,y0=y1，即A,B重合，這不可能.故λ1≠-1.同理可得

遺憾的是,在拋物線上，沒有發現一套與上面的結論完全類似的完整的結論.但是，我們仍然發現一個與性質1相仿的結論.

3 性質1的一個別證

通性通法證明性質1，好處在于容易理解，不足之處是計算實在繁瑣.受文[2]給出的一種方法的啟發，下面將利用圓錐曲線極點與極線的性質給出性質1的另一證明.首先，我們給出一些預備知識.

圖2

引理1 如圖2，D是圓錐曲線Γ外一點，l是Γ關于D的極線，過D的任意直線交于A,B，交l于C，則A,C,B,D是調和點列.

引理2 若點F關于圓錐曲線Γ的極線為l，則l上任意的點關于Γ的極線必過F.

任取l上一點K(x1,y1)，則x1,y1滿足(1)式.從而，x0,y0滿足點K關于Γ的極線的方程，即F在K關于Γ的極線上.

圖3

同理可得，λ2x2=λ2t+t-x0.(4)

定值、定點問題在圓錐曲線的考察中出現頻率較高的一類問題.在平時的教學中，我們應該踐行“為核心素養而教”的教育理念，引導學生積極探究，挖掘問題背后的一般規律，激發學生的學習興趣.