一道2021年上海數學競賽試題的解法探究

山西省太原市第三實驗中學校 (030031) 董立偉

圖1

圖2

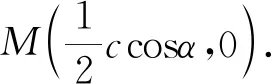
評注：解法中利用“坐標法”的思想，將求CD的長度轉化為求點D的坐標，從而只需想法求出AB、CP、BM三條直線的方程即可.當然，解法是以“點P在線段AB上”和“點D為直線CP與BM的交點”兩個事實為基礎.其本質是“三點共線”.

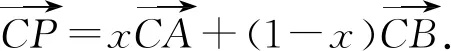
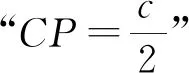
評注：向量法有效地將問題中的長度、角度等幾何關系進行轉化，從而使得問題的解答變得簡單.當然，求解中也可以換一個視角來理解“CP是△CAB的一個頂點C與對邊AB上一點P的連線”這一幾何結構：線段PA和PB是具有一個公共端點的兩條線段，且∠ACP和∠BCP分別是這兩條線段對同一視點C的張角.

解法4：(張角定理1)在△CAB和△CMB中分別使用張角定理，可得

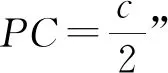
圖3

評注：借助輔助線CO，使得圖形中隱藏的邊角關系變得明朗.事實上，我們確定了含有邊CD的一個三角形△BCD中的一邊BC的長度，并可以確定CD與BC各自的對角.因此，還可以利用正弦定理得到解法6.

評注：本解法充分利用了圖形中的角之間的關系.當然，在△CDM中使用正弦定理也可以給出一個類似的解答.事實上，利用圖中的角與長度，還可以進一步確定一些邊長，比如AP和BP，且不難發現BDM是△ACP的一條截線.

圖4