針對要點防空模型的作戰兵力優化研究
藺向陽, 邢清華, 劉付顯
(空軍工程大學防空反導學院, 陜西 西安 710051)
0 引 言
在現代化聯合作戰行動中,軍隊的防空作戰能力對整體作戰行動有著重要的意義。紅方強大的防空作戰能力不僅能通過遠程威懾和近程輔助航空兵的方式實現對藍方的綜合打擊,削弱藍方空中作戰力量,奪取制空權;更重要是能夠對紅方指揮所、軍械庫、后勤庫等軍事戰略要點進行有效保衛,使其免受打擊,延長在戰爭中生存時間,最大程度發揮其作戰價值,引導戰場平衡向有利于紅方勝利的方向推動。
如何根據藍方的火力配置合理分配紅方兵力,使防空能力達到最強,并對其效能準確評估,是至關重要的。近幾年,在兵力分配的研究中,趙鵬蛟等人分別使用了排隊論、決策論、蟻群算法和模糊決策、Memetic等算法[1-5]。在具體防空作戰兵力分配方面,李菱歌等使用了遺傳算法[6-8],劉寧使用了動態規劃[9],劉立佳等人使用了多目標優化方法[10-11],劉志成和孔祥宇則分別運用了博弈論和圖論[12-13]。邢清華等人則運用建模仿真方法進行了研究[14-18]。同時,在作戰效能的評估方面,羅宇等人采用改進對數法等多種方法對武器效能進行了評估研究[19-23],周立堯等人對不同軍兵種的作戰效能進行了評估[24-26]。外軍方面,Fauske對軍事行動任務規劃進行優化[27]。Mika和Womer使用禁忌搜索等算法對人力和資源調度優化問題進行了研究[28, 29]。Erlandsson使用“生存模型”對軍隊作戰能力進行了評估研究[30]。
國內外專家采用不同的方法研究了兵力優化問題與作戰效能評估問題,但是絕大多數研究的作戰過程都較為單一,難以適用于現階段實際作戰通常具有全領域、多過程作戰的特點。本文立足于當前我國周邊軍事形勢,對某近海區域為作戰背景進行抽象,建立數學模型。基于要點總毀傷期望最低的作戰目標;采用多步建模,層層優化的方法,對近海小規模局部戰爭中聯合防空作戰的兵力配置進行研究;提出一種新的對類二項分布的期望求解方法,實現了對不同層級之間剩余作戰力量的數量期望的準確求解;最終給出與其相適應的評估方法和指標用以對優化效果定量評估,實現優化與評估相統一,使整個模型更加完備。
1 問題描述
取近海區域小規模聯合作戰背景,對實際作戰情況進行抽象,得到作戰示意圖如圖1所示,紅色代表紅方作戰力量,藍色代表藍方作戰力量,靶心代表藍方欲攻擊的紅方要點目標。
紅藍雙方作戰目標與作戰原則可簡化如下。
藍方:通過導彈遠程打擊紅方要點目標,或通過航空兵突進紅方要點上空后投擲彈藥進行轟炸。
紅方:根據情報所得紅藍雙方裝備參數,以及藍方兵力分配,優化紅方兵力分配,攔截藍方攻擊,將要點損失降到最小。
紅方作戰原則:為避免藍方深入,應使用航空兵與艦船將藍方航空兵盡可能攔截在海上。對成功突防的藍方航空兵使用地面防空二次攔截。同時紅方地面防空還承擔對藍方遠程導彈的反導攔截任務。
根據上述任務,對模型作出合理假設如下。
假設 1假設藍方航空兵力量以戰機編隊形式呈現。每組編隊成功突防后具備一次轟炸能力。
假設 2假設紅方航空兵力量和艦船力量都以編隊形式呈現,在海上對藍方戰機編隊進行攔截,二者統一定義為海上攔截作戰力量,簡稱海上力量。每組編隊具備一次攔截能力。
假設 3假設紅方地面防空力量特指地空導彈,簡稱地導力量。每枚導彈為一個作戰單元,具備對藍方戰機編隊的一次防空攔截能力,或對藍方導彈的一次反導攔截能力。
假設 4假設雙方作戰規則為,在單位時間內,藍方特定作戰單元主攻一個要點,對同一要點攻擊的藍方多個作戰單元遵循排隊打擊原則,即不存在兩個打擊力量能精確同時到達。紅方特定作戰單元,只能對藍方一個目標單元進行一次排隊攔截。若目標被友軍提前攔截,則更換對同一要點進攻的下一目標進行攔截。
假設 5假設藍方的總進攻單元數量不多于紅方的總攔截單元數量。否則,必然存在藍方作戰單元不受攔截地對紅方要點進行直接打擊,致使紅方防空任務失敗。
2 模型建立
2.1 模型分析與基礎參數設定
設紅方待保護要點數量為NY,對第k個要點,定義其在受到打擊后,剩余作戰價值與要點完好時總作戰價值的比率為耐久價值Vk,要點完好時Vk0=1。定義要點耐久價值為保衛系數Ek對耐久度Dk的加權。其中耐久度為要點未被摧毀部分所占比率,是承受藍方多次打擊造成的毀傷率的總乘積,要點完好時Dk0=1。保衛系數為相對保衛重NHi要度系數E1k、相對保衛難度系數E2k、相對抗毀傷影響系數E3k的總乘積。其中,相對保衛重要度系數與要點戰略地位呈正相關;相對保衛難度系數與要點位置縱深、隱蔽性和機動性呈正相關;對抗毀傷影響系數與要點對損傷敏感程度呈負相關。
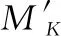
由上可得紅方第k個要點經受藍方第jK種戰機編隊x次轟炸和第jD種導彈y次打擊后,要點耐久度降低為
(1)
要點耐久價值將降低為
Vk=DkEk
(2)
式中:Ek=E1kE2kE3k。則根據作戰目標得待優化目標函數為
(3)
即藍方單位時間的進攻后,紅方總體剩余耐久價值最高。

設已知攔截概率為:第i種海上力量對藍方第j種戰機編隊攔截概率為PHKij(0≤PHKij≤1);第i種地導對藍方第j種戰機編隊攔截概率為PLKij(0≤PLKij≤1);第i種地導對藍方第j種導彈攔截概率為PLDij(0≤PLDij≤1)。而作戰過程中實際攔截概率不僅受制于武器裝備的影響,亦受制于包括雙方的情報能力,指戰員能力,裝備運用程度等主觀能力影響。將其統一設為雙方主觀綜合能力比w(0.1 P=1-(1-P0)w (4) 式中:P為w修正后實際攔截概率;P0為未考慮w的理論攔截成功概率。 由此,即可針對目標函數式(3)對紅方兵力分配進行優化,但由于作戰過程分海上攔截和地導攔截兩個階段,無法直接求解,故使用分布建模,逐級優化的思路,將整個問題分為兩個子過程逐次建模優化。 2.2.1 海上攔截階段兵力分配建模 在此階段,紅方海上力量對藍方戰機編隊攔截。待優化目標函數為 (5) qij=cijPHKij (6) 對式(6)進行w修正: qij=cij(1-(1-PHKij)w) (7) 故目標函數式(5)可等價于: (8) 綜合約束條件,可得完整模型,其中C1,k矩陣為待優化變量。顯然此優化為凸規劃問題,故目標函數的極值點必然是最值點,即C1,k將具有全局最優解。 2.2.2 地導二次攔截階段力量分配建模 由此,可得目標函數: (9) (10) 經w修正為 (11) 同理第2.2.1節,目標函數(9)可轉化為 (12) 式中:C2,k矩陣為待優化變量。 2.2.3 兵力分配效能評估 由上可預測經過本輪作戰結束后,紅方第k個要點剩余耐久度: (13) 剩余耐久價值為 Vk=DkEk (14) 以此可作為本次聯合防空作戰中兵力分配的效能評估指標。 模型建立在對實際作戰中重要參數的抽象提取,確保了模型假設的可靠性。 對于一個復雜的多過程作戰采取分步建模、層層優化的方法。由于每一層優化都是凸規劃,故可以保證各層優化的結果都可取得全局最優解。而結合實際情況與作戰經驗綜合分析確定的紅方作戰原則,即將藍方航空兵盡可能攔截在海上,保證了上層優化所得數據對下層有效,即由上至下到最終優化的結果,一定是在當前排隊打擊的作戰規則前提下,整個作戰過程兵力優化的全局最優解。 效能評估是通過對概率的計算得出的,不僅可得到優化的量化評估值,且此估值具備直觀的現實意義,即紅方要點受損程度的期望值。 根據第2.2.1節中模型,根據式(8)的約束條件,結合相關已知參數與式(7),對式(8)進行優化,可得到最優海上力量分配矩陣C1,k。 3.2.1 問題分析 3.2.2 問題求解 圖2為假設紅方有兩種攔截力量,每種5個編隊,對藍方攔截概率分別為0.8和0.6時,藍方被攔截數量概率分布圖,其中橫軸為攔截藍方數量,縱軸為相應的概率分布。圖2中,綠色是標準正態分布參考線,其中均值為5×0.8+5×0.6=7,方差為5×0.8×0.2+5×0.6×0.4=2。紅色線為藍方數量無限制時,兩個獨立的二項分布構成的攔截藍方數量的概率分布。藍色線和黑色線分別為藍方數量限制在6和8時,兩個類二項分布構成的攔截敵數量的真實概率分布。不難看出,紅線和綠線近似擬合,說明當藍方數量無限制時,其實際概率分布與正態分布近似。而在6之前,藍色點都落于紅色線上,8點之前,黑色點都落于紅色線上,說明在限制之內兩個試驗獨立性不受影響。影響表現在超過上限部分的概率分布,會被統一壓縮在上限點處,如藍色的6和綠色的8處概率激增,之后概率為0。 該期望前項為獨立項期望,后項為非獨立項期望。 (15) 其中,藍方導彈期望為 (16) 藍方戰機編隊期望為 (17) 上文中,通過公式推導與理論敘述說明了算法必然取得全局最優,本節通過一個想定戰例對上述模型及求解算法的可行性與有效性進行驗證。 鑒于保密限制,本文著重研究模型,不涉及相關人員與裝備作戰能力參數的具體信息。 想定作戰背景與參數如下。 (1) 紅方要點信息 數量NY=2。 要點1為某市區指揮所,相對保衛重要度E11=1;固定于市區,相對保衛難度系數E21=0.5;無防御工事,相對抗毀傷影響系數E31=0.2。綜合保衛系數E1=E11E21E31=0.1。 要點2為某機場,相對保衛重要度E12=0.5;位置固定,相對保衛難度系數E22=0.5;機庫具備一定防御工事,相對抗毀傷影響系數E32=0.4。綜合保衛系數E2=E12E22·E32=0.1。 (2) 紅方兵力信息 海上力量種類MH=2,其中戰機編隊H1與艦船編隊H2各有40組,即NH1=NH2=40。 地導種類ML=2,1型地導L1和2型地導L2各20枚,即NL1=NL2=20。 (3) 藍方兵力信息 (4) 藍方兵力對各要點分配情況 (5) 已知紅方對藍方攔截概率P0如表1所示。 表1 紅方對藍方攔截概率表 (6) 藍方毀傷能力 藍方1型戰機編隊一次成功轟炸,對紅方要點造成毀傷比率為1-WK1=0.2,WK1=0.8。 藍方2型戰機編隊一次成功轟炸,對紅方要點造成毀傷比率為1-WK2=0.4,WK2=0.6。 藍方導彈一次成功打擊,對紅方要點造成毀傷比率為1-WD1=0.6,WD1=0.4。 (7) 雙方主觀綜合能力比 紅方與藍方主觀綜合能力相同,即能力比w=1。故w修正后概率:P=1-(1-P0)w=P0 將第4.1節中相關參數代入第2.2.1節模型中,并按第3.1節處理流程,使用Matlab軟件整數規劃,求解得紅方海上力量編隊分配矩陣為 C1,1=C2,2= 0 20 20 0 使用式(15),求得針對各要點藍方在海上攔截階段成功突防的編隊數量期望,對指揮所: 10-9.785 1=0.214 9 對機場: 10-9.785 1=0.214 9 其中,f(x)為滿足期望μ=12,方差σ2=4.8的正態分布函數。 結果表明,紅方海上力量最優兵力分配為:各分配20組戰機編隊攔截藍方2型戰機編隊,分配20組艦船編隊攔截藍方1型戰機編隊。可達到最優效果為:對每個要點,藍方戰機突破紅方海上攔截的1型編隊和2型編隊的數量期望各為0.215組。 將第4.1節中參數和第4.2節中計算所得數據帶入第2.2.2節模型中,按第3.3節處理流程,使用Matlab軟件整數規劃,求解得紅方地導兵力分配矩陣: 按照式(16)和式(17),求得藍方能夠對紅方各要點成功打擊的數量期望。 對指揮所可求得 其中,f(x)為滿足期望μ=9.2,方差σ2=4.32的正態分布函數。 0.214 9-0.205 6=0.009 3 其中,f(x)為滿足期望μ=0.8,方差σ2=0.16的正態分布函數。 0.214 9-0.180 7=0.034 2 其中,f(x)為滿足期望μ=0.6,方差σ2=0.24的正態分布函數。 對機場可求得 結果表明,紅方地導力量最優分配為:對每個要點,各分配10枚1型地導和8枚2型地導用于攔截藍方導彈,分配1枚2型地導攔截藍方戰機1型編隊,分配1枚2型地導攔截藍方2型編隊。整個聯合防空作戰可達到最優作戰效果為:藍方能對紅方每個要點成功實施打擊的數量期望同為1.29枚導彈攻擊,0.009 3次1型編隊轟炸,0.034 2次2型編隊轟炸。 根據第4.3節所得結果,代入式(13)可得到此次聯合防空作戰中,指揮所剩余價值:D1=0.41.29×0.80.009 3×0.60.034 2=0.300 7;機場剩余價值:D2=0.300 7。代入式(14)和式(15)計算得所有要點作戰價值的平均剩余: 以此作為本次聯合防空作戰的兵力分配效能評估值。結果表明,在紅方兵力總數確定時,通過采用最優的分配方案,可以保證在與藍方作戰后,紅方要點仍能發揮的作用價值不低于原有價值的30.07%. 立足于現代化聯合作戰行動,對近海小規模局部戰爭中聯合防空作戰的兵力分配及分配效能的評估進行研究。首先對實際的復雜作戰情況進行抽象得到模型。在已知藍方火力配置的條件下,通過采用分段建模優化,總體概率計算的方法解決了多過程作戰的兵力分配優化問題。提出一種新的方法解決了有限制的類二項分布的期望求解問題。用此方法計算得到藍方各類火力單元成功突防的數量期望,進一步得到紅方要點作戰價值的平均剩余期望,并以此值作為兵力分配防空效能的定量評估值,實現了優化與評估相統一。最后,通過一個想定的戰例,進一步驗證模型與求解理論的可行性與有效性。2.2 模型優化與評估


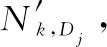
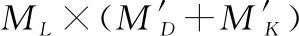
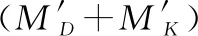
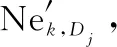
2.3 模型有效性分析
3 模型求解
3.1 海上力量分配求解
3.2 藍方海上突防的真實期望求解
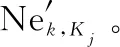
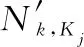
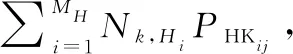
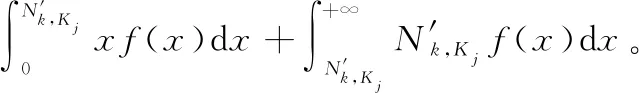
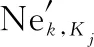
3.3 地導力量分配求解
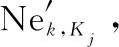
3.4 兵力分配效能估值求解
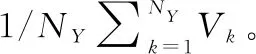
4 實例分析
4.1 背景想定
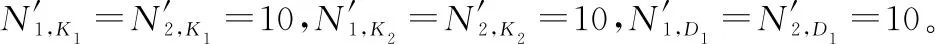
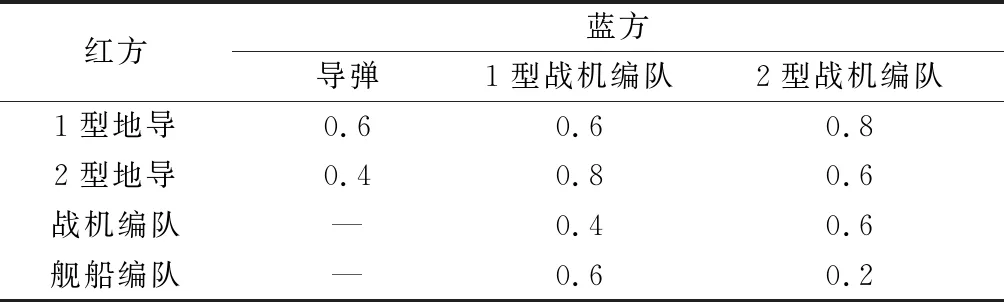
4.2 海上攔截階段求解
4.3 內地反導攔截階段求解
4.4 分配效能估值計算
5 結 論

