高等數學課程中思政教育的融入*

楊瑞龍 梁登星 路云

（1.天津職業技術師范大學理學院；2.北京科技大學天津學院基礎部）

2016年召開的全國高校思想政治工作會議上，習近平總書記指出“要堅持把立德樹人作為中心環節，把思想政治工作貫穿教育教學全過程，實現全程育人、全方位育人，努力開創我國高等教育事業發展新局面”[1]，這一重要指示為當前高校育人工作提供了重要指向。

關于大學數學類課程中融入思政元素有很多的討論。例如，文獻[2-5]給出了一些相關討論。本文討論高等數學課程自身的特點，探討高等數學課程中思政元素的融入。文章首先分析高等數學課堂上開展思政教育的特殊意義，隨后分析了高等數學課堂上開展思政教育的優勢和劣勢。在此基礎上，分析討論高等數學課堂上開展思政教育的可行措施。最后，文章結合高等數學上冊中一節具體的內容“定積分的應用”，具體展示高等數學課程中引入思政元素的實際效果。

一、高等數學課程開展思政教育的特殊意義

（一）高等數學課堂是絕佳的開展思政教育的場所

高等數學是大部分大學學生進入大學后接觸的第一門數學課程，也是涉及專業最多的數學基礎課之一。大一的學生的世界觀和人生觀還在塑造的過程中，在高等數學中，嘗試引入“課程思政”元素，對于培養學生的愛國情操，奠定學生思想教育基礎，有著非凡的意義。作為數學類的課程，高等數學自身也具有優美的邏輯性和客觀性。高等數學的教學中，本身也會貫穿學生邏輯思維和科學素養的塑造。

（二）高等數學課堂自身有開展思政教育的需求

作為一門數學類的基礎課，高等數學的內容較為抽象。具體表現為課時緊、內容多、知識難，學生在學習中多有畏難情緒和排斥情緒，經常抱怨“枯燥”“困難”“不知道有什么用”等，不及格率比其它課程也高。對于高等數學來說，如何“上好課”，是一個尤為重要的課題。高等數學課程中引入思政元素，不僅可以對學生進行思想教育，也可以反哺課程本身，將抽象的數學內容具體化，提升學生的學習興趣，抵消學生對高等數學的抵觸情緒。

二、高等數學課程開展思政教育的優勢及劣勢

相比較其它課程，高等數學課程開展思政教育具有自身的特點。

（一）高等數學課程進行思政教育的劣勢

數學是一門理性的科學，是世界客觀規律的高度抽象。為了內容的嚴謹性，數學往往建立在抽象的符號體系上。這就使得數學類課程理論往往比較抽象，與實際生活缺少直接聯系，開展思政教育有一定難度。另一方面，高等數學內容非常豐富，每節課的知識密度很高，這也導致高等數學課堂的教學時間更加珍貴，需要授課教師加入思政元素的思路更加變通。

（二）高等數學課堂進行思政教育的優勢

高等數學課堂同樣也有一些優勢。1.授課對象是大一的學生，處于知識接收的新鮮期，學生上課投入的熱情和專注度都是很高的；2.大一的學生的價值觀還在成形階段，這個時間思政教育的效果是最好的；3.由于數學是大學考研的必考科目，各專業同學對數學相對重視，高等數學課堂開展思政教育可能有事半功倍的效果；4.大部分的專業高等數學分上下學期，共一學年完成，思政教育比較有連貫性；5.授課對象涉及面積廣，有大量的案例方便教學團隊進行交叉對比，定期總結，反思效果。

三、高等數學中進行課程思政的方法措施分析

高等數學中的課程思政建設，可以沿著如下幾個方面的思路進行：

（一）對接現實，介紹實際應用，讓學生體會知識的有用性

高等數學以微積分為主要內容。微積分的內容起源于牛頓、萊布尼茲等偉大的數學家，并直接催生了第二次工業革命，在實際生活生產領域都有著重要的應用。在課堂中適當地介紹內容相關的應用實例，有助于拉近學生和知識的距離，讓學生意識到數學內容是實實在在有用的，不是空中樓閣，而是各門課程的重要基礎，提高學生的學習興趣。在傳授知識的同時，教育學生重視知識的學習。目前正值中美貿易戰升級之際，國家戰略有產業升級的需求，對高端人才將會有大量缺口。年輕學子要夯實基礎，更好地為祖國建設添磚加瓦。

具體在選擇實例的時候，有以下幾個思路可以參考：

（1）選擇在其它課程或者大學之前數學課上出現過的耳熟能詳的結論。例如：在講解隱函數求導的時候，可以利用它來推導過圓上一點的切線和法線方程，得到“圓上點的法線一定通過圓心”這一在高中數學中熟悉的結論；在講解一元函數的極值的時候，通過費馬最短原理，推導出“光的折射定律”這一物理學中著名的結論；在可降階微分方程一節中，利用可降階微分方程的求解方法，推導高中熟悉的勻變速運動的位移公式。

（2）選擇其它學科中著名的結論。例如：在導數的定義中，介紹經濟學中“邊際”的概念，并解釋經濟學領域經典假設“邊際效應遞減”的實際意義；在方向導數一節中，利用方向導數介紹測繪領域中著名的等高線的含義；在高斯定理一節中，利用高斯定理推導物理學中著名的電通量和磁通量的關系問題。

（二）講述科學發展故事，激勵同學們刻苦奮斗

從最早歐幾里得時代微積分思想的萌芽，到牛頓、萊布尼茲分別獨立提出微積分學基本公式，再到貝克萊主教質疑牛頓的“流數術”進而引起第二次數學危機，最后由阿貝爾、柯西、迪利克雷、黎曼、康托等人完善，形成了目前的微積分體系。高等數學整個課程凝結了幾代數學家的智慧。在授課過程中，可以穿插介紹相關數學家的生平及在微積分完善過程中做的貢獻。進行如下幾個方面的思政教育：

（1）告誡同學們青年時代是最容易迸發創新靈感的，鼓勵同學們在最華彩的年紀要努力學習，努力奮斗，不應該沉溺于娛樂項目中；

（2）整個微積分學科的發展過程可以稱得上是一部波瀾壯闊的史詩，期間充滿了思想的碰撞，更充滿了思想的接力。對于整個過程的把握，也是對同學們一次的精神洗禮，可以培養同學們科學思辨的精神，建立起學生相信科學的信念；

（3）前輩們的成就造福全人類，這種成就不是個人掙錢享受所能比的。引導同學們抵制現在社會上的拜金主義思潮，為了更崇高偉大的理想而奮斗，建立正確的價值取向。

（三）設置特殊數字，挖掘思政元素

在設置例題的時候，可以通過嵌入關鍵數字的方式，使干巴巴的題目或者知識點和重要的歷史巧妙連接起來，數字的選取可以選擇在建黨史上有重要意義的紅色年代。例如：高等數學“定積分的概念”一節中會介紹“奇函數在對稱區間上定積分為0”的結論，這個時候可以引入積分案例，巧妙的把中國共產黨建黨年份或者中華人民共和國成立年份嵌入到學習中。

（四）引入中國古代優秀的數學成就，激發學生的學習興趣

中國古代有非常豐富的數學成就。從遠古時期的商高定理（即勾股定理），到楊輝三角，再到祖沖之計算圓周率，我國數學家很長時間內在數學的一些領域一直處于世界領先地位。直到明末清初，實行閉關鎖國政策，數學才逐漸與西方國家拉開距離。在課程中，通過對這些成果的介紹，一方面可以讓同學們感受古人的智慧。在跟古人神交的過程中，激發同學們的學習興趣；另一方面也激發學生的愛國熱情，弘揚中國文化，增強學生的民族自豪感、培養學生的愛國情懷，強化學生的文化自信；此外，也可以教育學生，落后就要挨打，近代中國的屈辱史，和我國數學及科學的落后是密切相關的。學好科學，才能更好的建設我們的祖國，讓我們的祖國屹立于世界之林，實現中華民族偉大復興。

（五）從授課知識點出發，挖掘辯證唯物主義哲學的內容

從高等數學的知識點出發，也可以挖掘很多思政元素。例如：在“數列的極限”一節，一個很重要的結論是等比數列的極限存在性，即在|q|＜1時收斂，在|q|＞1時發散。這里最重要的是|q|與1的關系，特別地，我們有。

這個公式告訴我們，每天進步一點點，只要持之以恒，我們一定可以達到我們希望達到的高度；而每天退步一點點，最終我們將一事無成。通過這個簡單的公式，可以引導同學們“勿因善小而不為，勿因惡小而為之”的道理，優良品質要從點滴培養，樹立良好的生活習慣和價值觀。

再例如：“方向導數和梯度”一節，一個重要的結論是“當二元函數z=f(x,y)具有連續偏導數fx(x,y)和fy(x,y)，則f(x,y)沿任何一個方向上的方向導數存在，且可以由fx(x,y)和fy(x,y)線性組合得到”[6]。這體現了毛澤東思想之“矛盾論”中的“主要矛盾”理論，“在復雜事物的發展過程中，有許多的矛盾存在，其中必有一種是主要的矛盾，由于它的存在和發展規定或影響著其他矛盾的存在和發展。”在本例中，只要抓住“兩個偏導數”這一主要矛盾，其余的方向導數都可以根據偏導數推出來。

四、具體案例：定積分的應用

本節內容以高等數學上冊“定積分的應用”一節為例，逐一對應上一節中的思政設計思路，結合實例分析思政元素引入的效果。

（一）思政點1：微元法與阿基米德

介紹微元法的時候，穿插講解數學家阿基米德利用“窮竭法”計算拋物線面積的故事，同時介紹阿基米德傳奇的一生。窮竭法最早起源于古希臘數學家安提豐，利用窮竭法安提豐嘗試精確計算圓的面積，并借此推導圓周率的精確值。這幾乎是數學界最早的關于微積分思想的萌芽。利用窮竭法，阿基米德在所著《拋物線求積法》中給出了拋物線弓形面積的定理，即“拋物線弓形的面積，等于對應三角形面積的4/3”。這一結論后來被稱為阿基米德定理[7]。

這個案例中體現了如下思政設計思路：

（1）對接現實，介紹實際應用：拋物線是同學們耳熟能詳的平面圖形，對其弓形面積的計算，能讓同學們感覺到定積分學習的實際應用價值。

（2）講述科學發展故事：通過介紹物理學家阿基米德偉大絢爛的一生，鼓勵同學們積極進取，努力學習。

（3）挖掘辯證唯物主義哲學的內容：同學們一般熟知牛頓與萊布尼茲的故事，會認為微積分是近代數學的成果。通過安提豐、阿基米德的例子，讓學生們了解到，微積分的萌芽古而有之，是無數數學家思想精華的結晶，是無數人知識積累的過程。微積分的建立不是一蹴而就的，整個過程體現了馬克思主義哲學原理中“量變引起質變”的原理。

（二）思政點2：利用微元法推導圓的面積公式

圓的面積公式是同學們耳熟能詳的內容，同學們在小學就已經學習過。但是關于圓的面積公式的詳細推導，大家掌握的并不好。這里通過微元法，給出圓的面積公式的推導。此外，給同學們介紹各個文明分別在不同時間獨立的發現了圓的面積公式的故事。

這個案例中體現了如下的思政元素：

（1）對接現實，介紹實際應用：圓的面積公式是大家在中小學熟知的結論，圓的面積公式的推導體現了微元法的實用價值。

（2）講述科學發展故事：全球各個文明獨立發現圓的面積公式，體現了科學精神的普適性。借此鼓勵同學們投身科研，為人類進步做出貢獻。

（三）思政點3：立體體積與“祖暅原理”

在“平行截面面積已知的立體的體積”部分，引入“祖暅原理”并介紹祖沖之和祖暅父子的成就和崇高地位。祖暅原理是中國古代著名數學家祖暅提出的，在與其父祖沖之合著的著作《綴術》中，祖暅稱“緣冪勢既同，則積不容異”。利用祖暅原理，祖暅計算了牟合方蓋的體積，進而得到了球體體積的計算公式[8]。事實上，祖暅原理是“定積分的應用”中“計算已知截面面積的立體的體積”的一個特殊推論。值得一提的是，祖暅原理在西方被稱為卡瓦列里原理，是17世紀意大利數學家卡瓦列里最先提出來的。而祖暅原理則在公元6世紀就被提出了。

這個案例中用到的思政思路有：

（1）對接現實，介紹實際應用：介紹祖暅原理并推導球體體積公式這一高中時候熟悉的結論，讓學生能更深切的體會到高等數學的實用性。（2）引入中國古代優秀的數學成就：通過對比中外對于祖暅原理提出時間，可以極大地激發同學們的愛國熱情。勉勵同學們要努力奮斗，增強文化自信，為實現中華民族偉大復興奉獻自己的力量。

(四)思政點4：托里拆利喇叭

托里拆利喇叭是數學史上一個很著名的悖論，最早源于數學家、物理學家托里拆利提出的思想實驗。托里拆利是著名物理學家伽利略的學生兼學術助手。托里拆利提出，把定義在[1,+∞)的函數圖像沿x軸進行旋轉，可以得到一個具有無窮長度的立體形狀。由于其形狀類似喇叭，因此被稱為“托里拆利喇叭”。

容易看出，這是一個典型的旋轉體。利用微元法，計算出托里拆利喇叭的體積和表面積，由如下兩個反常積分計算

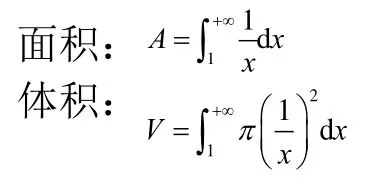
圖1 托里拆利喇叭

可以發現，該立體擁有有限的體積，但是卻擁有無限的面積。這就產生了一個與我們常識不符合的結論：假如一個油漆工要用油漆裝滿整個托里拆利喇叭，只需要有限的油漆即可；但是如果他想將托里拆利喇叭的表面刷滿，則需要無窮的油漆。

這個案例中使用的思政思路是：通過講解數學史上著名的數學悖論，讓學生感受數學發展過程中的思辨精神，培養學生的科學精神，抵制迷信思潮。

五、結語

全面實施課程思政，是目前高等教育界的共識。本文探討了如何有效地在高等數學課堂中進行帶有課程思政元素的課程設計，一方面為了推進高校課程思政建設，另一方面也是為了提升高等數學課程的趣味性、加深學生對于知識的理解，促進學生提升知識并形成自主的思維能力。