拋物線背景下的三角形屬性問題探究

王鳳娥

[摘? 要] 拋物線背景中的三角形屬性問題十分常見，其中三角形的周長和面積問題需要轉(zhuǎn)化為線段長，同時綜合點坐標(biāo)來構(gòu)建思路. 文章將結(jié)合實例探究問題的突破策略，并反思總結(jié)，關(guān)注探究重點.

[關(guān)鍵詞] 拋物線;三角形;屬性;模型;數(shù)形結(jié)合

拋物線背景下的三角形面積和周長問題十分常見，問題突破需要合理處理條件，結(jié)合模型轉(zhuǎn)化問題，下面深入探究.

問題呈現(xiàn)

問題 在圖1所示的平面直角坐標(biāo)系xOy中，已知拋物線的解析式為y=ax2+bx+c，頂點坐標(biāo)M（1，-4），與x軸的交點為A和B，與y軸的交點為C（0，-3），與直線l：y=kx-k-2的交點為D和E，試回答下列問題.

（1）試求拋物線的解析式;

（2）當(dāng)S=5S時，試求k的值;

（3）如圖2所示，過點D作y軸的平行線，與EM的延長線相交于點F，試求當(dāng)△ACF周長取得最小值時，點F的坐標(biāo).

探究解析

上述是一道拋物線與三角形相結(jié)合的綜合題，共分三問，第（1）問為常規(guī)的求拋物線的解析式，后兩問則是關(guān)于三角形的屬性問題. 第（2）問給出了兩個三角形的面積關(guān)系，求直線斜率k的值，顯然考查的重點是拋物線中面積模型的構(gòu)建方式;第（3）問則構(gòu)建了△ACF，探究其周長取得最小值時點F的坐標(biāo)，實則為線段最值問題，考查拋物線中三角形的周長轉(zhuǎn)換及最值分析. 下面逐問分析，探究解題過程.

1. 聚焦曲線，待定系數(shù)破解

第（1）問求拋物線的解析式，核心解法是待定系數(shù)法，題目中給出了拋物線的頂點坐標(biāo)M（1，-4），可將其解析式設(shè)為y=a（x-1）2-4，將點C（0，-3）代入解析式中，可直接解得a=1，所以拋物線的解析式為y=x2-2x-3.

深究 可將拋物線解析式變形為y=（x-3）（x+1），根據(jù)該式可直接確定拋物線與x軸的兩個交點A和B的坐標(biāo)，即點A（-1，0），B（3，0）.

2. 關(guān)注面積，等高公式破題

第（2）問探究面積條件下直線斜率k的取值，基本思路是基于面積模型構(gòu)建關(guān)于參數(shù)k的方程，需要關(guān)注△BDE和△ADE的特點，即兩個三角形具有共同的邊DE，若將其視為三角形的底，則可將面積關(guān)系轉(zhuǎn)化為底邊上的高的關(guān)系，無須求面積.

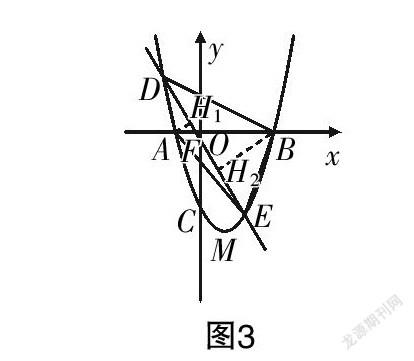
分別過點A和B作DE的垂線，設(shè)垂足分別為點H和H，如圖3所示. 則可將兩個三角形視為有公共底DE，高分別為AH和BH，結(jié)合面積公式可知，當(dāng)S=5S時，可得BH=5AH. 進一步分析可知△AFH∽△BFH，則兩個三角形的相似比為1∶5，可知BF=5AF. 又知A（-1，0），B（3，0），可推得點F的坐標(biāo)為

深究 問題突破的核心是轉(zhuǎn)化出“BF=5AF”，上述綜合了面積公式和三角形相似比. 若利用“鉛垂模型”來分析本問題，則可直接得出結(jié)論. 從“鉛垂角度”看待△ADE，則底為AF，點D和E在y軸方向的距離為鉛垂高;同理可知△BDE的底為BF，點D和E在y軸方向的距離為鉛垂高. 顯然兩個三角形的鉛垂高相等，當(dāng)S=5S時，可直接得出BF=5AF，無須借助三角形相似進行推導(dǎo). 兩種方法的轉(zhuǎn)化思路雖不同，但其核心思想是一致的，均圍繞“化斜為直”來進行構(gòu)建.

3. 深入周長，最值模型突破

最后一問是關(guān)于周長最值的問題，由周長公式可知其實質(zhì)是線段和的最值問題. 問題共分兩部分：第一部分求周長的最小值;第二部分確定點F的坐標(biāo).

深究 上述在求點F的軌跡時采用了代數(shù)計算法，通過參數(shù)間的運算來完成. 而求最值時引入了“將軍飲馬模型”，通過對稱轉(zhuǎn)化來確定最值情形. 線段最值問題的難點是對動點軌跡的確定，實際解析時也可從圖形特征入手，利用一些聯(lián)動模型來加以確定.

反思總結(jié)

上述綜合題的后兩問是核心之問，分別探究拋物線背景下三角形面積關(guān)系、三角形的周長最值，其解法和思路具有一定的特點，下面深入反思.

1. 面積關(guān)系探討

上述面積問題可歸為面積倍分關(guān)系問題，破解的基本策略是“等積變形+線段轉(zhuǎn)換”，即在圖形中探尋直線，利用等底等高來變形三角形頂點，然后將面積倍分關(guān)系轉(zhuǎn)化為線段關(guān)系. 線段轉(zhuǎn)化可借助三角形相似比，也可利用三角形“鉛垂”模型. 對于面積最值問題，基本策略是將其轉(zhuǎn)化為關(guān)于面積參數(shù)的函數(shù)，在自變量的取值范圍內(nèi)，利用函數(shù)的單調(diào)性來求其最值. 而對于面積定值問題則可進行等面積轉(zhuǎn)化，利用面積模型構(gòu)建對應(yīng)方程.

2. 周長最值探討

上述第三問為周長最值問題，本質(zhì)上實為線段和最值問題，因含有動點而增加了問題的難度，但突破的核心思路是一致的，即引入“將軍飲馬”模型，結(jié)合對稱轉(zhuǎn)換、共線原理求解. 線段最值的動點個數(shù)也是不確定的，對于單動點問題，通過一次對稱即可構(gòu)建三點共線，而雙動點（一定兩動）問題，則需要通過兩次對稱來實現(xiàn). 另外還可拓展到含系數(shù)的線段和問題上，問題解析需優(yōu)先處理其中的系數(shù)，可采用“取長補短”、倍分轉(zhuǎn)化等策略，后續(xù)可將問題轉(zhuǎn)變?yōu)槌Ｒ?guī)的線段和問題.

關(guān)聯(lián)拓展

上述總結(jié)了拋物線中三角形屬性問題的破題思路，下面結(jié)合一道關(guān)聯(lián)考題進行深入探究，強化解題策略.

問題 如圖5，已知拋物線y=ax2+bx+c與x軸交于點A和B（3，0），與y軸交于點C（0，-3），其對稱軸為x=1. 拋物線的頂點為D.

（1）求拋物線的解析式;

（2）分析拋物線的對稱軸上是否存在一點P，使得△PAC的周長最小？若存在，求出點P的坐標(biāo);若不存在，請說明理由.

（3）點E為BC上的一點，過點E作x軸的垂線，與拋物線的交點為F，試求△BCF面積的最大值.

解析 （1）簡答，由條件可知拋物線的解析式為y=x2-2x-3.

（2）點P位于拋物線的對稱軸上，△PAC的周長為PA+PC+AC，其中AC為定值，則只需求PA+PC的最小值，符合“將軍飲馬”模型，而點B是點A關(guān)于對稱軸x=1的對稱點，故無須作對稱點. 當(dāng)點B，P，C三點共線時線段和最小. 通過直線相交可得點P的坐標(biāo)為（1，-2）.

（3）根據(jù)題干信息可作圖6，線段EF將△BCF分割為兩部分，且點B和C是定點，符合“鉛垂”模型的構(gòu)建方法，EF可視為“鉛垂底”，點B和C的水平距離視為“鉛垂高”，則可將△BCF的面積表示為S=·EF·

評析 上述同為拋物線背景下的三角形面積屬性問題，其中求三角形周長最小值時同樣結(jié)合了“將軍飲馬”模型來轉(zhuǎn)化問題，而模型的方法原理是學(xué)習(xí)的關(guān)鍵. 題目中的三角形面積的最值問題，采用“鉛垂”模型來構(gòu)建面積函數(shù)，由函數(shù)性質(zhì)來求最值，理解“鉛垂”模型的高和底是關(guān)鍵.

總結(jié)思考

周長與面積是三角形的屬性，也是初中數(shù)學(xué)研究的關(guān)鍵內(nèi)容，將其與拋物線相結(jié)合，賦予其“數(shù)”與“形”的特性，則數(shù)形結(jié)合是重要的破題方法，探究學(xué)習(xí)中需要關(guān)注以下兩點.

關(guān)注點1：關(guān)注“點坐標(biāo)”的橋梁作用，拋物線中的三角形問題與常規(guī)幾何問題最大的區(qū)別是融合了曲線，而解析式賦予了曲線代數(shù)屬性. 問題解析需要建立如下轉(zhuǎn)換思路：“解析式?點坐標(biāo)?線段長或距離?面積或周長”，即利用點坐標(biāo)可推導(dǎo)三角形的屬性，同時可逆推求直線或曲線的解析式，這也是待定系數(shù)的方法體現(xiàn).

關(guān)注點2：關(guān)注圖像中的模型，拋物線與幾何問題的圖像較為復(fù)雜，問題突破要關(guān)注其中的模型，通過圖形拆解提取模型，從而有針對性地分析問題、構(gòu)建思路. 具體分析時建議采用數(shù)形結(jié)合的策略，結(jié)合題干信息理解圖形，把握圖形特征來轉(zhuǎn)化條件.