一道試題的探究與推廣

重慶市銅梁二中 (402560) 李 波 禇曉渝

題目已知拋物線C:y2=2px(p>0)過點M(m,2)為其焦點為F，且|MF|=2.

(1)求拋物線C的方程；

(2)設E為y軸上異于原點的任意一點，過E作不經過原點的兩條直線分別與拋物線C和圓F:(x-1)2+y2=1相切于點A,B，證明：A,B,F三點共線.

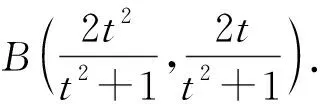
1 縱向探究

解析幾何題目往往是某個一般規律的特例，這就要求我們不僅要會解題，更要求根溯源，揭示一般規律.上題中的圓F是以焦點F為圓心且與拋物線C相切的圓，經過探究，得到下面的結論.

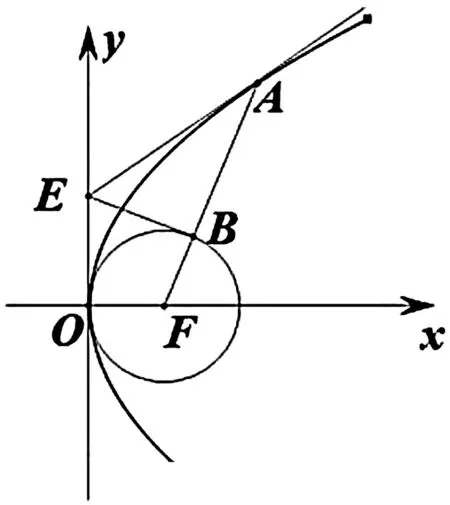
圖1

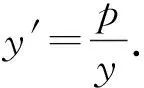
2 橫向類比

下面將性質1推廣到橢圓上得到了更加優美的性質.

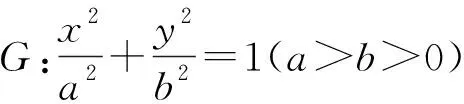
圖2

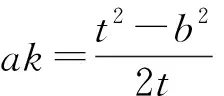
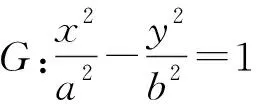
三 進一步的探究

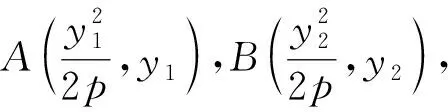
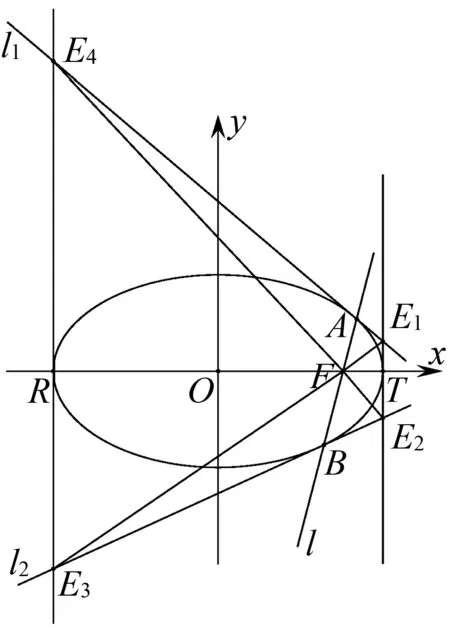
圖4

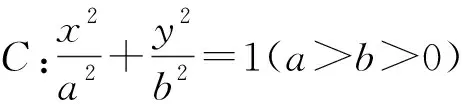
(1)E1,E2的縱坐標之積為-(a-c)2且△E1FE2為直角三角形；

(2)E3,E4的縱坐標之積為-(a+c)2且△E3FE4為直角三角形；

(3)E1,F,E3共線，E2,F,E4共線；

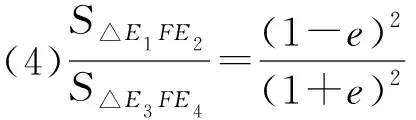
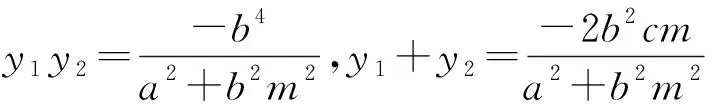
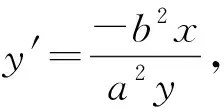
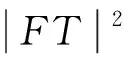
(2)類似于(1)的證明.

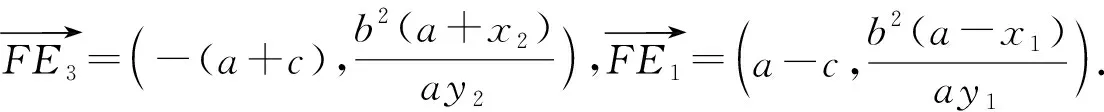
同理可證：E2,F,E4共線.

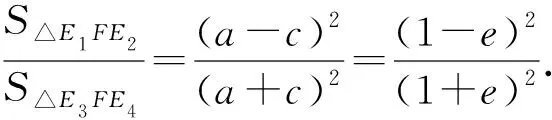
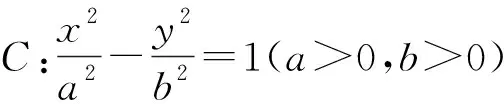
(1)E1,E2的縱坐標之積為-(a-c)2且△E1FE2為直角三角形；

(2)E3,E4的縱坐標之積為-(a+c)2且△E3FE4為直角三角形；

(3)E1,F,E3共線，E2,F,E4共線；

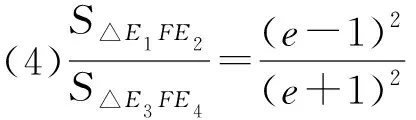
利用性質3和性質5，可以得到下面的結論.

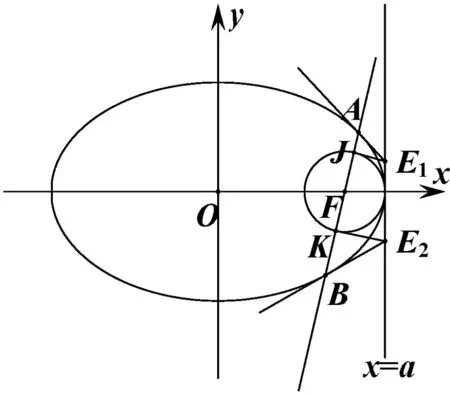
圖5