淺談如何培養(yǎng)利用線段圖解決百分?jǐn)?shù)應(yīng)用題

金亮

摘要：百分?jǐn)?shù)是小學(xué)數(shù)學(xué)六年級(jí)上冊(cè)一個(gè)重要的知識(shí)點(diǎn)，在生活中有著廣泛的應(yīng)用，因此學(xué)會(huì)運(yùn)用百分?jǐn)?shù)解決日常生活中的實(shí)際問(wèn)題有著重要的意義。在百分?jǐn)?shù)的學(xué)習(xí)中，學(xué)生對(duì)百分?jǐn)?shù)的意義以及與分?jǐn)?shù)小數(shù)的互化，和一些簡(jiǎn)單的計(jì)算比較容易掌握，但是到了用百分?jǐn)?shù)解決生活中的實(shí)際問(wèn)題時(shí)，不少學(xué)生卻遇到困難，解題思路不清晰。本文重點(diǎn)談?wù)摰氖侨绾卫脠D示法（線段圖），來(lái)加強(qiáng)孩子對(duì)百分?jǐn)?shù)應(yīng)用題的理解，理清思路。并且分析如何培養(yǎng)學(xué)生自己畫(huà)線段圖的能力，加深理解，分析如何提高學(xué)生的作圖能力、培養(yǎng)學(xué)生的作圖意識(shí)。

關(guān)鍵詞：百分?jǐn)?shù)、圖示法、單位“1”

中圖分類號(hào)：A 文獻(xiàn)標(biāo)識(shí)碼：A

一、論如何利用作圖轉(zhuǎn)換（簡(jiǎn)化）解題思路

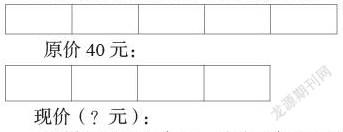
我們先從最簡(jiǎn)單的生活問(wèn)題入手，如一件商品原價(jià)40元，優(yōu)惠時(shí)全場(chǎng)八折，求該商品現(xiàn)價(jià)多少元，一般學(xué)生在解決此類問(wèn)題時(shí)會(huì)把原價(jià)看作單位“1”，原價(jià)已經(jīng)知道了，求它80%是多少，而求一個(gè)數(shù)的幾分之幾用乘法，所以學(xué)生們可以馬上列出算式：40×80%=32（元）

如果畫(huà)線段圖，現(xiàn)價(jià)是原價(jià)的80%，那也就是說(shuō)現(xiàn)價(jià)是原價(jià)的，用比的知識(shí)來(lái)理解就是現(xiàn)價(jià)和原價(jià)的比是4比5，所以畫(huà)圖時(shí)原價(jià)的長(zhǎng)度是5，現(xiàn)價(jià)的長(zhǎng)度是4。

這樣的圖畫(huà)出來(lái)后，就連三年級(jí)的學(xué)生都會(huì)做了，將原價(jià)平均分成5份，取其中的4份，用40÷5×4=32（元），六年級(jí)的話可以直接乘分?jǐn)?shù)：40× =32（元）

另外一種實(shí)際情況，一件商品原價(jià)50元，現(xiàn)價(jià)比原價(jià)便宜了三折，求現(xiàn)價(jià)是多少，其實(shí)該問(wèn)題與上題類似，都屬于知道原價(jià)求現(xiàn)價(jià)，只是說(shuō)法不同，便宜了三折，也就是相當(dāng)于打了七折，學(xué)生也很快能理清思路：50×（1-30%）=35（元）

用圖示法依然是一樣的思路，首先分析現(xiàn)價(jià)和原價(jià)的數(shù)量關(guān)系，現(xiàn)價(jià)和原價(jià)的比是7比10，原價(jià)是10，現(xiàn)價(jià)是7。

當(dāng)兩條線的長(zhǎng)度關(guān)系知道后，只要知道了其中一條長(zhǎng)度，另一條的長(zhǎng)度也就出來(lái)了，用50÷10×7=35。或者直接50×=35。

這兩種題型都是屬于單位“1”已知，求它的幾分之幾。在教學(xué)時(shí)我一般習(xí)慣于將單位“1”稱之為一個(gè)“整體”，而“它的幾分之幾或百分之幾”稱之為“部分”。此類題型我就簡(jiǎn)單地稱之為“知道整體求部分”。

不過(guò)當(dāng)單位“1”未知時(shí)，學(xué)生在理解上可能就有些難度。

如一件商品打了八折后是24元，求它原價(jià)是多少，老師初次講解時(shí)一般會(huì)先選用解方程的辦法：將原價(jià)設(shè)為未知數(shù)，列出的方程為80%=24，通過(guò)解方程得出步驟為24÷80%=30（元）。那么通過(guò)方程發(fā)現(xiàn)，這種題型用的是除法。在單位“1”未知，已知它的幾分之幾是多少來(lái)求出單位“1”，我一般習(xí)慣于將此種題型稱之為“知道部分求整體”。

但是因?yàn)檫@是從方程過(guò)程推導(dǎo)過(guò)來(lái)的，印象不會(huì)太深，學(xué)生不太明白其中的原理。那么該題型不能用線段圖來(lái)解釋原理嗎？肯定可以而且很簡(jiǎn)單，打八折表示現(xiàn)價(jià)和原價(jià)的比是4比5，已知的是現(xiàn)價(jià)24元，用圖像具體描述就是：

這樣一觀察，思路就特別清晰了，24÷4×5=30（元），或者24×。學(xué)生通過(guò)這樣的線段圖，印象毫無(wú)疑問(wèn)更加深刻，因?yàn)檫@是自己直觀看到并分析出的解題原理。

在百分?jǐn)?shù)應(yīng)用題中也存在一種“部分”比“整體”還多的情況，如某公司今年盈利180萬(wàn)元，比去年增長(zhǎng)了20%，問(wèn)去年盈利多少。六年級(jí)解題步驟是180÷（1+20%）=150萬(wàn)元。

那如果用線段圖解釋原理呢：題干里說(shuō)增長(zhǎng)了20%，也就是比去年增長(zhǎng)了，今年就相當(dāng)于去年的，今年和去年的線段長(zhǎng)度比就是6比5，已知今年盈利是180萬(wàn)元，所以用線段圖描述就是：

這樣的兩條線段圖畫(huà)出來(lái)之后，我們就知道用180÷6×5=150，或者直接180×=150，如果和前面那些題作比較就不難發(fā)現(xiàn)：不論是“知道整體求部分”還是“知道部分求整體”在原理上都可以用乘法來(lái)解題，也就是說(shuō)這兩種常見(jiàn)的題型如果利用線段圖轉(zhuǎn)換一下思路就是同一種題型了，都是“求一個(gè)數(shù)的幾分之幾是多少”。

二、如何引導(dǎo)學(xué)生畫(huà)線段圖

要如何培養(yǎng)學(xué)生的作圖能力，我覺(jué)得首先在課堂教學(xué)上，在遇到某些能夠利用作圖來(lái)講解的題時(shí)，就要有意識(shí)的利用作圖來(lái)給學(xué)生講解，讓學(xué)生明白用作圖能理清思路。第二點(diǎn)就是一定要讓學(xué)生自己動(dòng)手作圖，加深理解。

經(jīng)過(guò)一年度的觀察，我發(fā)現(xiàn)有學(xué)生將這種解題思路利用得很好，甚至有部分能力強(qiáng)的學(xué)生遇到問(wèn)題時(shí)，不用動(dòng)筆就能在腦海里構(gòu)建出一幅圖來(lái)。可以說(shuō)利用線段圖解題，不光是培養(yǎng)了他們的作圖能力，也鍛煉了他們的思維和想象力。簡(jiǎn)單的說(shuō)就是要做到教師多引導(dǎo)、學(xué)生多練習(xí)、教師及時(shí)評(píng)價(jià)，長(zhǎng)此以往，必定會(huì)有明顯的效果。

參考文獻(xiàn)

[1]趙寶田.線段圖在低段數(shù)學(xué)教學(xué)中的有效運(yùn)用[J].中小學(xué)教學(xué)研究，2011（05）.

[2]梁崎.從問(wèn)題解答到解決問(wèn)題的轉(zhuǎn)變———淺談人教版小學(xué)數(shù)學(xué)教材對(duì)應(yīng)用題教學(xué)的改革[J].小學(xué)教學(xué)參考，2011（23）.