立足構圖 分類突破

邵樂華

[摘 ?要] 剛復習完某知識，學生面對考查此知識的復雜問題時卻無從下手，這種現象經常出現. 文章以一道期末試卷壓軸題為例，采用一定的教學手段，引導學生走出解題困境，并從中積累解題經驗，促使他們提升數學核心素養.

[關鍵詞] 壓軸題;初中;教學;反思

在一次期末考試中，有一道壓軸題，許多學生感到棘手，能全做對的學生少之又少. 剛復習完與此題相關的知識，為什么學生會一籌莫展呢？筆者對此題進行了認真研究，并思考了如下問題：如何引導學生走出解題困境？如何從中抽出基本幾何模型？如何從中提煉基本數學思想方法？如何讓學生從中積累解題經驗，進而促進學生核心素養的提升？

原題再現

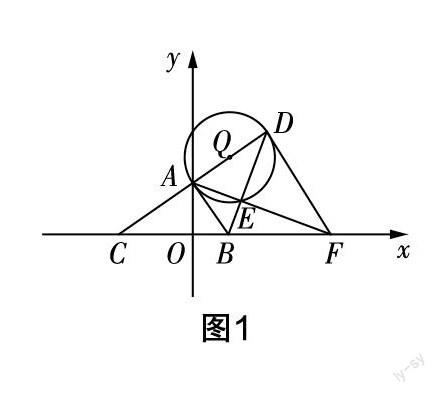
原題如圖1所示，在平面直角坐標系xOy中，已知A（0，4），點B是x軸正半軸上一點，連接AB，過點A作AC⊥AB，交x軸于點C，點D是點C關于點A的對稱點，連接AD，BD，以AD為直徑作☉Q交BD于點E，連接AE并延長交x軸于點F，連接DF.

（1）求證：AE=AO;

（2）若AB-BO=2，求tan∠AFC的值;

（3）若△DEF與△AEB相似，求EF的值.

此題以平面直角坐標系為背景，把圓與三角形進行有機結合，考查全等三角形的判定與性質、相似三角形的判定與性質、勾股定理、銳角三角函數、等腰三角形的判定與性質、圓周角定理等數學主干知識. 同時，要求學生運用轉化思想、數形結合思想、方程思想、分類討論思想、模型思想解決問題. 其中第（2）題求tan∠AFC的值思維含量比較高，學生需要利用相似三角形的性質，逐步轉化線段的比;第（3）題求EF的長，需要分類討論，且每一種情況都需要找到與線段EF相等的線段. 那么解決此題，應如何構圖、如何轉化呢？有何規律？

解題教學

著名數學家華羅庚指出，解題退到最原始的狀態，是解決問題的一個訣竅. 最原始的狀態是什么呢？就是原題中的關鍵詞，包括圖形中的點與線段，圖形的相對位置關系與數量關系，代數的特征與圖形的對稱性等，這些是數學思維的起點，既能促使解題思路自然形成，又揭示了解題方案的形成過程. 如“AC⊥AB”“點D是點C關于點A的對稱點”“以AD為直徑作☉Q”都是試題的重要信息，是思維的起點.

1. 審題

審題是解題的首要環節. 教學中，教師應重視審題環節，應引導學生學會審題. 問題的結構形式可以分為兩種，一是并列式問題結構，即從原始題干出發，提出兩個或多個并列的問題;二是遞進式問題結構，即從原始題干出發，所提問題的難度不斷增加，解決前一個問題能為解決后一個問題奠定基礎.

2. 追本溯源

仔細品味這道題，會發現其基本素材源于教材的下面幾個內容：

①如圖2所示，AB是☉O的直徑，∠ABT=45°，且AT=AB，求證：AT是☉O的切線;

②如圖3所示，在Rt△ABC中，CD是斜邊AB上的高，求證：△ACD∽△ABC，△CBD∽△ABC;

③如圖4所示，AB=AC，∠A=40°，AB的垂直平分線MN交AC于點D，求∠DBC的度數.

命題人將教材的例、習題進行組合，把這些圖形放在同一個圖形中，并以平面直角坐標系為背景，將三角形、銳角三角函數與圓融合在一起. 對于原題的第（3）題，由于兩個直角三角形相似時，直角必須對應相等，所以只需要分兩種情況進行討論.

3. 解法分析

對原題進行解法教學時，教師可提出如下3個問題.

問題1：解決平面直角坐標系中的幾何問題時，應如何轉化條件？

（預設答案：把點的坐標轉化為對應線段的長，把斜放的直角三角形通過“改斜為正”轉化為“一線三直角”模型，利用兩坐標軸互相垂直構造直角三角形）

問題2：如何解決與圓相關的問題？

（預設答案：利用圓的性質，把有關圓的問題轉化為三角形或四邊形問題，然后利用三角形或四邊形的性質求線段的長或角度）

問題3：如何求某個銳角的三角函數值？未指明對應關系的兩個直角三角形相似，可能有幾種情況？

（預設答案：欲求某個銳角的三角函數值，必須把這個銳角放置在直角三角形中，轉化為直角三角形邊與邊的比. 當兩個直角三角形相似時，可能有兩種情況）

原題答案（1）因為點D是點C關于點A的對稱點，AB⊥AC，所以AB是線段CD的垂直平分線. 根據線段垂直平分線的性質，得BC=BD. 根據等邊對等角，得∠ACB=∠ADB. 又由條件易知∠BAC=∠BAD=90°，所以∠ABO=∠ABE. 因為AD是☉Q的直徑，根據直徑所對的圓周角是直角，得∠AED=90°. 所以∠AEB=90°. 因為∠AOB=∠AEB=90°，∠ABO=∠ABE，AB=AB，由角角邊定理，得△ABO≌△ABE. 所以AE=AO.

（2）由（1）知△ABO≌△ABE，所以∠OAB=∠EAB. 根據同角的余角相等，得∠OAB=∠ACF，所以∠EAB=∠ACF. 又∠AFB=∠AFB，所以△AFB∽△CFA. 所以=. 設BO=x，則AB=2+x. 在Rt△ABO中，由勾股定理，得AB2=AO2+BO2，即（x+2）2=42+x2，解得x=3. 所以BO=3，AB=5. 所以tan∠ACF===. 設BF=3y，則AF=4y. 在Rt△AOF中，由勾股定理，得AF2=AO2+OF2，即（4y）2=42+（3y+3）2，解得y=或y=-1（不合題意，舍去）. 所以BF=，OF=. 在Rt△AOF中，由正切函數的定義，得tan∠AFC===.

（3）分兩種情況討論：①當△DEF∽△BEA時，∠BAE=∠DFE，所以AB∥DF. 所以∠ADF=∠CAB=90°. 過點F作FN⊥x軸，過點D作DM⊥y軸交y軸于點M，DM與FN交于點N，如圖5所示，則四邊形MNFO為矩形，∠DMA=∠COA=90°. 因為∠MAD=∠OAC，DA=CA，根據角角邊定理，得△DMA≌△COA. 所以AM=AO=4，∠MDA=∠OCA. 因為∠ACB=∠ADB，所以∠MDA=∠ADB. 根據等角的余角相等，得∠FDE=∠FDN. 因為FE⊥BD，FN⊥MN，根據角平分線的性質，得EF=FN=OM=8. ②當△DEF∽△AEB時，∠FDE=∠BAE. 根據同角的余角相等，得∠BAE=∠ADB，所以∠ADB=∠FDE. 由等角的余角相等，得∠DAF=∠DFA. 所以AD=DF. 因為DB⊥AF，根據等腰三角形三線合一，得EF=AE=4. 綜上所述，若△DEF與△AEB相似，EF的值為4或8.

評注解決第（2）題時，上述解法用到了兩個相似模型，一是射影定理模型;二是反“A型”相似模型. 求線段長度時用到了兩種基本方法，一是利用勾股定理建立方程求線段的長;二是利用相似三角形對應邊成比例求線段的長. 在進行等比轉化時，利用的是等角轉化. 解決第（3）題時，上述解法首先應用分類討論思想，把一個復雜的問題分解為兩個小問題：△DEF∽△BEA與△DEF∽△AEB. 解決△DEF∽△BEA時，構建了“一線三直角”幾何模型;解決△DEF∽△AEB時，構建了等腰三角形基本圖形.

4. 模型、方法提煉

（1）全等模型

軸對稱型：△AOB≌△AEB，△ACB≌△ADB，△EDF≌△NDF;

中心對稱型：△AOC≌△AMD.

（2）相似模型

“三垂直”模型：△AOC∽△BOA∽△BAC;

“反A型”模型：△ABF∽△CAF;

“X型”模型：△AEB∽△FED，△AEB∽△DEF;

“一線三直角”模型：△MAD∽△NDF.

（3）特殊三角形模型

等腰三角形BCD，等腰三角形ADF，直角三角形ABC，直角三角形AOC，直角三角形AOB，直角三角形AED，直角三角形AOF，直角三角形MAD，直角三角形DNF等.

（4）運用勾股定理

在直角三角形中，已知一邊及另外兩邊的關系，可以利用勾股定理求其他兩邊的長.

（5）等角對等比

比如，當∠OAB=∠ACF時，tan∠OAB=tan∠ACF.

5. 鞏固提升

教學此題后，為了讓學生鞏固其中運用的知識、方法與技巧，教師可設計如下試題供學生練習.

（1）如圖6所示，AB為☉O的直徑，C，D是☉O上的兩點，AC=BC，AD的延長線與CB的延長線交于點E. 若∠DAB=20°，求∠E的度數.

（2）如圖7所示，AB是☉O的直徑，D是☉O上一點，DE是☉O的切線，過點B作BF⊥DE，垂足為F，分別延長AD，BF交于點C.

①求證：∠A=∠C;

②當BF=1，DF=2時，求☉O的直徑.

（3）如圖8所示，☉O是矩形ABCD的外接圓，∠ABC的平分線分別交AC，☉O，CD的延長線于點E、點F和點G，過點F作☉O的切線FH交CG于點H.

①求證：FH∥AC;

②若BA=BE，tan∠BAC=3，OE=2，求FH的長.

教后反思

1. 立足圖形構造，為學生排憂解難

由于個體差異，學生解決同一問題時所出現的問題也有所不同，或知識斷層，或沒有發現隱含條件，或計算失誤等. 教學中，教師應引導學生分步踩點得分，加強基本圖形的構造，促使學生整合條件，利用圖形思考與探究，進而把握解題的正確方向.

2. 加強變式練習，拓展思維空間

數學家希伯特指出，當解決一個問題時，一系列的新問題也隨之誕生，當解題成功時，要善于提出新問題. 因此，教學中，教師不能就題論題，應深入領悟典型試題的編寫意圖，通過一題多解、一題多問、一題多變、多題一解等拓展學生的思維空間. 如本題就進行了一題多問、一題多變，使習題教學從淺層走向深層.

3. 關注思想方法，提升學生素養

數學思想是數學知識與方法的高度概括. 在教學中，教師應注重數學思想方法的提煉與滲透，從而提升學生的核心素養. 如本題教學滲透了轉化思想、數形結合思想、方程思想及分類討論思想.