基于深度學習 重拾教材碎片

[摘? 要] 初中數學教學中，受學生思維力和知識儲備等因素的限制，會遺留知識碎片.教師基于深度學習理念，在整體理解課程和精準評估學情的基礎上，重拾碎片，設計融合章節的大單元教學，讓學生在深度學習中發展核心素養.

[關鍵詞] 深度學習;教材碎片;核心素養;單元整體

受學生的思維力和知識儲備等因素的限制，在數學教學中，不可避免地會遺留一些知識碎片，給學生設置了“知其然，不知其所以然”的認知門檻. 知識的零散與斷層，讓部分學生難以把握數學的整體結構，使教學陷于淺層次、低效率的困境. 初中數學深度學習要求能夠整體呈現初中數學內容的結構，以融會貫通的方式對學習內容進行組織、整合[1]. 教師基于這一理念，在學生思維力和知識儲備達到要求時，重拾教材碎片，跨章節融合教材，貫通式設置教學環節，形成有思維場的大單元教學，為學生搭建學習階梯，使學生在解決問題的情境中，達成構筑知識體系，實現思維進階，發展核心素養的教學目標.

問題提出

1. 問題背景

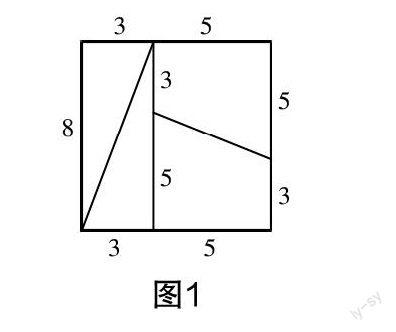
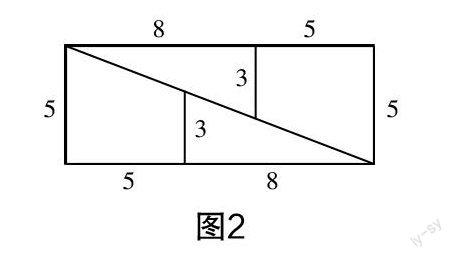
圖1和圖2是蘇科版七下第12章“證明”的章頭圖.

原文：圖1是面積為64的正方形紙片，把它剪成4塊，按圖2所示重新拼合，這4塊紙片恰好能拼成一個長為13、寬為5的長方形嗎？

2. 教材思考

該章頭圖旨在通過拼合圖形，給學生營造出將面積為64的正方形拼成了面積為65的長方形的“神秘”情境，激發學生的學習興趣，在教師的引導下，通過操作、觀察和思考，尋找“面積多出1”的原因，感知該“神秘”情境的不合理性. 讓學生認識到通過思考、觀察、操作、實驗得到的結論不一定是正確的，為學生種下追求真理的種子，感受證明的合理性與必要性，揭開章節學習的序幕，實現從合情推理到演繹推理的交融過渡.

該章頭圖雖然培養了學生的問題意識，激發了學習興趣，但數學的核心是解決問題，僅發現、提出問題，沒有分析、解決問題，知識生長鏈條不完整. 而以七年級學生的知識儲備與思維層次，的確較難找到面積相差1的說理方法，通常是教師給出“矩形的中間有空白”、“不能拼成長、寬分別為13和5的矩形”等解釋，學生的印象不深刻，對知識的理解浮于表面，隨著時間的推移，較多的學生容易淡忘. 該圖在七年級的教學中，雖發揮了啟后的作用，卻以“碎片”的形式遺留，在某種程度上限制了學生的思維進階.

通觀蘇科版初中數學6冊教材，該圖沒能如“搭小魚”等情境，隨著學生思維進階與知識儲備增多而漸次呈現. 該章頭圖雖為學生埋下了思維的種子，卻沒能催生、成長，留白過大，給學生設置了“知其然，不知其所以然”的認知門檻.

教學實施

1. 設計原則

學生的思維水平與知識儲備是決定能否有效開展數學深度學習的條件之一. 蘇科版數學教材八年級上冊第五章和第六章分別為平面直角坐標系和一次函數，筆者在結束上述兩章的教學后，基于深度學習的理念，審慎學情，以重拾教材碎片設置問題情境，融合章節實現大單元教學，學生在深度學習中發展核心素養為原則，設計并實施了以“1從哪里來？”為題的單元教學.

2. 教學片段呈現

師：同學們，七年級時，我們曾接觸了這樣一個問題，圖1是面積為64的正方形紙片，把它剪成4塊，按圖2所示重新拼合，這4塊紙片恰好能拼成一個長為13、寬為5的長方形嗎？組成正方形的4個圖形分別是哪些圖形，它們之間有什么關系？

生：我發現有兩個全等的直角三角形，和兩個全等的直角梯形.

師：可以用什么方法驗證這位同學的猜想？

生：用疊合法可以驗證，兩個直角三角形和兩個直角梯形是對應全等的.

師：怎樣拼合這4個圖形，形成如圖2所示的矩形？

生：直角三角形的較短直角邊和直角梯形的上底長度相等，所以分別用將直角三角形和梯形組合，可分別形成兩個較大的直角三角形，然后將兩個大直角三角形重合斜邊可組成如圖2所示的矩形.

師：請同學們動手試一試.

學生完成后，展示拼成的矩形.

師：請同學們計算拼成的矩形面積是多少？

生：矩形的面積計算公式是長乘以寬，拼成后的矩形長為13，寬為5，所以面積是65.

師：比較正方形和矩形的面積，同學們有什么發現？

生：老師，我發現面積由64變成了65，這真的很神奇.

師：這種神奇的現象真實存在嗎？

生：我認為存在，通過計算可以獲得，圖形的面積確實發生了改變.

（教室中略安靜，隨后有學生小聲議論.）

生：我不認同這個觀點，我感覺面積不可能由64變成65，因為圖形面積是守恒的，重新組合只是形狀發生了變化，面積是不可能改變的.

生：我記得在七年級時，老師說過這個問題，面積是不會變的，不可能由64變成65.

師：但是同學們通過計算的確發現了面積多了1，1從哪里來？觀察你手里的拼圖，想一想原因.

（學生觀察、動手、思考.）

生：我認為面積不可能多1，但是我沒找到合理的解釋.

生：我剛才在擺動矩形的過程中，發現矩形的對角線好像沒能完全貼合，不知道是不是我裁剪的過程中有誤差.

有學生附和也發現了這一現象.

師：同學們，如何來驗證對角線不在一條直線上呢？

生：可用平角，因為平角是180°，利用特殊角可以證明.

師：你的思路很好，能想到從形的角度來解決這個問題，說說你的具體思路.

生：四個圖形除直角外，其他角度都不明確，不能完成證明.

師：這位同學雖然沒給出具體的思路，卻提供了一條有價值的線索，即我們所看到的對角線可能不在同一條線段上，可以怎樣來說理呢？

生：我想可以在對角線上取3個點，過兩點確定一條直線，如果第三點在直線上，則三點共線，如果第三點不在該直線上，則三點不共線.

師：直線是外顯的形，結合近期所學，由直線你能想到什么？

生：一次函數的圖像.

教師：很好，現在有這么多的線索了，能理出什么樣的思路？

生：建立坐標系，讓矩形左下頂點與原點重合，相鄰的長和寬與坐標軸重合，根據題中的數據，能得出矩形兩個頂點的坐標，用待定系數法求出該一次函數表達式，然后在“對角線”上再找1個點的坐標，就能驗證這三點是否共線.

師：這位同學說的很細致，請同學們快速求解，我請一位同學上來展示過程.

（教師指定一名學生板書過程，完成板書后向其他學生口述解題思路.）

師：由三點不共線，可得到哪些結論？

生：可驗證，矩形中間確實有空白.

生：我知道面積為什么會相差1了，因為中間有空白，四個圖形在組成矩形時，并不是完全對接的，我感受到另一種證明方法.

師：在獲得這一結論的過程中，同學們用了哪些方法，有什么感悟？

生：建立坐標系，將圖形問題轉化為代數問題，實現了數形結合.

生：以后見到直線，可以考慮能否建立一個合理的坐標系，然后用表達式描述直線.

師：同學們說得很好，理性思維是數學的核心，觀察、操作得到的結論不一定正確，只有通過證明得出的結論才是正確的，課后請繼續思考其他解法.

教學反思

1. 融合教材碎片，形成單元教學

教材是詮釋《課標》的載體，解讀課標并合理分解到章節，在課標、教材及學情間建立融通共生的渠道，需要教師從整體上把握教材的價值，催生其教與學的最大效能. 該章頭圖在七年級教學中，雖然發揮了幫助學生認識證明必要性的效能，但限于學生的認知水平，當時較難找到證明的思路，使認識浮于表面，沒能更大程度地挖掘該情境的價值. 《課標》指出：數學教學過程中恰當地使用數學課程資源，將在很大程度上提高學生從事數學活動的水平和教師從事教學活動的質量[2]. 在八年級上學期，學生學習了平面直角坐標系和一次函數后，積累了用解析法解決問題的經驗，有了重拾教材碎片，形成單元教學的基礎. 此時，基于深度學習的理念，融合了矩形的性質、平面直角坐標系、一次函數等知識，設計該教學內容，形成大單元教學鏈條，知識的綜合面廣，思維跨度大，在析粹解決問題的過程中，培養學生的理性思維，拉伸了學生的深度思考域.

2. 綜合運用知識，學生思維進階

問題既是數學新知的邏輯生長點，又是數學知識、技能與能力的邏輯發展點，也是數學活動的載體. 達成深度學習的元素是多元化的，但起決定性作用的依然是教師、教材和學生. 教師要客觀評價學情，對數學有深度的理解，既能設置合理的問題情境，又能找到解決問題的驅動力，組織學生在問題情境中獨立思考、合作交流，調用知識儲備，借鑒過程方法經驗，切準問題核心，梳理解題途徑，使學生在親歷解決問題的過程中，領悟從“學什么”到“如何用”的轉化過程. 本課例源于蘇科版七年級教材的碎片遺留，在深度學習理念的指引下，合理評估學情，將該章頭圖重現于八年級的教學中，在問題情境中學生綜合運用矩形、平面直角坐標系和一次函數的知識儲備，漸次轉化問題，逐步切準核心并最終解決問題，在大單元的教學過程中，達成了深度學習的目標，學生實現了思維進階，發展了數學核心素養.

3. “三會”思想統領，達成深度學習

史寧中教授對《高中數學課程標準（2017年版）》的六大數學核心素養解讀為“會用數學的眼光觀察世界，會用數學的思維思考世界，會用數學的語言表達世界. ”[3]三會思想突出反映了數學學科核心素養的本質. 本課例，筆者基于深度學習的理念，通過重拾教材碎片，在跨章節的融合中形成大單元教學，在探究的過程中，喚醒學生的求知欲望，在尋找解題思路中滲入數學思想方法，在問題解決的情境中實現學生思維進階，學生從拼成的矩形紙片中抽象出點、線，建立坐標系，經歷了“會用數學的眼光觀察世界”，探究得到用一次函數描述直線，判斷第三點是否在該直線上的求證思路，經歷了“會用數學的思維思考世界”，建立起一次函數的數學模型，并用以解決問題，經歷了“會用數學的語言表達世界”，整節課在“三會”思想的統領下，達成了深度學習的目標.

參考文獻：

[1] 劉曉玫，黃延林. 深度學習：走向核心素養[M]. 北京：教育科學出版社，2019.

[2] 中華人民共和國教育部. 義務教育數學課程標準（2011年版）[S]. 北京：北京師范大學出版社，2011.

[3] 吳曉紅，謝海燕. 基于學科核心素養的數學教學課例研究[M]. 上海：華東師范大學出版社，2019.

基金項目：江蘇省教育科學“十四五”規劃課題“基于核心素養的初中數學單元整體教學實踐研究”（D/2021/02/136）.

作者簡介：魏宇亭（1981—），本科學歷，中小學高級教師，從事初中數學教學工作，曾獲江蘇省優秀課一等獎，徐州市優秀課一等獎，徐州市帶頭優師，邳州市名師等獎項和榮譽.