一道圓錐曲線問題的探究與拓展

江蘇省常州高級中學 (213000) 黃龍孫 福建省廈門市海滄中學 (361022) 陳凌燕

圓錐曲線中有一類定點定值問題，是指在運動變化過程中，或動直線總是過某個定點，或交點總是在某條定直線上，或某個幾何量(線段長，面積等)總是一個定值，蘊含了變化中的不變性，給人以一種奇妙的數學美的感受.同時這類問題通常具有入口寬、方法多但又需要扎實的學科技能和素養才能得以解決，本文以一道圓錐曲線問題的探究和拓展過程來展示這種數學的處理方法.

1 試題呈現

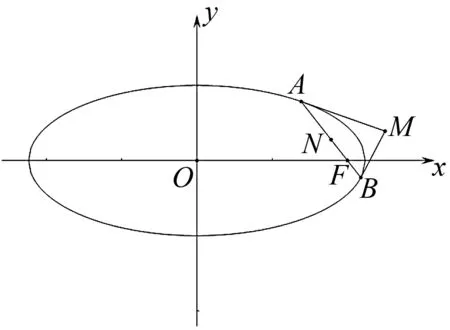
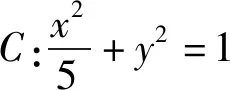
2 分析與解

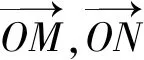
思路1：設AB直線方程，用直線方程的參數表示M，N兩點.因為AB在繞著右焦點F轉動的過程中，M，N兩點也隨之改變，所以M，N兩點的坐標與直線AB的位置有關，自然產生用直線AB方程的參數來表示的思路.

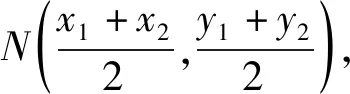
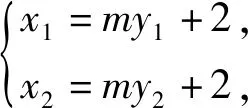
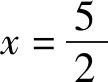
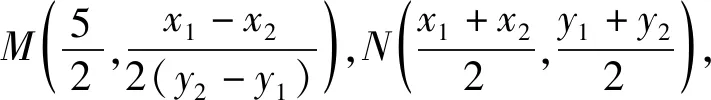
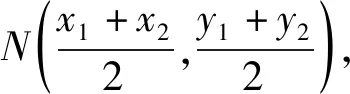
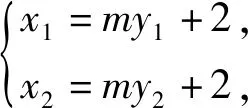
反思：從解法2過程來看，M,N的坐標直接用A,B的坐標來表示，省去了聯立直線AB方程與橢圓方程的過程，不僅運算量更小，過程更簡潔，同時也便于結論的推廣.可見，只需滿足AB是橢圓的動弦，中點為N，橢圓A,B處的切線相交于點M，則O，M，N三點共線.

3 探究拓展

解完題后我們用幾何畫板演示可以直觀地看到在AB變動的過程中，O，M，N始終三點共線，而且M點也一直在橢圓的準線上運動，同時更為簡潔的解法二也更具一般性，這讓我們感受到數學的奇異美和滿足感，以及繼續探究的躍躍欲試之感.

問題1：能否將交點M在定直線上推廣到一般橢圓上？

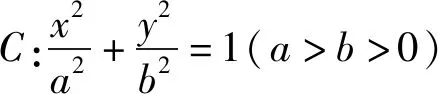
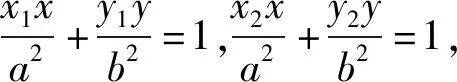
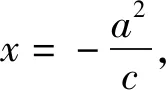
問題2：如果AB直線過的定點不是焦點，那么交點M會在定直線上嗎？直線方程是什么？

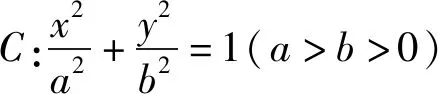
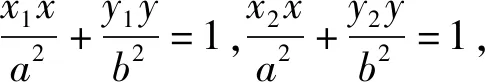
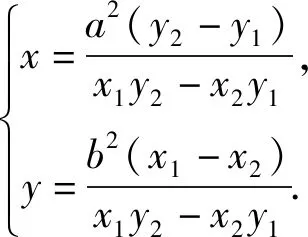
問題3：逆向思考，反之，如果已知定直線上的動點M向橢圓引切線，則兩切點所在的直線會過定點嗎？

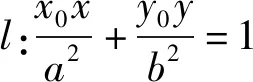
問題4：O，M，N三點共線能否推廣到一般橢圓上？

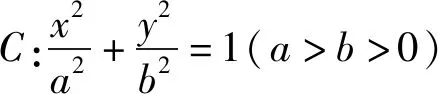
結論3、結論4證明略.

問題5：雙曲線和拋物線能否有類似的結論？

回答是肯定的，以下給出了課后學生探究得到的結論，此處篇幅所限，略去證明.

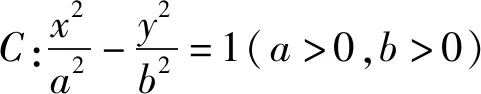
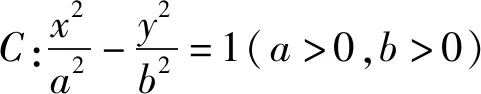
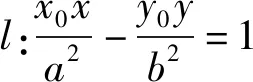
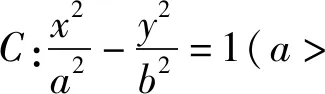
命題5 拋物線C:y2=2px(p>0)上一點A(x0,y0)處的切線方程為y0y=p(x0+x).

命題6 若AB是拋物線C:y2=2px(p>0)的動弦，且過定點(x0,y0) ，則拋物線C在A，B處的切線的交點M在定直線l:y0y=p(x0+x)上.

命題7 若M在定直線l:y0y=p(x0+x)上，過M作拋物線C:y2=2px(p>0)的切線，切點分別為A，B，則直線AB過定點(x0,y0).

命題8 已知AB是拋物線C:y2=2px(p>0)的動弦，中點為N，拋物線C在點A，B處的兩切線的交點為M，則MN∥x軸.

4 教學啟示

圓錐曲線問題具有很好的探究價值，一是不同的解法運算量和運算難度不同，找到一個簡潔的解法會產生很強的滿足感，二是蘊含著豐富的數學思想，例如特殊到一般，數形結合等，三是解完題后繼續將成果推廣到一般情形或者逆向思考，交換條件和結論研究逆命題等，能夠激發學生的好奇心和求知欲，讓學生的自主探究的過程中，掌握數學研究的方法，提高學科素養，領悟數學思想，并體會數學的奇異之美，真正享受學習數學的快樂！