電子信息類專業課程體系網絡分析研究
張衛濤 劉海濱 谷少行 郭輝
背景:本文基于網絡科學理論對高校電子信息類課程體系進行了詳細的研究分析。同時為這些科目的教學提供了一些建議。隨著網絡科學的研究不斷深入,利用網絡理論對課程體系進行分析有著重大的研究意義。
關鍵詞:復雜網絡;電子信息工程;電子科學與技術;課程體系;聚集系數;介數;平均路徑長度
1 電子信息類專業課程網絡建模
本文的對象是電子信息類專業課程體系,首先需要對電子信息類的專業課程網絡進行建模。因為電子信息類是個大類,它包括電子科學與技術、電子信息工程、通信工程。所以要把它們所有專業課程整合到一起。找到他們兩兩之間的出入關系,把所有的關系整理成csv文本形式。一共有36門課程、136個關系,36個節點,136條邊。
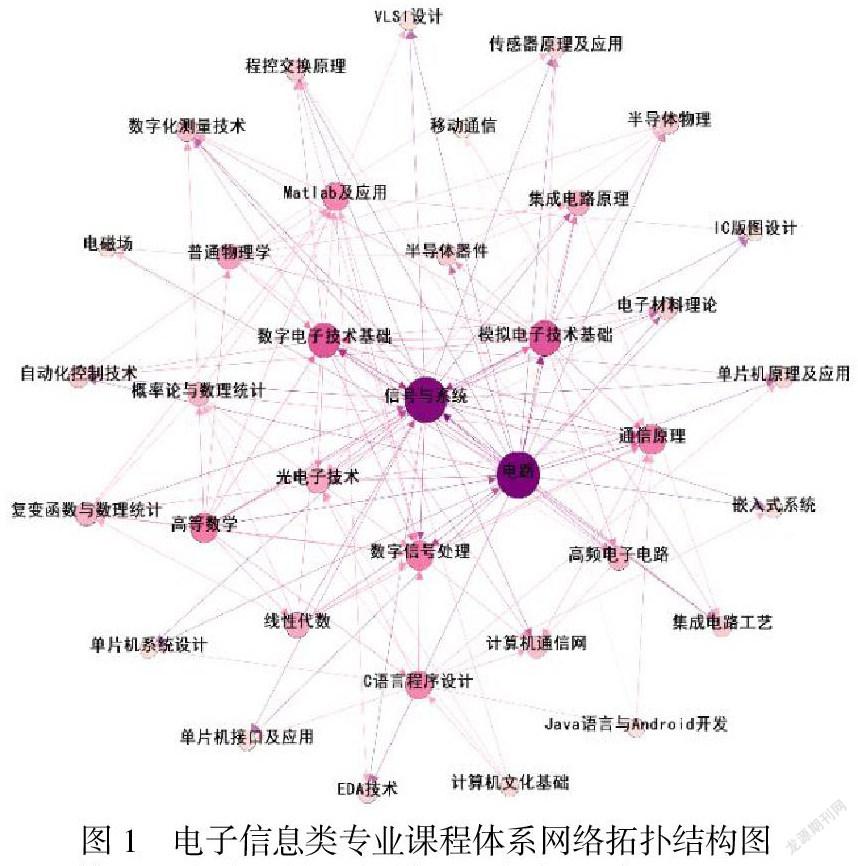
把用于表示課程關系的csv文本形式的電子表格數據資料導入Gephi可視化仿真軟件,得到了36個節點136條邊,我們對初步課程體系網絡進行了外觀和布局的細微調整,這樣做的目的是為了可以讓課程網絡看起來更直觀的展現。除此對節點進行了顏色添加規則設置,其添加顏色的規則為:如果節點度越大,其顏色俞深。節點的度越小,其顏色俞淺。另外我們還對網絡節點進行了視覺上的規則設置,規則為:如果節點的度的數值越大,那么該節點的視覺大小就越大。反之如果節點的度的數值越小,那么該節點的視覺大小就越小。為了更加清晰的顯示整個課程體系網絡拓撲結構,選用Fruchterman Reingold布局。和簡單的數據和蒼白的語言比起來,直觀上視覺(網絡拓撲結構圖)便于讀者直觀的分析網絡上的元素,如圖1所示。
2 基于網絡統計特性的結果分析與討論
2.1 基于節點度特性的網絡分析
度是復雜網絡中節點的一個重要屬性,簡單來說度是指與一個節點相連的邊的個數。大多數人們在刻畫復雜網絡結構的統計特性上提出了許多的概念和方法。例如節點的度定義為和該節點的連接邊數有關。我們可以更直觀的看出來某一個節點的度值越大,說明該個節點在某種意義上就越重要。因為本文的研究的目標是電子信息類專業課程,它們兩兩之間的的關系是由它們所應有的知識點的了解和學習來確定的,由于我們會發現無論哪兩個節點之間它們的連邊是有向的,本文的中的課程體系網絡為有向網絡。對有向網絡的理解,我們首先要了解出度和入度的概念。出度是從一個節點出發的邊數,而入度是指向一個節點邊的數目。
對建立的電子信息工程專業課程體系網絡模型的度值進行統計示,計算度值相對大的8門課程。節點的度大小直接反映該節點課程在體系網絡中的重要性,所以學習者應該將其對應課程作為重點學習對象。分別統計出了電子信息工程專業課程中入度和出度最大的5門課程,結果表明入度較大的五門課是技能型專業課,出度比較大的五門課多是數學類的公共基礎性課程。
2.2 基于聚集系數特性的網絡分析
通過Gephi軟件計算的得到整個課程體系的平均聚類系數和單個節點的聚類系數。平均聚類系數為0.265,單個節點的聚類系數。我們可以利用結論(當兩門課程之間的聚類系數遠大于該網絡的平均聚類系數時,這說明這兩門課程之間關聯比較密切)可以幫助教師在教學過程中可以對課程的設置的進行合理地安排,進而還可以提高教學效率,使學生學習更容易掌握的知識。
2.3 基于介數特性的網絡分析
介數是一個可以用來表示一個節點作為其他節點中間節點傳遞能力的統計特性。如果一門課程的節點介數越大,表示這門課程越重要,在復雜網絡中承接的作用就越大。所以在老師的教學和學生學習過程中,告誡大家,當學生對這門課程進行學習之前,應預習好該課程的先導課程,同時要學習好該門課程,其目的是為了該門課程的后備課程做好基礎性學習,打下扎實的基礎。假如這門課程在教學和學習過程中有不足的地方,會使整個學習網絡無法順利完成,影響的是全部網絡。所以要認真的去學習這門課程。
3 結語
本文以電子信息類本科專業課程包含的知識點、每個學科的教學大綱,教學要求為基礎,構建了一個以電子信息類課程體系網絡,該網絡以每門課程為節點,通過研究它們之間的知識點關聯建立有向邊,并利用網絡可視化Gephi這一分析工具進行了深入的研究分析。對一個網絡系統的拓撲結構的研究一般大體分為三個階段:首先是建模,接下來是仿真,實現網絡的可視化,最后是統計網絡特性,分析統計結果。最后將分析結果與專業課程的教學實際相結合,和高等院校教學課表相比較,提出對教學改革的建設性建議。不僅實現了對課程授課和學習順序的驗證及調整,也為當前的高等教育中的大類招生的教學改革提供了有效工具。
參考文獻:
[1]關迎暉,向勇,陳康.基于Gephi的可視分析方法研究與應用[J].電信科學,2013,29(S1):112-119.
[2]吳泓潤,覃俊,鄭波盡.基于代價的復雜網絡抗攻擊性研究[J].計算機科學,2012,39(08):224-227+255.
[3]王友忠,曾大軍,鄭曉龍,王飛躍.基于復雜網絡理論的互聯網新聞媒體分析[J].復雜系統與復雜性科學,2009,6(03):11-21.
[3]汪小帆,李翔,陳關榮.復雜網絡理論及其應用[M].北京: 清華大學出版社,2006.
[4] 劉濤, 陳忠, 陳曉榮.復雜網絡理論及其應用研究概述[J]. 系統工程, 2005, 23(6):1-7.
[5] 劉建. 復雜網絡及其在國內研究進展的綜述[J].系統科學學報,2009,17(4):31-37.
[6]俞桂杰, 彭語冰, 褚衍昌.復雜網絡理論及其在航空網絡中的應用[J].復雜系統與復雜性科學.2006,3(1):80-84.
[7]吳海峰.最短路徑算法——Dijkstra及Floyd算法[J].中國新通信,2019,21(02):32-33.
[8]姜雅文,賈彩燕,于劍.基于節點相似度的網絡社團檢測算法研究[J].計算機科學,2011,38(07):185-189.
[9]劉旭,易東云.基于局部相似性的復雜網絡社區發現方法[J].北京: 自動化學報,2011,37(12) : 1520-1528.
基金資助:河北科技大學理工學院大學生創新訓練項目(S202113409011)。

