一類(lèi)復(fù)合函數(shù)求導(dǎo)的兩種解法

□胡夢(mèng)薇

一、引言

在高職院校高等數(shù)學(xué)教學(xué)中，經(jīng)常會(huì)遇到計(jì)算有關(guān)一類(lèi)復(fù)合函數(shù)形式

y=eu(x)

(1)

的導(dǎo)數(shù)問(wèn)題，這里u(x)是初等函數(shù)，教材中最常用的方法是復(fù)合函數(shù)求導(dǎo)法則，運(yùn)用此種方法解決求導(dǎo)問(wèn)題的關(guān)鍵是要對(duì)復(fù)合函數(shù)進(jìn)行合理分層，雖然此種方法能夠解決大部分復(fù)合函數(shù)的求導(dǎo)問(wèn)題，但是對(duì)于某些復(fù)合函數(shù)分層比較復(fù)雜的情況就需要尋找簡(jiǎn)便方法。

對(duì)于(1)中的復(fù)合函數(shù)，選取通式y(tǒng)=esin(axn+b)為研究對(duì)象，發(fā)現(xiàn)學(xué)生在做題的過(guò)程中經(jīng)常由于分層不清楚的問(wèn)題，導(dǎo)致計(jì)算錯(cuò)誤。鑒于此，本文采用對(duì)數(shù)求導(dǎo)法，對(duì)數(shù)求導(dǎo)法是一種利用對(duì)數(shù)的性質(zhì)與隱函數(shù)的求導(dǎo)法則來(lái)簡(jiǎn)化導(dǎo)數(shù)計(jì)算的方法，使用這種方法來(lái)解決形如(1)式的顯函數(shù)的導(dǎo)數(shù)問(wèn)題，不僅減少了復(fù)合函數(shù)分層的麻煩，也有利于訓(xùn)練學(xué)生的思維能力，提高解題思路的靈活性。

本文推廣研究了如下形式

y=esin(axn+b)

(2)

的復(fù)合函數(shù)，這里a、b是常數(shù)，n∈R。

二、準(zhǔn)備知識(shí)

定義2.1[1]冪函數(shù)y=xa(a為任何實(shí)數(shù))；指數(shù)函數(shù)y=ax(a>0,且a≠1)；對(duì)數(shù)函數(shù)y=logax(a>0,且a≠1)；三角函數(shù)y=sinx，y=cosx，y=tanx，y=cotx，y=secx，y=cscx及反三角函數(shù)y=arcsinx，y=arccosx，y=arctanx等五類(lèi)函數(shù)統(tǒng)稱為基本初等函數(shù)。

定義2.2[1]如果一個(gè)函數(shù)可用一個(gè)式子表示，且這個(gè)式子是由常數(shù)及基本初等函數(shù)經(jīng)過(guò)有限次四則運(yùn)算與有限次復(fù)合構(gòu)成的，則這類(lèi)函數(shù)統(tǒng)稱為初等函數(shù)。

定義2.3[1]設(shè)D是平面上的一個(gè)點(diǎn)集，如果對(duì)于每一組數(shù)(x,y)(或稱點(diǎn)P(x,y))，變量z按一定規(guī)則f，都對(duì)應(yīng)著唯一一個(gè)確定的值，則稱變量z是變量x,y的二元函數(shù)，或稱為點(diǎn)P的函數(shù)，記作

z=f(x,y)或z=f(P)

x,y稱為自變量，z稱為因變量，D稱為函數(shù)z=f(x,y)的定義域。

定義2.4[2]設(shè)函數(shù)y=f(u)和u=φ(x)，且u=φ(x)的值域或部分值域包含在f(u)的定義域中，則通過(guò)u,y與x建立了對(duì)應(yīng)關(guān)系，記為y=f[φ(x)]，稱此函數(shù)是由函數(shù)y=f(u)和u=φ(x)復(fù)合而成的復(fù)合函數(shù)，其中u稱為中間變量。

定義2.5[2]在實(shí)際問(wèn)題中，有時(shí)還會(huì)遇到用一個(gè)方程表示函數(shù)關(guān)系的情形，例如方程x2+y2=a2確定著y與x之間的函數(shù)關(guān)系。一般地，由一個(gè)二元方程F(x,y)=0所確定的函數(shù)y=f(x)稱為隱函數(shù)。

定義2.6[2]設(shè)函數(shù)y=f(x)在點(diǎn)x0的某領(lǐng)域內(nèi)有定義，當(dāng)自變量x在點(diǎn)x0處有增量Δx時(shí)(點(diǎn)x0+Δx仍在該領(lǐng)域內(nèi))，相應(yīng)地函數(shù)有增量

Δy=f(x0+Δx)-f(x0)

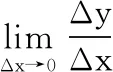
也可以記作

定義2.7[1]設(shè)函數(shù)z=f(x,y)在點(diǎn)P(x0,y0)的一個(gè)領(lǐng)域內(nèi)有定義，如果

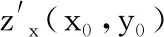
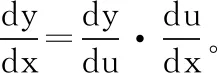
定理2.2[2](隱函數(shù)求導(dǎo))把由F(x,y)=0所確定隱函數(shù)y=y(x)代入原方程，得到恒等式

F(x,y(x))=0

運(yùn)用復(fù)合函數(shù)求導(dǎo)法，在等式兩端對(duì)x求導(dǎo)，得到一個(gè)含y′的方程，解出y′，即為所求隱函數(shù)的導(dǎo)數(shù)。

三、問(wèn)題解決的兩種方法

方法一，復(fù)合函數(shù)求導(dǎo)法[1]

解 函數(shù)y=esin(axn+b)可以看作由y=eu,u=sinv,v=axn+b復(fù)合而成，運(yùn)用復(fù)合函數(shù)求導(dǎo)法，得

一方面加強(qiáng)理論培訓(xùn)。通過(guò)培訓(xùn)讓組織者進(jìn)一步掌握中央重大決策部署，提高宣傳、團(tuán)結(jié)、發(fā)動(dòng)群眾和組織基層宣傳的能力。另一方面對(duì)組織者采取“請(qǐng)進(jìn)來(lái)、走出去”的方式提升理論素養(yǎng)、業(yè)務(wù)素質(zhì)和工作能力，有計(jì)劃分批次選派人員到機(jī)關(guān)跟班學(xué)習(xí)。

y′=(eu)′·(sinv)′·(axn+b)′

=eu·cosv·naxn-1

=naxn-1·cos(axn+b)·esin(axn+b)

因?yàn)閡和v是假設(shè)的中間變量，所以求導(dǎo)結(jié)束之后一定要記得回代，消去中間變量u和v。可以看出，運(yùn)用復(fù)合函數(shù)求導(dǎo)法對(duì)此函數(shù)進(jìn)行分層求導(dǎo)時(shí)，并且容易因?yàn)閺?fù)合函數(shù)分層的問(wèn)題而出現(xiàn)計(jì)算錯(cuò)誤，所以需要嘗試其他更簡(jiǎn)潔的方法。由于受到隱函數(shù)求導(dǎo)思想和對(duì)數(shù)函數(shù)性質(zhì)的啟發(fā)，給出下面的第二種解法。

方法二，對(duì)數(shù)求導(dǎo)法

解 等式兩邊取對(duì)數(shù)，得

lny=sin(axn+b)

方程兩邊同時(shí)對(duì)x求導(dǎo)，得

即

y′=cos(axn+b)·naxn-1·y

=naxn-1·cos(axn+b)·esin(axn+b)

通過(guò)上面的解題過(guò)程可以看出，這個(gè)方法降低了對(duì)復(fù)合函數(shù)分層的要求，減少了求導(dǎo)次數(shù)，提高了解題的正確率。

此方法的解題步驟總結(jié)如下：

(1)函數(shù)等式的兩邊取對(duì)數(shù)；

(2)等式兩邊對(duì)x求導(dǎo)，并且注意到y(tǒng)是x的函數(shù)；

(3)解出y′，并把y關(guān)于x的函數(shù)表達(dá)式代入，得到所求的結(jié)果。

上面的方法對(duì)求多元函數(shù)的偏導(dǎo)數(shù)同樣適用，我們以二元函數(shù)為例進(jìn)行說(shuō)明。

例 求函數(shù)z=esin(axn+bym)，a、b是常數(shù)，n,m∈R

解 等式兩邊取對(duì)數(shù)，得

lnz=sin(axn+bym)

方程兩邊同時(shí)對(duì)x求偏導(dǎo)，得

即

=naxn-1·cos(axn+bym)·esin(axn+bym)

四、結(jié)語(yǔ)

本文完整、詳細(xì)地研究了形如(1)式的復(fù)合函數(shù)求導(dǎo)的兩種計(jì)算方法，通過(guò)對(duì)比可以看出使用對(duì)數(shù)求導(dǎo)法計(jì)算，能夠避免因?yàn)閺?fù)合函數(shù)分層而容易出現(xiàn)的錯(cuò)誤。另外，此題的結(jié)果可以作為一個(gè)通項(xiàng)公式來(lái)用，提高此類(lèi)題目的解題效率。